经典算法的Java实现
1.快速排序描述
1.每一轮排序选择一个基准点(pivot)进行分区
1.让小于基准点的元素进入一个分区,大于基准点的元素进入另一个分区
2.当分区完成时,基准点元素的位置就是其最终位置
2.在子分区重复以上过程,直至子分区元素个数少于等于1,这体现的是分而治之的思想(divide-and-conquer)
2.单边循环快排 (lomuto 洛穆托分区方案)
1.选择最右元素作为基准点元素
2. i 指针维护小于基准点元素的边界,也是每次交换的目标索引
3. j 指针负责找到比基准点小的元素,一旦找到则与 i 进行交换
4.最后基准点与i交换,i即为分区位置
3.特点
1.平均时间复杂度是 O(n㏒ⁿ) ,最坏时间复杂度是 O(n²)
2.数据量较大时,优势非常明显
3.属于不稳定排序
/**
* 快速排序 (单边循环方法)
*/
public class QuickSort {
public static void main(String[] args) {
// 原始数据
int[] arr = {5,3,7,2,9,8,1,4};
quickSort(arr,0,arr.length - 1);
}
//快速排序方法 递归方法
public static void quickSort(int[] arr,int l,int h) {
if (l >= h) {
// 代表没有可以执行的分区退出递归
return;
}
//调用分区方法 获取每轮分组的边界
int p = partition(arr, l, h);
//左边分区的范围确定
quickSort(arr,l,p - 1);
//右边分区的范围确定
quickSort(arr,p + 1,h);
}
//分区方法
public static int partition(int[] arr ,int l,int h) {
// pv是基准点元素,h 是分区上限也是本轮分区基准点
int pv = arr[h];
// i 是交换目标索引,l 是左边界
int i = l;
// j 开始循环获取比基准点小的值
for (int j = l; j < h; j++) {
if (arr[j] < pv) {
if (i != j) {
// 如果比较的元素小于基准点,
// 并且他不是目标索引的位置,
// 就把j元素交换到目标索引位置
swap(arr,i,j);
}
// 目标索引加1
i++;
}
}
if (i != h) {
swap(arr,h,i);
}
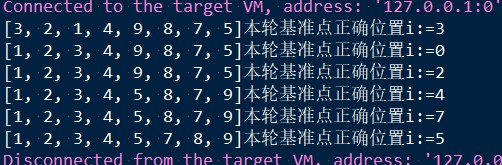
System.out.println(Arrays.toString(arr)+"本轮基准点正确位置i:="+i);
// 返回值代表基准点元素所在正确索引位置,用它确定下一轮分区的边界
return i;
}
// 交换方法
public static void swap(int[] arr,int i,int j) {
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
执行效果
1.何为选择排序:
以升序为例:
2.重复上述步骤,知道数组有序
2.优化方式
1.为减少交换次数,每一轮可以先找到最小的索引,再每轮最后交换元素的位置
3.与冒泡排序比较
1.两者的时间复杂度都为O(n²)
2.选择排序一般快于冒泡排序,因为其交换次数少
3.但如果集合有序度高,冒泡优于选择
/**
* 选择排序
*/
public class SelectSort {
public static void main(String[] args) {
// 原始数据
int[] arr = {1,4,2,7,5,8,9};
// 选择排序方法
selectSort(arr);
}
private static void selectSort(int[] arr) {
// 需要执行的轮次
for (int i = 0; i < arr.length-1; i++) {
// i 代表每轮最小元素需要交换到的索引
int s = i;
for (int j = s + 1; j < arr.length; j++) {
// 和数组每个元素比对
if (arr[s] > arr[j]) {
// 给最小元素索引赋值
s = j;
}
}
// 判断本轮最小元素是否就是本轮的索引i,如果不是说明发生了交换
if (s != i) {
swap(arr,s,i);
}
System.out.println(Arrays.toString(arr));
}
}
public static void swap(int[] arr,int i,int j) {
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
1.何为插入排序
1.将数组分为两个区域,排序区域和未排序区域,每一轮从未排序区域中取出第一个元素,插入到排序区域(需要保证顺序)
2.重复上述步骤,直到整个数组有序
2.优化方式
1.待插入元素进行比较时,遇到比自己小的元素,就代表找到了插入位置,无需进行后续比较
2.插入时可以直接移动元素,而不是交换元素
3.与选择排序比较
1.两者平均时间复杂度都是O(n²)
2.大部分情况下插入都略优于选择
3.有序集合插入的时间复杂度是O(n)
/**
* 插入排序
*/
public class InsertSort {
public static void main(String[] args) {
// 原始数据
int[] arr = {1,4,2,7,5,8,9};
// 插入排序
insertSort(arr);
}
private static void insertSort(int[] arr) {
// i代表插入元素的索引
for (int i = 1; i < arr.length; i++) {
// t代表要插入元素的值
int t = arr[i];
// j代表已排序的元素索引
int j = i - 1;
// 如果数组第一个元素也比完了就跳过比较循环
while (j >= 0) {
// 如果要插入的元素小于最后一个已排序的元素
if (t < arr[j]) {
// 最后一排元素往后移一位
arr[j + 1] = arr[j];
}else {
//如果改值没有比当前要插入元素小就跳出循环
break;
}
// 已排元素索引往前移一个,让要插入的元素继续与上一个已排元素比较
j--;
}
// 把要插入的元素插入到最后比较的元素位置
arr[j + 1] = t;
System.out.println(Arrays.toString(arr));
}
}
}
经典算法的Java实现
(1)河内塔问题:
说明:
河内之塔(Towers of Hanoi)是法国人M.Claus(Lucas)于1883年从泰国带至法国的,河内为越战时北越的首都,即现在的胡志明市;1883年法国数学家 Edouard Lucas曾提及这个故事,据说创世纪时Benares有一座波罗教塔,是由三支钻石棒(Pag)所支撑,开始时神在第一根棒上放置64个由上至下依由小至大排列的金盘(Disc),并命令僧侣将所有的金盘从第一根石棒移至第三根石棒,且搬运过程中遵守大盘子在小盘子之下的原则,若每日仅搬一个盘子,则当盘子全数搬运完毕之时,此塔将毁损,而也就是世界末日来临之时。
解法:
如果柱子标为ABC,要由A搬至C,在只有一个盘子时,就将它直接搬至C,当有两个盘子,就将B当作辅助柱。
如图所示:
事实上,若有n个盘子,则移动完毕所需之次数为2^n - 1,所以当盘数为64时,则所需次数为:264- 1 = 18446744073709551615 为5.05390248594782e+16年,也就是约5000世纪,如果对这数字没什么概念,就假设每秒钟搬一个盘子好了,也要约5850亿年左右。
实现:
//Java程序的实现
import java.io.*;
public class Hanoi {
public static void main(String args[]) throws IOException {
int n;
BufferedReader buf;
buf = new BufferedReader(new InputStreamReader(System. in ));
System.out.print("请输入盘数:");
n = Integer.parseInt(buf.readLine());
Hanoi hanoi = new Hanoi();
hanoi.move(n, 'A', 'B', 'C');
}
public void move(int n, char a, char b, char c) {
if (n == 1) System.out.println("盘 " + n + " 由 " + a + " 移至 " + c);
else {
move(n - 1, a, c, b);
System.out.println("盘 " + n + " 由 " + a + " 移至 " + c);
move(n - 1, b, a, c);
}
}
}
(2)费式数列
说明:
Fibonacci为1200年代的欧洲数学家,在他的著作中曾经提到:“若有一只免子每个月生一只小免子,一个月后小免子也开始生产。起初只有一只免子,一个月后就有两只免子,二个月后有三只免子,三个月后有五只免子(小免子投入生产)......”。
如果不太理解这个例子的话,举个图就知道了,注意新生的小免子需一个月成长期才会投入生产,类似的道理也可以用于植物的生长,这就是Fibonacci数列,一般习惯称之为费氏数列,例如以下:
1、1 、2、3、5、8、13、21、34、55、89......
解法:
依说明,我们可以将费氏数列定义为以下:
fn = fn-1 + fn-2 if n > 2
fn = 1 if n = 0, 1
实现:
//Java程序的实现:
public class Fibonacci {
public static void main(String[] args) {
int[] fib = new int[20];
fib[0] = 0;
fib[1] = 1;
for (int i = 2; i < fib.length; i++) fib[i] = fib[i - 1] + fib[i - 2];
for (int i = 0; i < fib.length; i++) System.out.print(fib[i] + " ");
System.out.println();
}
}
(3)巴斯卡(Pascal)三角形
说明:
巴斯卡(Pascal)三角形基本上就是在解 nCr ,因为三角形上的每一个数字各对应一个nCr,其中 n 为 row,而 r 为 column,如下:
0C0
1C0 1C1
2C0 2C1 2C2
3C0 3C1 3C2 3C3
4C0 4C1 4C2 4C3 4C4
对应的数据如下图所示:
解法:
巴斯卡三角形中的 nCr 可以使用以下这个公式来计算,以避免阶乘运算时的数值溢位:
nCr = [(n-r+1)*nCr-1]/r
nC0 = 1
实现:
//java实现
import java.awt.*;
import javax.swing.*;
public class Pascal extends JFrame {
public Pascal() {
setBackground(Color.white);
setTitle("巴斯卡三角形");
setSize(520, 350);
setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
setSize(700, 700);
setVisible(true);
}
private long combi(int n, int r) {
int i;
long p = 1;
for (i = 1; i <= r; i++) p = p * (n - i + 1) / i;
return p;
}
public void paint(Graphics g) {
g.setColor(Color.white);
g.clearRect(0, 0, getSize().width, getSize().height);
g.setColor(Color.red);
final int N = 12;
int n, r, t;
for (n = 0; n <= N; n++) {
for (r = 0; r <= n; r++) g.drawString(" " + combi(n, r), (N - n) * 20 + r * 40, n * 20 + 50);
}
}
public static void main(String args[]) {
Pascal frm = new Pascal();
}
}
(4)蒙地卡罗法求 PI
说明:
蒙地卡罗为摩洛哥王国之首都,该国位于法国与义大利国境,以赌博闻名。蒙地卡罗的基本原理为以乱数配合面积公式来进行解题,这种以机率来解题的方式带有赌博的意味,虽然在精确度上有所疑虑,但其解题的思考方向却是个值得学习的方式。
解法:
蒙地卡罗的解法适用于与面积有关的题目,例如求PI值或椭圆面积,这边介绍如何求PI值;假设有一个圆半径为1,所以四分之一圆面积就为PI,而包括此四分之一圆的正方形面积就为1,如下图所示:
如果随意的在正方形中投射飞标(点)好了,则这些飞标(点)有些会落于四分之一圆内,假设所投射的飞标(点)有n点,在圆内的飞标(点)有c点,则依比例来算,就会得到上图中最后的公式。
至于如何判断所产生的点落于圆内,很简单,令乱数产生X与Y两个数值,如果X^2+Y^2等于1就是落在圆内。
实现:
//java程序实现
public class PI {
public static void main(String[] args) {
final int N = 50000;
int sum = 0;
for (int i = 1; i < N; i++) {
double x = Math.random();
double y = Math.random();
if ((x * x + y * y) < 1) sum++;
}
System.out.println("PI = " + (double) 4 * sum / N);
}
}
(5)最大公因数、最小公倍数
说明:
解法:
最大公因数使用辗转相除法来求,最小公倍数则由这个公式来求:
GCD * LCM = 两数乘积
实现:
//java程序实现
import java.io.*;
public class GcdLcm {
public static int gcdOf(int m, int n) {
int r;
while (n != 0) {
r = m % n;
m = n;
n = r;
}
return m;
}
public static int lcmOf(int m, int n) {
return m * n / gcdOf(m, n);
}
public static void main(String[] args) throws IOException {
BufferedReader ln = new BufferedReader(new InputStreamReader(System. in ));
System.out.print("请输入第一个数:");
int x = Integer.parseInt(ln.readLine());
System.out.print("请输入第二个数:");
int y = Integer.parseInt(ln.readLine());
System.out.println("GCD of (" + x + "," + y + ")=" + GcdLcm.gcdOf(x, y));
System.out.println("LCM of (" + x + "," + y + ")=" + GcdLcm.lcmOf(x, y));
}
}
(6)阿姆斯壮数
说明:
在三位的整数中,例如153可以满足13 + 53 + 33 = 153,这样的数称之为Armstrong数,试写出一程式找出所有的三位数Armstrong数。
解法:
Armstrong数的寻找,其实就是在问如何将一个数字分解为个位数、十位数、百位数......,这只要使用除法与余数运算就可以了,例如输入 input为abc,则:
a = input / 100
b = (input%100) / 10
c = input % 10
实现:
//java程序实现
public class Armstrong {
public static void main(String[] args) {
System.out.println("寻找Armstrong数:");
for (int i = 100; i <= 999; i++) {
int a = i / 100;
int b = (i % 100) / 10;
int c = i % 10;
if (a * a * a + b * b * b + c * c * c == i) System.out.print(i + " ");
}
System.out.println();
}
}
(7)最大访客数
说明:
现将举行一个餐会,让访客事先填写到达时间与离开时间,为了掌握座位的数目,必须先估计不同时间的最大访客数。
解法:
这个题目看似有些复杂,其实相当简单,单就计算访客数这个目的,同时考虑同一访客的来访时间与离开时间,反而会使程式变得复杂;只要将来访时间与离开时间分开处理就可以了,假设访客 i 的来访时间为x[i],而离开时间为y[i]。
在资料输入完毕之后,将x[i]与y[i]分别进行排序(由小到大),道理很简单,只要先计算某时之前总共来访了多少访客,然后再减去某时之前的离开访客,就可以轻易的解出这个问题
实现:
//java实现
import java.io.*;
import java.util.*;
public class MaxVisit {
public static int maxGuest(int[] x, int[] y, int time) {
int num = 0;
for (int i = 0; i < x.length; i++) {
if (time > x[i]) num++;
if (time > y[i]) num--;
}
return num;
}
public static void main(String[] args) throws IOException {
BufferedReader buf = new BufferedReader(new InputStreamReader(System. in ));
System.out.println("输入来访时间与离开时间(0~24):");
System.out.println("范例:10 15");
System.out.println("输入-1结束");
java.util.ArrayList list = new ArrayList();
while (true) {
System.out.print(">>");
String input = buf.readLine();
if (input.equals("-1")) break;
list.add(input);
}
int[] x = new int[list.size()];
int[] y = new int[list.size()];
for (int i = 0; i < x.length; i++) {
String input = (String) list.get(i);
String[] strs = input.split(" ");
x[i] = Integer.parseInt(strs[0]);
y[i] = Integer.parseInt(strs[1]);
}
Arrays.sort(x);
Arrays.sort(y);
for (int time = 0; time < 25; time++) {
System.out.println(time + " 时的最大访客数:" + MaxVisit.maxGuest(x, y, time));
}
}
}
(8)洗扑克牌(乱数排列)
说明:
洗扑克牌的原理其实与乱数排列是相同的,都是将一组数字(例如1~N)打乱重新排列,只不过洗扑克牌多了一个花色判断的动作而已。
解法:
初学者通常会直接想到,随机产生1~N的乱数并将之存入阵列中,后来产生的乱数存入阵列前必须先检查阵列中是否已有重复的数字,如果有这个数就不存入,再重新产生下一个数,运气不好的话,重复的次数就会很多,程式的执行速度就很慢了,这不是一个好方法。
以1~52的乱数排列为例好了,可以将阵列先依序由1到52填入,然后使用一个回圈走访阵列,并随机产生1~52的乱数,将产生的乱数当作索引取出阵列值,并与目前阵列走访到的值相交换,如此就不用担心乱数重复的问题了,阵列走访完毕后,所有的数字也就重新排列了。
至于如何判断花色?这只是除法的问题而已,取商数判断花色,取余数判断数字,您可以直接看程式比较清楚。
实现:
//java实现
public class ShuffleCard {
public static void main(String args[]) {
final int N = 52;
int[] poker = new int[N + 1];
// 初始化阵列
for (int i = 1; i <= N; i++) poker[i] = i;
// 洗牌
for (int i = 1; i <= N; i++) {
int j = (int)(Math.random() * N);
if (j == 0) j = 1;
int tmp = poker[i];
poker[i] = poker[j];
poker[j] = tmp;
}
for (int i = 1; i <= N; i++) {
// 判断花色
switch ((poker[i] - 1) / 13) {
case 0:
System.out.print("桃");
break;
case 1:
System.out.print("心");
break;
case 2:
System.out.print("砖");
break;
case 3:
System.out.print("梅");
break;
}
// 扑克牌数字
int remain = poker[i] % 13;
switch (remain) {
case 0:
System.out.print("K ");
break;
case 12:
System.out.print("Q ");
break;
case 11:
System.out.print("J ");
break;
default:
System.out.print(remain + " ");
break;
}
if (i % 13 == 0) System.out.println("");
}
}
}
(9)约瑟夫问题(Josephus Problem)
说明:
据说着名犹太历史学家 Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人 开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。
然而Josephus 和他的朋友并不想遵从,Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
解法:
约瑟夫问题可用代数分析来求解,将这个问题扩大好了,假设现在您与m个朋友不幸参与了这个游戏,您要如何保护您与您的朋友?只要画两个圆圈就可以让自己与朋友免于死亡游戏,这两个圆圈内圈是排列顺序,而外圈是自杀顺序,如下图所示:
使用程式来求解的话,只要将阵列当作环状来处理就可以了,在阵列中由计数1开始,每找到三个无资料区就填入一个计数,直而计数达41为止,然后将阵列由索引1开始列出,就可以得知每个位置的自杀顺序,这就是约瑟夫排列,41个人而报数3的约琴夫排列如下所示:
14 36 1 38 15 2 24 30 3 16 34 4 25 17 5 40 31 6 18 26 7 37 19 8 35 27 9 20 32 10 41 21 11 28 39 12 22 33 13 29 23
由上可知,最后一个自杀的是在第31个位置,而倒数第二个自杀的要排在第16个位置,之前的人都死光了,所以他们也就不知道约琴夫与他的朋友并没有遵守游戏规则了。
实现:
//java实现
public class Josephus {
public static int[] arrayOfJosephus(int number, int per) {
int[] man = new int[number];
for (int count = 1, i = 0, pos = -1; count <= number; count++) {
do {
pos = (pos + 1) % number; // 环状处理
if (man[pos] == 0) i++;
if (i == per) { // 报数为3了
i = 0;
break;
}
} while (true);
man[pos] = count;
}
return man;
}
public static void main(String[] args) {
int[] man = Josephus.arrayOfJosephus(41, 3);
int alive = 3;
System.out.println("约琴夫排列:");
for (int i = 0; i < 41; i++) System.out.print(man[i] + " ");
System.out.println("\nL表示3个存活的人要放的位置:");
for (int i = 0; i < 41; i++) {
if (man[i] > (41 - alive)) System.out.print("L");
else System.out.print("D");
if ((i + 1) % 5 == 0) System.out.print(" ");
}
System.out.println();
}
}
(10)排列组合
说明:
将一组数字、字母或符号进行排列,以得到不同的组合顺序,例如1 2 3这三个数的排列组合有:1 2 3、1 3 2、2 1 3、2 3 1、3 1 2、3 2 1。
解法:
可以使用递回将问题切割为较小的单元进行排列组合,例如1 2 3 4的排列可以分为1 [2 3 4]、2 [1 3 4]、3 [1 2 4]、4 [1 2 3]进行排列,这边利用旋转法,先将旋转间隔设为0,将最右边的数字旋转至最左边,并逐步增加旋转的间隔,例如:
1 2 3 4 -> 旋转1 -> 继续将右边2 3 4进行递回处理
2 1 3 4 -> 旋转1 2 变为 2 1-> 继续将右边1 3 4进行递回处理
3 1 2 4 -> 旋转1 2 3变为 3 1 2 -> 继续将右边1 2 4进行递回处理
4 1 2 3 -> 旋转1 2 3 4变为4 1 2 3 -> 继续将右边1 2 3进行递回处理
实现:
//java实现
public class Permutation {
public static void perm(int[] num, int i) {
if (i < num.length - 1) {
for (int j = i; j <= num.length - 1; j++) {
int tmp = num[j];
// 旋转该区段最右边数字至最左边
for (int k = j; k > i; k--) num[k] = num[k - 1];
num[i] = tmp;
perm(num, i + 1);
// 还原
for (int k = i; k < j; k++) num[k] = num[k + 1];
num[j] = tmp;
}
} else {
// 显示此次排列
for (int j = 1; j <= num.length - 1; j++) System.out.print(num[j] + " ");
System.out.println();
}
}
public static void main(String[] args) {
int[] num = new int[4 + 1];
for (int i = 1; i <= num.length - 1; i++) num[i] = i;
perm(num, 1);
}
}
(11)得分排行
说明:
假设有一教师依学生座号输入考试分数,现希望在输入完毕后自动显示学生分数的排行,当然学生的分数可能相同。
解法:
这个问题基本上要解不难,只要使用额外的一个排行阵列走访分数阵列就可以了,直接使用下面的程式片段作说明:
for(i = 0; i < count; i++) {
juni[i] = 1;
for(j = 0; j < count; j++) {
if(score[j] > score[i])
juni[i]++;
}
}
printf("得分\t排行\n");
for(i = 0; i < count; i++)
printf("%d\t%d\n", score[i], juni[i]);
上面这个方法虽然简单,但是反覆计算的次数是n^2,如果n值变大,那么运算的时间就会拖长;改变juni阵列的长度为n+2,并将初始值设定为0,如下所示:
接下来走访分数阵列,并在分数所对应的排行阵列索引元素上加1,如下所示:
将排行阵列最右边的元素设定为1,然后依序将右边的元素值加至左边一个元素,最后排行阵列中的「分数+1」」就是得该分数的排行,如下所示:
这样的方式看起来复杂,其实不过在计算某分数之前排行的人数,假设89分之前的排行人数为x人,则89分自然就是x+1了,这也是为什么排行阵列最右边要设定为1的原因;如果89分有y人,则88分自然就是x+y+1,整个阵列右边元素向左加的原因正是如此。
如果分数有负分的情况,由于C/C++或Java等程式语言无法处理负的索引,所以必须加上一个偏移值,将所有的分数先往右偏移一个范围即可,最后显示的时候记得减回偏移值就可以了。
实现:
//
import java.io.*;
public class ScoreRank {
public static void main(String[] args)
throws NumberFormatException, IOException {
final int MAX = 100;
final int MIN = 0;
int[] score = new int[MAX + 1];
int[] juni = new int[MAX + 2];
BufferedReader reader = new BufferedReader(new InputStreamReader(System. in ));
int count = 0;
do {
System.out.print("输入分数,-1结束:");
score[count++] = Integer.parseInt(reader.readLine());
} while ((score[count - 1] != -1));
count--;
for (int i = 0; i < count; i++) juni[score[i]]++;
juni[MAX + 1] = 1;
for (int i = MAX; i >= MIN; i--) juni[i] = juni[i] + juni[i + 1];
System.out.println("得分\t排行");
for (int i = 0; i < count; i++) {
System.out.println(score[i] + "\t" + juni[score[i] + 1]);
}
}
}
(12)选择、插入、气泡排序
说明:
选择排序(Selection sort)、插入排序(Insertion sort)与气泡排序(Bubble sort)这三个排序方式是初学排序所必须知道的三个基本排序方式,它们由于速度不快而不实用(平均与最快的时间复杂度都是O(n2)),然而它们排序的方式确是值得观察与探讨的。
解法:
① 选择排序
将要排序的对象分作两部份,一个是已排序的,一个是未排序的,从后端未排序部份选择一个最小值,并放入前端已排序部份的最后一个,例如:
排序前:70 80 31 37 10 1 48 60 33 80
[1] 80 31 37 10 70 48 60 33 80 选出最小值1
[1 10] 31 37 80 70 48 60 33 80 选出最小值10
[1 10 31] 37 80 70 48 60 33 80 选出最小值31
[1 10 31 33] 80 70 48 60 37 80 ......
[1 10 31 33 37] 70 48 60 80 80 ......
[1 10 31 33 37 48] 70 60 80 80 ......
[1 10 31 33 37 48 60] 70 80 80 ......
[1 10 31 33 37 48 60 70] 80 80 ......
[1 10 31 33 37 48 60 70 80] 80 ......
② 插入排序
像是玩朴克一样,我们将牌分作两堆,每次从后面一堆的牌抽出最前端的牌,然后插入前面一堆牌的适当位置,例如:
排序前:92 77 67 8 6 84 55 85 43 67
[77 92] 67 8 6 84 55 85 43 67 将77插入92前
[67 77 92] 8 6 84 55 85 43 67 将67插入77前
[8 67 77 92] 6 84 55 85 43 67 将8插入67前
[6 8 67 77 92] 84 55 85 43 67 将6插入8前
[6 8 67 77 84 92] 55 85 43 67 将84插入92前
[6 8 55 67 77 84 92] 85 43 67 将55插入67前
[6 8 55 67 77 84 85 92] 43 67 ......
[6 8 43 55 67 77 84 85 92] 67 ......
[6 8 43 55 67 67 77 84 85 92] ......
③ 气泡排序法
顾名思义,就是排序时,最大的元素会如同气泡一样移至右端,其利用比较相邻元素的方法,将大的元素交换至右端,所以大的元素会不断的往右移动,直到适当的位置为止。
基本的气泡排序法可以利用旗标的方式稍微减少一些比较的时间,当寻访完阵列后都没有发生任何的交换动作,表示排序已经完成,而无需再进行之后的回圈比较与交换动作,例如:
排序前:95 27 90 49 80 58 6 9 18 50
27 90 49 80 58 6 9 18 50 [95] 95浮出
27 49 80 58 6 9 18 50 [90 95] 90浮出
27 49 58 6 9 18 50 [80 90 95] 80浮出
27 49 6 9 18 50 [58 80 90 95] ......
27 6 9 18 49 [50 58 80 90 95] ......
6 9 18 27 [49 50 58 80 90 95] ......
6 9 18 [27 49 50 58 80 90 95] 由于接下来不会再发生交换动作,排序提早结束
在上面的例子当中,还加入了一个观念,就是当进行至i与i+1时没有交换的动作,表示接下来的i+2至n已经排序完毕,这也增进了气泡排序的效率。
实现:
//Java程序实现
public class BasicSort {
public static void selectionSort(int[] number) {
for (int i = 0; i < number.length - 1; i++) {》》
int m = i;
for (int j = i + 1; j < number.length; j++)
if (number[j] < number[m]) m = j; === = if (i != m) swap(number, i, m);
}
}
public static void injectionSort(int[] number) {
for (int j = 1; j < number.length; j++) {
int tmp = number[j];
int i = j - 1;
while (tmp < number[i]) {
number[i + 1] = number[i];
i--;
if (i == -1) break;
}
number[i + 1] = tmp;
}
}
public static void bubbleSort(int[] number) {
boolean flag = true;
for (int i = 0; i < number.length - 1 && flag; i++) {
flag = false;
for (int j = 0; j < number.length - i - 1; j++) {
if (number[j + 1] < number[j]) {
swap(number, j + 1, j);
flag = true;
}
}
}
}
private static void swap(int[] number, int i, int j) {
int t;
t = number[i];
number[i] = number[j];
number[j] = t;
}
public static void main(String[] args) {
//测试:
int[] a = {
10, 9, 1, 100, 20, 200, 39, 45, 23, 18, 2, 2, 15
};
//测试选择排序:
System.out.println("选择排序前:");
for (int x: a) System.out.print(x + " ");
System.out.println();
int[] b = new int[a.length];
b = a;
selectionSort(b);
System.out.println("选择排序后:");
for (int x: b) System.out.print(x + " ");
System.out.println();
//测试插入排序:
System.out.println("插入排序前:");
for (int x: a) System.out.print(x + " ");
System.out.println();
int[] c = new int[a.length];
c = a;
injectionSort(c);
System.out.println("插入排序后:");
for (int x: c) System.out.print(x + " ");
System.out.println();
//测试气泡排序:
System.out.println("气泡排序前:");
for (int x: a) System.out.print(x + " ");
System.out.println();
int[] d = new int[a.length];
d = a;
bubbleSort(d);
System.out.println("气泡排序后:");
for (int x: d) System.out.print(x + " ");
}
}
(13)快速排序(一)
说明:
快速排序法(quick sort)是目前所公认最快的排序方法之一(视解题的对象而定),虽然快速排序法在最差状况下可以达O(n2),但是在多数的情况下,快速排序法的效率表现是相当不错的。
快速排序法的基本精神是在数列中找出适当的轴心,然后将数列一分为二,分别对左边与右边数列进行排序,而影响快速排序法效率的正是轴心的选择。
这边所介绍的第一个快速排序法版本,是在多数的教科书上所提及的版本,因为它最容易理解,也最符合轴心分割与左右进行排序的概念,适合对初学者进行讲解。
解法:
这边所介绍的快速演算如下:将最左边的数设定为轴,并记录其值为 s
廻圈处理:
令索引 i 从数列左方往右方找,直到找到大于 s 的数
令索引 j 从数列左右方往左方找,直到找到小于 s 的数
如果 i >= j,则离开回圈
如果 i < j,则交换索引i与j两处的值
将左侧的轴与 j 进行交换
对轴左边进行递回
对轴右边进行递回
透过以下演算法,则轴左边的值都会小于s,轴右边的值都会大于s,如此再对轴左右两边进行递回,就可以对完成排序的目的,例如下面的实例,*表示要交换的数,[]表示轴:
[41] 24 76* 11 45 64 21 69 19 36*
[41] 24 36 11 45* 64 21 69 19* 76
[41] 24 36 11 19 64* 21* 69 45 76
[41] 24 36 11 19 21 64 69 45 76
21 24 36 11 19 [41] 64 69 45 76
在上面的例子中,41左边的值都比它小,而右边的值都比它大,如此左右再进行递回至排序完成。
实现:
//java实现
public class QuickSort {
public static void sort(int[] number) {
sort(number, 0, number.length - 1);
}
private static void sort(int[] number, int left, int right) {
if (left < right) {
int s = number[left];
int i = left;
int j = right + 1;
while (true) {
// 向右找
while (i + 1 < number.length && number[++i] < s);
// 向左找
while (j - 1 > -1 && number[--j] > s);
if (i >= j) break;
swap(number, i, j);
}
number[left] = number[j];
number[j] = s;
sort(number, left, j - 1);
// 对左边进行递回
sort(number, j + 1, right);
// 对右边进行递回
}
}
private static void swap(int[] number, int i, int j) {
int t;
t = number[i];
number[i] = number[j];
number[j] = t;
}
}
(14)快速排序(二)
说明:
在快速排序法(一)中,每次将最左边的元素设为轴,而之前曾经说过,快速排序法的加速在于轴的选择,在这个例子中,只将轴设定为中间的元素,依这个元素作基准进行比较,这可以增加快速排序法的效率。
解法:
在这个例子中,取中间的元素s作比较,同样的先得右找比s大的索引 i,然后找比s小的索引 j,只要两边的索引还没有交会,就交换 i 与 j 的元素值,这次不用再进行轴的交换了,因为在寻找交换的过程中,轴位置的元素也会参与交换的动作,例如:
41 24 76 11 45 64 21 69 19 36
首先left为0,right为9,(left+right)/2 = 4(取整数的商),所以轴为索引4的位置,比较的元素是45,您往右找比45大的,往左找比45小的进行交换:
41 24 76* 11 [45] 64 21 69 19 *36
41 24 36 11 45* 64 21 69 19* 76
41 24 36 11 19 64* 21* 69 45 76
[41 24 36 11 19 21] [64 69 45 76]
完成以上之后,再初别对左边括号与右边括号的部份进行递回,如此就可以完成排序的目的。
实现:
public class QuickSort {
public static void sort(int[] number) {
sort(number, 0, number.length - 1);
}
private static void sort(int[] number, int left, int right) {
if (left < right) {
int s = number[(left + right) / 2];
int i = left - 1;
int j = right + 1;
while (true) {
// 向右找
while (number[++i] < s);
// 向左找
while (number[--j] > s);
if (i >= j) break;
swap(number, i, j);
}
sort(number, left, i - 1);
// 对左边进行递回
sort(number, j + 1, right);
// 对右边进行递回
}
}
private static void swap(int[] number, int i, int j) {
int t;
t = number[i];
number[i] = number[j];
number[j] = t;
}
}
(15)快速排序(三)
说明:
之前说过轴的选择是快速排序法的效率关键之一,在这边的快速排序法的轴选择方式更加快了快速排序法的效率,它是来自演算法名书 Introduction to Algorithms 之中。
解法:
先说明这个快速排序法的概念,它以最右边的值s作比较的标准,将整个数列分为三个部份,一个是小于s的部份,一个是大于s的部份,一个是未处理的部份,如下所示 :
在排序的过程中,i 与 j 都会不断的往右进行比较与交换,最后数列会变为以下的状态:
然后将s的值置于中间,接下来就以相同的步骤会左右两边的数列进行排序的动作,如下所示:
整个演算的过程,直接摘录书中的虚拟码来作说明:
实现:
public class QuickSort3 {
public static void sort(int[] number) {
sort(number, 0, number.length - 1);
}
private static void sort(int[] number, int left, int right) {
if (left < right) {
int q = partition(number, left, right);
sort(number, left, q - 1);
sort(number, q + 1, right);
}
}
private static int partition(int number[], int left, int right) {
int s = number[right];
int i = left - 1;
for (int j = left; j < right; j++) {
if (number[j] <= s) {
i++;
swap(number, i, j);
}
}
swap(number, i + 1, right);
return i + 1;
}
private static void swap(int[] number, int i, int j) {
int t;
t = number[i];
number[i] = number[j];
number[j] = t;
}
}
(16)合并排序
说明:
之前所介绍的排序法都是在同一个阵列中的排序,考虑今日有两笔或两笔以上的资料,它可能是不同阵列中的资料,或是不同档案中的资料,如何为它们进行排序?
解法:
可以使用合并排序法,合并排序法基本是将两笔已排序的资料合并并进行排序,如果所读入的资料尚未排序,可以先利用其它的排序方式来处理这两笔资料,然后再将排序好的这两笔资料合并。
有人问道,如果两笔资料本身就无排序顺序,何不将所有的资料读入,再一次进行排序?排序的精神是尽量利用资料已排序的部份,来加快排序的效率,小笔资料的排序较为快速,如果小笔资料排序完成之后,再合并处理时,因为两笔资料都有排序了,所有在合并排序时会比单纯读入所有的资料再一次排序来的有效率。
那么可不可以直接使用合并排序法本身来处理整个排序的动作?而不动用到其它的排序方式?答案是肯定的,只要将所有的数字不断的分为两个等分,直到最后剩一个数字为止,然后再反过来不断的合并,就如下图所示:
不过基本上分割又会花去额外的时间,不如使用其它较好的排序法来排序小笔资料,再使用合并排序来的有效率。
实现:
public class MergeSort {
public static int[] sort(int[] number1, int[] number2) {
int[] number3 = new int[number1.length + number2.length];
int i = 0, j = 0, k = 0;
while (i < number1.length && j < number2.length) {
if (number1[i] <= number2[j]) number3[k++] = number1[i++];
else number3[k++] = number2[j++];
}
while (i < number1.length) number3[k++] = number1[i++];
while (j < number2.length) number3[k++] = number2[j++];
return number3;
}
}
(17)基数排序
说明:
在之前所介绍过的排序方法,都是属于「比较性」的排序法,也就是每次排序时 ,都是比较整个键值的大小以进行排序。
这边所要介绍的「基数排序法」(radix sort)则是属于「分配式排序」(distribution sort),基数排序法又称「桶子法」(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些「桶」中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的比较性排序法。
解法:
基数排序的方式可以采用LSD(Least sgnificant digital)或MSD(Most sgnificant digital),LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
以LSD为例,假设原来有一串数值如下所示:
73, 22, 93, 43, 55, 14, 28, 65, 39, 81
首先根据个位数的数值,在走访数值时将它们分配至编号0到9的桶子中:
0
1
2
3
4
5
6
7
8
9
81
65
39
43
14
55
28
93
22
73
接下来将这些桶子中的数值重新串接起来,成为以下的数列:
81, 22, 73, 93, 43, 14, 55, 65, 28, 39
接着再进行一次分配,这次是根据十位数来分配:
0
1
2
3
4
5
6
7
8
9
28
39
14
22
43
55
65
73
81
93
接下来将这些桶子中的数值重新串接起来,成为以下的数列:
14, 22, 28, 39, 43, 55, 65, 73, 81, 93
这时候整个数列已经排序完毕;如果排序的对象有三位数以上,则持续进行以上的动作直至最高位数为止。
LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好,MSD的方式恰与LSD相反,是由高位数为基底开始进行分配,其他的演 算方式则都相同。
实现:
public class RadixSort {
public static void sort(int[] number, int d) {
int k = 0;
int n = 1;
int[][] temp = new int[number.length][number.length];
int[] order = new int[number.length];
while (n <= d) {
for (int i = 0; i < number.length; i++) {
int lsd = ((number[i] / n) % 10);
temp[lsd][order[lsd]] = number[i];
order[lsd]++;
}
for (int i = 0; i < number.length; i++) {
if (order[i] != 0)
for (int j = 0; j < order[i]; j++) {
number[k] = temp[i][j];
k++;
}
order[i] = 0;
}
n *= 10;
k = 0;
}
}
public static void main(String[] args) {
int[] data = {
73, 22, 93, 43, 55, 14, 28, 65, 39, 81, 33, 100
};
RadixSort.sort(data, 100);
for (int i = 0; i < data.length; i++) {
System.out.print(data[i] + " ");
}
}
}
(18)循序查找法(使用卫兵)
说明:
搜寻的目的,是在「已排序的资料」中寻找指定的资料,而当中循序搜寻是最基本的搜寻法,只要从资料开头寻找到最后,看看是否找到资料即可。
解法:
初学者看到循序搜寻,多数都会使用以下的方式来进行搜寻:
while(i < MAX) {
if(number[i] == k) {
printf("找到指定值");
break;
}
i++;
}
这个方法基本上没有错,但是可以加以改善,可以利用设定卫兵的方式,省去if判断式,卫兵通常设定在数列最后或是最前方,假设设定在列前方好了(索引0的 位置),我们从数列后方向前找,如果找到指定的资料时,其索引值不是0,表示在数列走访完之前就找到了,在程式的撰写上,只要使用一个while回圈就可 以了。
实现:
public class LinearSearch {
public static int search(int[] number, int des) {
int[] tmp = new int[number.length + 1];
for (int i = 1; i < tmp.length; i++) {
tmp[i] = number[i - 1];
}
tmp[0] = des;
int k = tmp[0];
int i = number.length;
while (tmp[i] != k) i--;
return i - 1;
}
public static void main(String[] args) {
int[] number = {
1, 4, 2, 6, 7, 3, 9, 8
};
QuickSort.sort(number);
int find = LinearSearch.search(number, 3);
if (find != 0) System.out.println("找到数值于索引" + find);
else System.out.println("找不到数值");
}
}
(19)二分查找法
说明:
如果搜寻的数列已经有排序,应该尽量利用它们已排序的特性,以减少搜寻比对的次数,这是搜寻的基本原则,二分搜寻法是这个基本原则的代表。
解法:
在二分搜寻法中,从数列的中间开始搜寻,如果这个数小于我们所搜寻的数,由于数列已排序,则该数左边的数一定都小于要搜寻的对象,所以无需浪费时间在左边的数;如果搜寻的数大于所搜寻的对象,则右边的数无需再搜寻,直接搜寻左边的数。
所以在二分搜寻法中,将数列不断的分为两个部份,每次从分割的部份中取中间数比对,例如要搜寻92于以下的数列,首先中间数索引为(0+9)/2 = 4(索引由0开始):
[3 24 57 57 67 68 83 90 92 95]
由于67小于92,所以转搜寻右边的数列:
3 24 57 57 67 [68 83 90 92 95]
由于90小于92,再搜寻右边的数列,这次就找到所要的数了:
3 24 57 57 67 68 83 90 [92 95]
实现:
public class BinarySearch {
public static int search(int[] number, int des) {
int low = 0;
int upper = number.length - 1;
while (low <= upper) {
int mid = (low + upper) / 2;
if (number[mid] < des) low = mid + 1;
else if (number[mid] > des) upper = mid - 1;
else return mid;
}
return -1;
}
public static void main(String[] args) {
int[] number = {
1, 4, 2, 6, 7, 3, 9, 8
};
QuickSort.sort(number);
int find = BinarySearch.search(number, 3);
if (find != -1) System.out.println("找到数值于索引" + find);
else System.out.println("找不到数值");
}
}
(20)插补查找法
说明:
如果却搜寻的资料分布平均的话,可以使用插补(Interpolation)搜寻法来进行搜寻,在搜寻的对象大于500时,插补搜寻法会比 二分搜寻法 来的快速。
解法:
插补搜寻法是以资料分布的近似直线来作比例运算,以求出中间的索引并进行资料比对,如果取出的值小于要寻找的值,则提高下界,如果取出的值大于要寻找的值,则降低下界,如此不断的减少搜寻的范围,所以其本原则与二分搜寻法是相同的,至于中间值的寻找是透过比例运算,如下所示,其中K是指定要寻找的对象, 而m则是可能的索引值:
实现:
public class InterpolationSearch {
public static int search(int[] number, int des) {
int low = 0;
int upper = number.length - 1;
while (low <= upper) {
int mid = (upper - low) * (des - number[low]) / (number[upper] - number[low]) + low;
if (mid < low || mid > upper) return -1;
if (des < number[mid]) upper = mid - 1;
else if (des > number[mid]) low = mid + 1;
else return mid;
}
return -1;
}
public static void main(String[] args) {
int[] number = {
1, 4, 2, 6, 7, 3, 9, 8
};
QuickSort.sort(number);
int find = InterpolationSearch.search(number, 3);
if (find != -1) System.out.println("找到数值于索引" + find);
else System.out.println("找不到数值");
}
}
(21)费式查找法
说明:
二分搜寻法每次搜寻时,都会将搜寻区间分为一半,所以其搜寻时间为O(log(2)n),log(2)表示以2为底的log值,这边要介绍的费氏搜寻,其利用费氏数列作为间隔来搜寻下一个数,所以区间收敛的速度更快,搜寻时间为O(logn)。
解法:
费氏搜寻使用费氏数列来决定下一个数的搜寻位置,所以必须先制作费氏数列,这在之前有提过;费氏搜寻会先透过公式计算求出第一个要搜寻数的位置,以及其代表的费氏数,以搜寻对象10个数字来说,第一个费氏数经计算后一定是F5,而第一个要搜寻的位置有两个可能,例如若在下面的数列搜寻的话(为了计算方便, 通常会将索引0订作无限小的数,而数列由索引1开始):
-infin; 1 3 5 7 9 13 15 17 19 20
如果要搜寻5的话,则由索引F5 = 5开始搜寻,接下来如果数列中的数小于指定搜寻值时,就往左找,大于时就向右,每次找的间隔是F4、F3、F2来寻找,当费氏数为0时还没找到,就表示寻找失败,如下所示:
由于第一个搜寻值索引F5 = 5处的值小于19,所以此时必须对齐数列右方,也就是将第一个搜寻值的索引改为F5+2 = 7,然后如同上述的方式进行搜寻,如下所示:
至于第一个搜寻值是如何找到的?我们可以由以下这个公式来求得,其中n为搜寻对象的个数:
Fx + m = n
Fx <= n
也就是说Fx必须找到不大于n的费氏数,以10个搜寻对象来说:
Fx + m = 10
取Fx = 8, m = 2,所以我们可以对照费氏数列得x = 6,然而第一个数的可能位置之一并不是F6,而是第x-1的费氏数,也就是F5 = 5。
如果数列number在索引5处的值小于指定的搜寻值,则第一个搜寻位置就是索引5的位置,如果大于指定的搜寻值,则第一个搜寻位置必须加上m,也就是F5 + m = 5 + 2 = 7,也就是索引7的位置,其实加上m的原因,是为了要让下一个搜寻值刚好是数列的最后一个位置。
费氏搜寻看来难懂,但只要掌握Fx + m = n这个公式,自己找几个实例算一次,很容易就可以理解;费氏搜寻除了收敛快速之外,由于其本身只会使用到加法与减法,在运算上也可以加快。
实现:
public class FibonacciSearch {
public static int search(int[] number, int des) {
int[] fib = createFibonacci(number.length);
int x = findX(fib, number.length + 1, des);
int m = number.length - fib[x];
x--;
int i = x;
if (number[i] < des) i += m;
while (fib[x] > 0) {
if (number[i] < des) i += fib[--x];
else if (number[i] > des) i -= fib[--x];
else return i;
}
return -1;
}
private static int[] createFibonacci(int max) {
int[] fib = new int[max];
for (int i = 0; i < fib.length; i++) {
fib[i] = Integer.MIN_VALUE;
}
fib[0] = 0;
fib[1] = 1;
for (int i = 2; i < max; i++) fib[i] = fib[i - 1] + fib[i - 2];
return fib;
}
private static int findX(int[] fib, int n, int des) {
int i = 0;
while (fib[i] <= n) i++;
i--;
return i;
}
public static void main(String[] args) {
int[] number = {
1, 4, 2, 6, 7, 3, 9, 8
};
QuickSort.sort(number);
int find = FibonacciSearch.search(number, 3);
if (find != -1) System.out.println("找到数值于索引" + find);
else System.out.println("找不到数值");
}
}
(22)稀疏矩阵
说明:
如果在矩阵中,多数的元素并没有资料,称此矩阵为稀疏矩阵(sparse matrix),由于矩阵在程式中常使用二维阵列表示,二维阵列的大小与使用的记忆体空间成正比,如果多数的元素没有资料,则会造成记忆体空间的浪费,为 此,必须设计稀疏矩阵的阵列储存方式,利用较少的记忆体空间储存完整的矩阵资讯。
解法:
在这边所介绍的方法较为简单,阵列只储存矩阵的行数、列数与有资料的索引位置及其值,在需要使用矩阵资料时,再透过程式运算加以还原,例如若矩阵资料如下,其中0表示矩阵中该位置没有资料:
0 0 0 0 0 0
0 3 0 0 0 0
0 0 0 6 0 0
0 0 9 0 0 0
0 0 0 0 12 0
这个矩阵是5X6矩阵,非零元素有4个,您要使用的阵列第一列记录其列数、行数与非零元素个数:
5 6 4
阵列的第二列起,记录其位置的列索引、行索引与储存值:
1 1 3
2 3 6
3 2 9
4 4 12
所以原本要用30个元素储存的矩阵资讯,现在只使用了15个元素来储存,节省了不少记忆体的使用。
实现:
public class SparseMatrix {
public static int[][] restore(int[][] sparse) {
int row = sparse[0][0];
int column = sparse[0][1];
int[][] array = new int[row][column];
int k = 1;
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
if (k <= sparse[0][2] && i == sparse[k][0] && j == sparse[k][1]) {
array[i][j] = sparse[k][2];
k++;
} else array[i][j] = 0;
}
}
return array;
}
public static void main(String[] args) {
int[][] sparse = {
{
5, 6, 4
}, {
1, 1, 3
}, {
2, 3, 6
}, {
3, 2, 9
}, {
4, 4, 12
}
};
int[][] array = SparseMatrix.restore(sparse);
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}
}
}
(23)多维矩阵转一维矩阵
说明:
有的时候,为了运算方便或资料储存的空间问题,使用一维阵列会比二维或多维阵列来得方便,例如上三角矩阵、下三角矩阵或对角矩阵,使用一维阵列会比使用二维阵列来得节省空间。
解法:
以二维阵列转一维阵列为例,索引值由0开始,在由二维阵列转一维阵列时,我们有两种方式:「以列(Row)为主」或「以行(Column)为主」。由于 C/C++、Java等的记忆体配置方式都是以列为主,所以您可能会比较熟悉前者(Fortran的记忆体配置方式是以行为主)。
以列为主的二维阵列要转为一维阵列时,是将二维阵列由上往下一列一列读入一维阵列,此时索引的对应公式如下所示,其中row与column是二维阵列索引,loc表示对应的一维阵列索引:
loc = column + row*行数
以行为主的二维阵列要转为一维阵列时,是将二维阵列由左往右一行一行读入一维阵列,此时索引的对应公式如下所示:
loc = row + column*列数
公式的推导您画图看看就知道了,如果是三维阵列,则公式如下所示,其中i(个数u1)、j(个数u2)、k(个数u3)分别表示三维阵列的三个索引:
以列为主:loc = i*u2*u3 + j*u3 + k
以行为主:loc = k*u1*u2 + j*u1 + i
更高维度的可以自行依此类推,但通常更高维度的建议使用其它资料结构(例如物件包装)会比较具体,也不易搞错。
实现:
public class TwoDimArray {
public static int[] toOneDimByRow(int[][] array) {
int[] arr = new int[array.length * array[0].length];
for (int row = 0; row < array.length; row++) {
for (int column = 0; column < array[0].length; column++) {
int i = column + row * array[0].length;
arr[i] = array[row][column];
}
}
return arr;
}
public static int[] toOneDimByColumn(int[][] array) {
int[] arr = new int[array.length * array[0].length];
for (int row = 0; row < array.length; row++) {
for (int column = 0; column < array[0].length; column++) {
int i = i = row + column * array.length;
arr[i] = array[row][column];
}
}
return arr;
}
}
(24)上三角、下三角、对称矩阵
说明:
上三角矩阵是矩阵在对角线以下的元素均为0,即Aij = 0,i > j,例如:
1 2 3 4 5
0 6 7 8 9
0 0 10 11 12
0 0 0 13 14
0 0 0 0 15
下三角矩阵是矩阵在对角线以上的元素均为0,即Aij = 0,i < j,例如:
1 0 0 0 0
2 6 0 0 0
3 7 10 0 0
4 8 11 13 0
5 9 12 14 15
对称矩阵是矩阵元素对称于对角线,例如:
1 2 3 4 5
2 6 7 8 9
3 7 10 11 12
4 8 11 13 14
5 9 12 14 15
上三角或下三角矩阵也有大部份的元素不储存值(为0),我们可以将它们使用一维阵列来储存以节省储存空间,而对称矩阵因为对称于对角线,所以可以视为上三角或下三角矩阵来储存。
解法:
假设矩阵为nxn,为了计算方便,我们让阵列索引由1开始,上三角矩阵化为一维阵列,若以列为主,其公式为:loc = n*(i-1) - i*(i-1)/2 + j
化为以行为主,其公式为:loc = j*(j-1)/2 + i
下三角矩阵化为一维阵列,若以列为主,其公式为:loc = i*(i-1)/2 + j
若以行为主,其公式为:loc = n*(j-1) - j*(j-1)/2 + i
实现:
public class TriangleArray {
private int[] arr;
private int length;
public TriangleArray(int[][] array) {
length = array.length;
arr = new int[length * (1 + length) / 2];
int loc = 0;
for (int i = 0; i < length; i++) {
for (int j = 0; j < length; j++) {
if (array[i][j] != 0) arr[loc++] = array[i][j];
}
}
}
public int getValue(int i, int j) {
int loc = length * i - i * (i + 1) / 2 + j;
return arr[loc];
}
public static void main(String[] args) {
int[][] array = {
{
1, 2, 3, 4, 5
}, {
0, 6, 7, 8, 9
}, {
0, 0, 10, 11, 12
}, {
0, 0, 0, 13, 14
}, {
0, 0, 0, 0, 15
}
};
TriangleArray triangleArray = new TriangleArray(array);
System.out.print(triangleArray.getValue(2, 2));
}
}
(25)奇数魔方阵
说明:
将1到n(为奇数)的数字排列在nxn的方阵上,且各行、各列与各对角线的和必须相同,如下所示:
解法:
填魔术方阵的方法以奇数最为简单,第一个数字放在第一行第一列的正中央,然后向右(左)上填,如果右(左)上已有数字,则向下填,如下图所示:
一般程式语言的阵列索引多由0开始,为了计算方便,我们利用索引1到n的部份,而在计算是向右(左)上或向下时,我们可以将索引值除以n值,如果得到余数为1就向下,否则就往右(左)上,原理很简单,看看是不是已经在同一列上绕一圈就对了。
实现:
public class Matrix {
public static int[][] magicOdd(int n) {
int[][] square = new int[n + 1][n + 1];
int i = 0;
int j = (n + 1) / 2;
for (int key = 1; key <= n * n; key++) {
if ((key % n) == 1) i++;
else {
i--;
j++;
}
if (i == 0) i = n;
if (j > n) j = 1;
square[i][j] = key;
}
int[][] matrix = new int[n][n];
for (int k = 0; k < matrix.length; k++) {
for (int l = 0; l < matrix[0].length; l++) {
matrix[k][l] = square[k + 1][l + 1];
}
}
return matrix;
}
public static void main(String[] args) {
int[][] magic = Matrix.magicOdd(5);
for (int k = 0; k < magic.length; k++) {
for (int l = 0; l < magic[0].length; l++) {
System.out.print(magic[k][l] + " ");
}
System.out.println();
}
}
}
(26)4N魔方阵
说明:
与 奇数魔术方阵 相同,在于求各行、各列与各对角线的和相等,而这次方阵的维度是4的倍数。
解法:
先来看看4X4方阵的解法:
简单的说,就是一个从左上由1依序开始填,但遇对角线不填,另一个由左上由16开始填,但只填在对角线,再将两个合起来就是解答了;如果N大于2,则以 4X4为单位画对角线:
至于对角线的位置该如何判断,有两个公式,有兴趣的可以画图印证看看,如下所示:
左上至右下:j % 4 == i % 4
右上至左下:(j % 4 + i % 4) == 1
实现:
public class Matrix2 {
public static int[][] magicFourN(int n) {
int[][] square = new int[n + 1][n + 1];
for (int j = 1; j <= n; j++) {
for (int i = 1; i <= n; i++) {
if (j % 4 == i % 4 || (j % 4 + i % 4) == 1) square[i][j] = (n + 1 - i) * n - j + 1;
else square[i][j] = (i - 1) * n + j;
}
}
int[][] matrix = new int[n][n];
for (int k = 0; k < matrix.length; k++) {
for (int l = 0; l < matrix[0].length; l++) {
matrix[k][l] = square[k + 1][l + 1];
}
}
return matrix;
}
public static void main(String[] args) {
int[][] magic = Matrix2.magicFourN(8);
for (int k = 0; k < magic.length; k++) {
for (int l = 0; l < magic[0].length; l++) {
System.out.print(magic[k][l] + " ");
}
System.out.println();
}
}
}
(27)2(2n+1)魔方阵
说明:
方阵的维度整体来看是偶数,但是其实是一个奇数乘以一个偶数,例如6X6,其中6=2X3,我们也称这种方阵与单偶数方阵。
解法:
如果您会解奇数魔术方阵,要解这种方阵也就不难理解,首先我们令n=2(2m+1),并将整个方阵看作是数个奇数方阵的组合,如下所示:
首先依序将A、B、C、D四个位置,依奇数方阵的规则填入数字,填完之后,方阵中各行的和就相同了,但列与对角线则否,此时必须在A-D与C- B之间,作一些对应的调换,规则如下:
将A中每一列(中间列除外)的头m个元素,与D中对应位置的元素调换。
将A的中央列、中央那一格向左取m格,并与D中对应位置对调
将C中每一列的倒数m-1个元素,与B中对应的元素对调
举个实例来说,如何填6X6方阵,我们首先将之分解为奇数方阵,并填入数字,如下所示:
接下来进行互换的动作,互换的元素以不同颜色标示,如下:
实现:
public class Matrix3 {
public static int[][] magic22mp1(int n) {
int[][] square = new int[n][n];
magic_o(square, n / 2);
exchange(square, n);
return square;
}
private static void magic_o(int[][] square, int n) {
int row = 0;
int column = n / 2;
for (int count = 1; count <= n * n; count++) {
square[row][column] = count;
// 填A
square[row + n][column + n] = count + n * n;
// 填B
square[row][column + n] = count + 2 * n * n;
// 填C
square[row + n][column] = count + 3 * n * n;
// 填D
if (count % n == 0) row++;
else {
row = (row == 0) ? n - 1 : row - 1;
column = (column == n - 1) ? 0 : column + 1;
}
}
}
private static void exchange(int[][] x, int n) {
int i, j;
int m = n / 4;
int m1 = m - 1;
for (i = 0; i < n / 2; i++) {
if (i != m) {
for (j = 0; j < m; j++)
// 处理规则 1
swap(x, i, j, n / 2 + i, j);
for (j = 0; j < m1; j++)
// 处理规则 2
swap(x, i, n - 1 - j, n / 2 + i, n - 1 - j);
} else {
// 处理规则 3
for (j = 1; j <= m; j++) swap(x, m, j, n / 2 + m, j);
for (j = 0; j < m1; j++) swap(x, m, n - 1 - j, n / 2 + m, n - 1 - j);
}
}
}
private static void swap(int[][] number, int i, int j, int k, int l) {
int t;
t = number[i][j];
number[i][j] = number[k][l];
number[k][l] = t;
}
public static void main(String[] args) {
int[][] magic = Matrix3.magic22mp1(6);
for (int k = 0; k < magic.length; k++) {
for (int l = 0; l < magic[0].length; l++) {
System.out.print(magic[k][l] + " ");
}
System.out.println();
}
}
}
————————————————
何为二分查找
1,前提:有已排序数组 A (假设已经做好)
2.定义左边界 L 、右边界 R ,确定搜索范围,循环执行二分查找(3、4两步)
3.获取中间索引 M = Floor (( L + R )/2)
4.中间索引的值 A [ M ] 与待搜索的值 T 进行比较
① A [ M ]= T 表示找到,返回中间索引
② A [ M ]> T ,中间值右侧的其它元素都大于 T ,无需比较,中间索引左边去找, M - 1设置为右边界,重新查找
③ A [ M ]< T ,中间值左侧的其它元素都小于 T ,无需比较,中间索引右边去找, M + 1设置为左边界,重新查找
/***
* 2分查找
*/
public class HalfFind {
public static void main(String[] args) {
int[] arr = {1,11,24,33,45,48,56,68,69,73,77,83,85,90,99,107};
int target = 99;
System.out.println(halfFind(arr,target));
}
private static String halfFind(int[] arr, int target) {
// l:左边界 r:右边界 m:中间索引
int l = 0,r = arr.length-1,m;
// 记录查找次数
int num = 0;
// 如果左边界大于右边界说明没有找到数据退出循环
while (l <= r) {
num++;
// m = (l + r) / 2;
//使用右移1位 可以解决int最大数值数据溢出问题 不考虑大数据量可以直接使用 m = (l + r) / 2;
m = (l + r) >>> 1;
if (arr[m] == target) {
return "查找"+num+"次,找到该元素的索引是:"+m;
} else if (arr[m] > target) {
//说明中间索引右侧元素都大于target 右侧不用比较 把右边界改为 m-1
r = m - 1;
} else {
//说明中间索引左侧元素都小于target 左侧不用比较 把左边界改为 m+1
l = m + 1;
}
}
return "查找"+num+"次,没有找到该元素!";
}
}




