第1章 信号与系统
Ø 信号的数学定义:连续信号和离散信号
Ø 自变量的变换:时移、反转和尺度变换
Ø 指数信号和正弦信号
Ø 单位冲激和单位阶跃函数
Ø 连续时间和离散时间系统
Ø 基本系统性质
-
信号的定义
- 数学定义:一个或多个变量的函数
-
信号的能量与功率
-
数学定义
![]()
-
Ø无穷区间内的功率和能量
![]()
![]()
![]()
能量有限信号的平均功率必为0;非0功率信号的能量无限
-
-
自变量的变换
- 平移(时移)变换
- 时间反转(镜像)变换
- 尺度变换
-
周期信号
Ø周期连续时间信号x(t)是指x(t)= x(t+T)
• 信号x(t)时移T值不发生改变
• T称为周期
• 最小的正值周期称为基波周期
• 周期的倒数称为频率
Ø周期离散时间信号x[n]是指x[n]=x[n+N]
• N称为周期,其他定义类似
• N必须为非0整数
-
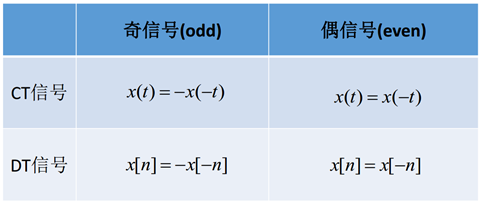
奇信号和偶信号
![]()
Ø奇信号偶信号分解:任何一个信号必然能分解为一个偶信号和一个奇信号之和
![]()
Ø 信号的数学定义:连续信号和离散信号
Ø 自变量的变换:时移、反转和尺度变换
Ø 指数信号和正弦信号
Ø 单位冲激和单位阶跃函数
Ø 连续时间和离散时间系统
Ø 基本系统性质
-
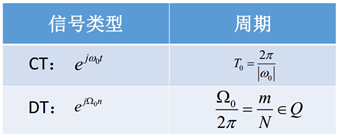
连续时间正弦信号
![]()
-
连续时间复指数信号
![]()
-
连续时间周期复指数信号
![]()
-
连续时间一般复指数信号
![]()
-
离散时间正弦信号
![]()
-
离散时间复指数信号(序列)
![]()
-
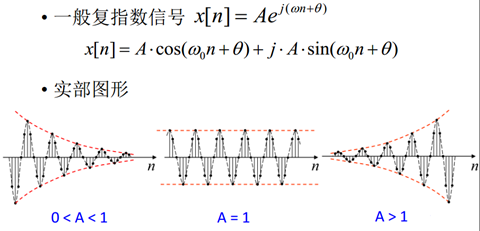
离散时间一般复指数信号
![]()
-
离散时间复指数序列的周期性
![]()
![]()
-
补充知识:谐波
![]()
Ø 信号的数学定义:连续信号和离散信号
Ø 自变量的变换:时移、反转和尺度变换
Ø 指数信号和正弦信号
Ø 单位冲激和单位阶跃函数
Ø 连续时间和离散时间系统
Ø 基本系统性质
-
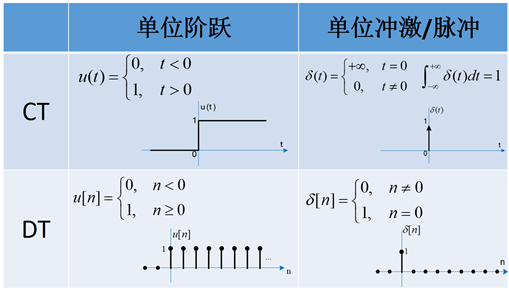
离散时间单位脉冲信号( unit impulse signal)
![]()
-
离散时间单位阶跃信号(unit step signal)
![]()
-
离散时间单位脉冲信号和离散时间单位阶跃信号的关系
- 单位脉冲δ[n]是单位阶跃信号u[n]的一次差分:δ[n]=u[n]-u[n-1]
![]()
-
连续时间单位阶跃函数
![]()
• 注意u(t)在0点未定义,不连续
• 物理意义:状态间的理想化的瞬间跳跃
• 应用:( 1)可以方便地表示某些信号( 2)可以表示信号的作用区间
![]()
-
连续时间单位冲激函数
![]()
•也称为狄拉克函数( Dirac delta function)
•仅在0点有值,且为无穷大,其他点为0
•无穷区间内积分为1
-
单位冲激和单位阶跃的关系
![]()
![]()
-
单位冲激函数的应用及性质
( 1)不连续函数求导
• 引入冲激函数之后,间断点的导数也可表示
![]()
(2)冲激函数的尺度变换
![]()
Ø 信号的数学定义:连续信号和离散信号
Ø 自变量的变换:时移、反转和尺度变换
Ø 指数信号和正弦信号
Ø 单位冲激和单位阶跃函数
Ø 连续时间和离散时间系统
Ø 基本系统性质
-
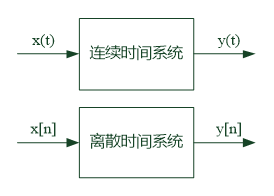
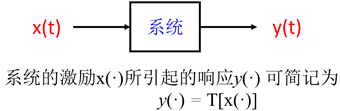
系统
- 定义:若干相互作用、相互联系的事物按一定规律组成具有特定功能的整体
![]()
-
系统互联
-
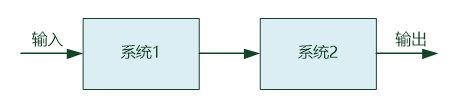
级联
![]()
-
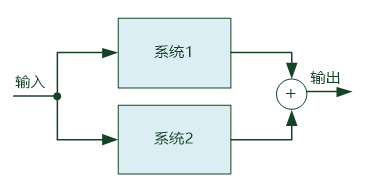
并联
![]()
-
混合连接
![]()
-
反馈连接
![]()
-
-
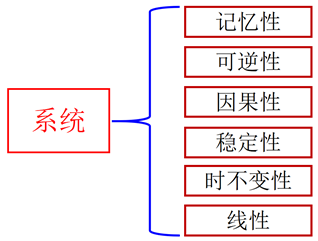
系统的基本性质
![]()
-
记忆性
• 记忆系统:若系统在任一时刻的响应不仅与该时刻的激励有关,而且与它过去的状况有关
• 无记忆系统:若对自变量的任意值,输出仅决定于该时刻的输入
-
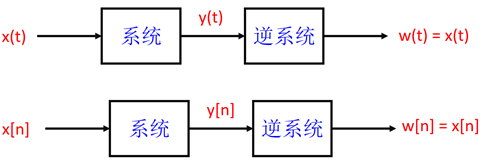
可逆性
• 如果一个系统中不同的输入下,导致不同的输出,就称为系统是可逆的(单射)
• 如果系统可逆,就存在一个逆系统,使得两个系统级联后,形成恒等系统
![]()
-
因果性
• 如果一个系统在任何时刻的输出只决定于现在和过去的输入,该系统就称为因果系统。
• 由系统的输出无法预测未来输入,也称为不可预测的系统
• 现实世界的大部分系统是因果的,非因果系统通常无法实现
• 无记忆系统为因果系统
-
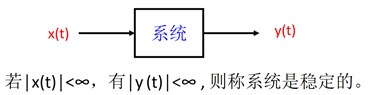
稳定性
• 任意有界输入,对应的输出有界
![]()
-
时不变性
• 系统行为不随时间发生改变
![]()
直观判断方法:若x (·)前出现变系数,或有反转、展缩变换,则系统为时变系统。
-
线性
• 满足线性性质的系统称为线性系统
• 线性性质: 齐次性和可加性
![]()
•齐次性:若系统的激励f (·)增大a倍时,其响应y(·)也增大a倍,即:
![]()
•可加性:若系统对于激励x1(·)与x2(·)之和的响应等于各个激励所引起的响应之和,即:
![]()
-
第一章到此结束
Ø 信号的数学定义:连续信号和离散信号
Ø 自变量的变换:时移、反转和尺度变换
Ø 指数信号和正弦信号
Ø 单位冲激和单位阶跃函数
Ø 连续时间和离散时间系统
Ø 基本系统性质




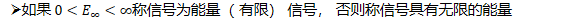






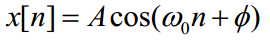

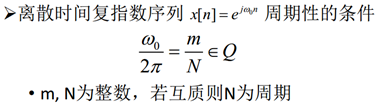



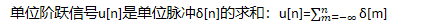
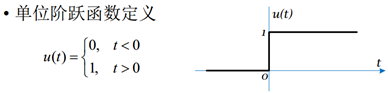




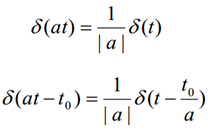


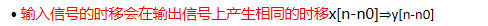
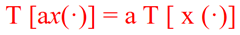
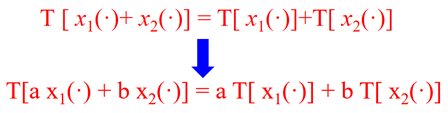

 浙公网安备 33010602011771号
浙公网安备 33010602011771号