蓝书乱刷

P2862 [USACO06JAN] Corral the Cows G

题意简述

给定一个网格 \(L \times L\)，上面有 \(N\) 个叶子，求最小的正方形边长，使得这个正方形能够覆盖至少 \(C\) 个叶子

题解

很显然是一道二分 + 前缀和的题目，一眼 \(O(L^2 + N \log L)\)

但是题目里 \(L\) 非常大，带个平方过不去，所以考虑对叶子坐标进行离散化，离散化之后的复杂度能降到 \(O(N^2 + N \log L)\)

问题是，本题里我们需要考虑原数据的大小啊，不然没法求边长

所以用离散化做的难点在于，代码中对原始数据和离散化数据的转换非常多

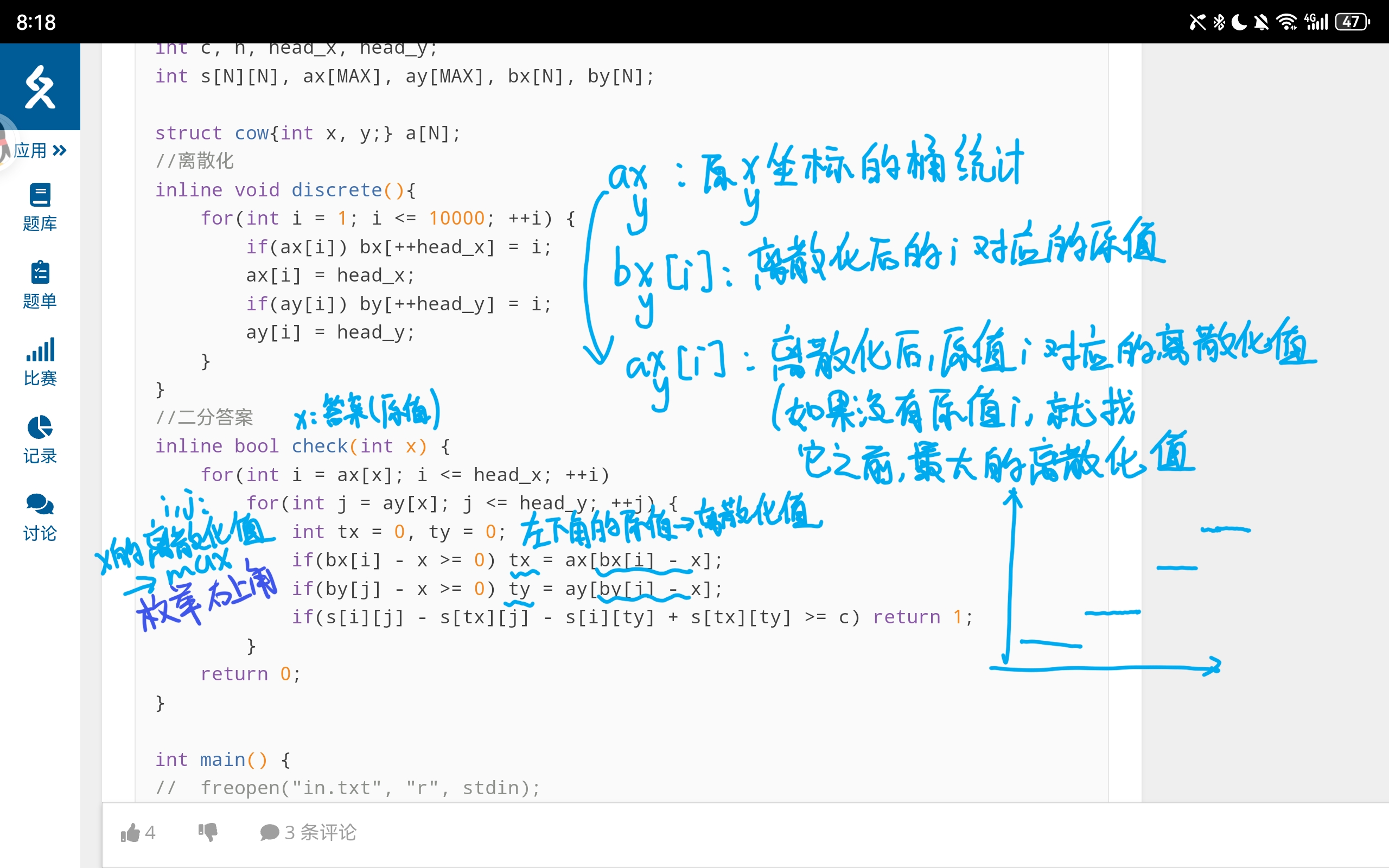
只有90分，我也调不出来了

const int MAXL = 1e5 + 10;
const int MAXN = 5000 + 10;

struct Node {
    int x, y;
    bool operator < (const Node &that) const {
        return x == that.x ? y < that.y : x < that.x;
    }
} node[MAXN]; 

int n, c;
int index[MAXL], ori[MAXL], cnt; bool exi[MAXL];
int sum[MAXN][MAXN];

void lisan() {
    for (int i_o = 1; i_o <= MAXL - 10; ++i_o) {
        if (exi[i_o]) {
            ori[++cnt] = i_o;
        } index[i_o] = cnt;
    }
}

bool check(int len) {
    // DEBUG(index[len]);
    for (int tx_n = index[len]; tx_n <= cnt; ++tx_n) {
        for (int ty_n = index[len]; ty_n <= cnt; ++ty_n) {
            // (rx - len, ry - len) 就已经是左下角的前一个了
            // 无需再次减一
            if (ori[tx_n] - len < 0 || ori[ty_n] - len < 0) continue;
            int lx_n = index[ori[tx_n] - len], ly_n = index[ori[ty_n] - len];
            int ss = sum[tx_n][ty_n] - sum[tx_n][ly_n] - sum[lx_n][ty_n] + sum[lx_n][ly_n];
            if (ss >= c) return true;
        } 
    } return false;
}

int main() {
    c = read(); n = read();
    for (int i = 1; i <= n; ++i) {
        node[i].x = read(); node[i].y = read();
        exi[node[i].x] = exi[node[i].y] = true;
    } lisan();
    for (int i = 1; i <= n; ++i) {
        node[i].x = index[node[i].x];
        node[i].y = index[node[i].y];
        ++sum[node[i].x][node[i].y];
        // DEBUG(node[i].x);
    }
    for (int i = 1; i <= cnt; ++i) {
        for (int j = 1; j <= cnt; ++j) {
            sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
        }
    }
    int l = 1, r = ori[cnt], ans = r;
    while (l <= r) {
        int mid = (l + r) >> 1;
        if (check(mid)) {
            ans = mid, r = mid - 1;
        } else l = mid + 1;
    } printf("%d\n", ans);
    return 0;
}

POJ 1050 To The Max

题意简述

给定一个 \(N\times N\) 的矩阵，求一个正方形使得数字和最大

题解

一行很好做，你既可以说是贪心也可以说是 DP：设 dp[i] 表示以 i 结尾的最大子串和，显然 dp[i] = max(dp[i - 1] + aa[i], aa[i])

但是这时候是个矩阵，怎么办？

我们考虑降维打击！

将多个连续的行压缩成一行，对应元素的值相加，然后对这一行做 DP，就相当于是对原矩阵中多个连续的行做 DP 了！

一共有 \(\frac{1}{2}N(N-1)\) 个这样的连续行组合，总时间复杂度 \(O(N^3)\)

const int MAXN = 100 + 10;

int n, mat[MAXN][MAXN];
int calc[MAXN];
int ans;

void DP() {
    static int dp[MAXN];
    for (int i = 1; i <= n; ++i) {
        dp[i] = std::max(dp[i - 1] + calc[i], calc[i]);
        ans = std::max(ans, dp[i]);
    } 
}

int main() {
    n = read();
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) mat[i][j] = read();
    }
    for (int l = 1; l <= n; ++l) {
        for (int i = 1; i <= n; ++i) calc[i] = mat[l][i];
        DP();
        for (int t = l + 1; t <= n; ++t) {
            for (int i = 1; i <= n; ++i) calc[i] += mat[t][i];
            DP();
        }
    } printf("%d\n", ans);
}