洛谷P1821《[USACO07FEB]银牛派对Silver Cow Party》
原创建时间:2018-07-20 12:57:21
巧妙地把单终点最短路径问题转化为单源最短路径问题
题目描述
寒假到了,N头牛都要去参加一场在编号为X(1≤X≤N)的牛的农场举行的派对(1≤N≤1000),农场之间有M(1≤M≤100000)条有向路,每条路长Ti(1≤Ti≤100)。
每头牛参加完派对后都必须回家,无论是去参加派对还是回家,每头牛都会选择最短路径,求这N头牛的最短路径(一个来回)中最长的一条路径长度。
Input/Output 格式 & 样例
输入格式:
第一行三个整数N,M, X;
第二行到第M+1行:每行有三个整数Ai,Bi, Ti ,表示有一条从Ai农场到Bi农场的道路,长度为Ti。
输出格式:
一个整数,表示最长的最短路得长度。
输入样例#1:
4 8 2
1 2 4
1 3 2
1 4 7
2 1 1
2 3 5
3 1 2
3 4 4
4 2 3
输出样例#1:
10
题目说明
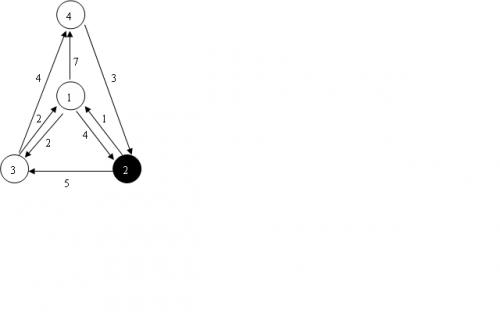
图片来自洛谷
解题思路
单源最短路我们都会做,一遍SPFA或Dijkstra就行了。
单终点最短路呢?
对于这道题,奶牛们从派对分别回家就是一个单源最短路问题,而奶牛们从家到派对就是一个单终点最短路问题。
如何把单终点最短路转化为单源最短路问题?
注意:题目中建的是有向边
实在是想不出来的我翻了一波题解,发现他们都在输入的时候另建了一个图,反向存边,就完美地把一个单终点最短路转化为单源最短路
因为单源和单终点的区别仅仅是方向改变,很显然这么做是对的
最后的答案是什么?
正向建图的距离+反向建图的距离的最大值
代码实现
我们在数组后加上「Reversed」,表示它存的是反向的图
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <queue>
using namespace std;
const int MAXN = 1000 + 10;
const int MAXM = 100000 + 10;
struct Edge {
int prev;
int next;
int weight;
} edge[MAXM], edgeReversed[MAXM];
int n, m, x, cnt, maxWeight = -1;
int dis[MAXN], head[MAXN], disReversed[MAXN], headReversed[MAXN];
bool inQueue[MAXN], inQueueReversed[MAXN];
inline int getint() {
int s = 0, x = 1;
char ch = getchar();
while (!isdigit(ch)) {
(ch == '-') && (x = -1);
ch = getchar();
}
while (isdigit(ch)) {
s = s * 10 + ch - '0';
ch = getchar();
}
return s * x;
}
inline void addEdgeReversed(int prev, int next, int weight) {
edgeReversed[cnt].prev = prev;
edgeReversed[cnt].weight = weight;
edgeReversed[cnt].next = headReversed[next];
headReversed[next] = cnt;
}
inline void addEdge(int prev, int next, int weight) {
edge[++cnt].prev = prev;
edge[cnt].weight = weight;
edge[cnt].next = head[next];
head[next] = cnt;
addEdgeReversed(next, prev, weight);
}
inline void Dijkstra(int s, int n) {
memset(inQueue, 0, sizeof(inQueue));
for (int i = 0; i <= n; ++i) dis[i] = 2147483647;
std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int> >, std::greater<std::pair<int, int> > > q;
inQueue[s] = true;
q.push(make_pair(s, 0));
dis[s] = 0;
while (!q.empty()) {
int prev = q.top().first;
int weight = q.top().second;
q.pop();
inQueue[prev] = false;
for (int e = head[prev]; e; e = edge[e].next) {
if (dis[edge[e].prev] > edge[e].weight + weight) {
dis[edge[e].prev] = edge[e].weight + weight;
q.push(make_pair(edge[e].prev, dis[edge[e].prev]));
}
}
}
}
inline void DijkstraReversed(int s, int n) {
memset(inQueueReversed, 0, sizeof(inQueueReversed));
for (int i = 0; i <= n; ++i) disReversed[i] = 2147483647;
std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int> >, std::greater<std::pair<int, int> > > q;
inQueueReversed[s] = true;
q.push(make_pair(s, 0));
while (!q.empty()) {
int prev = q.top().first;
int weight = q.top().second;
q.pop();
inQueueReversed[prev] = false;
for (int e = headReversed[prev]; e; e = edgeReversed[e].next) {
if (disReversed[edgeReversed[e].prev] > edgeReversed[e].weight + weight) {
disReversed[edgeReversed[e].prev] = edgeReversed[e].weight + weight;
q.push(make_pair(edgeReversed[e].prev, disReversed[edgeReversed[e].prev]));
}
}
}
}
int main(int argc, char *const argv[]) {
n = getint(), m = getint(), x = getint();
int tm = m;
while (tm --> 0) {
int prev = getint(), next = getint(), weight = getint();
addEdge(prev, next, weight);
}
int tn = n;
Dijkstra(x, n);
DijkstraReversed(x, n);
for (int i = 1; i <= n; ++i) {
maxWeight = std::max(maxWeight, dis[i] + disReversed[i]);
}
printf("%d\n", maxWeight);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号