【CTF入门】BUUCTF Crypto刷题（持续更新）

一眼就解密

题目介绍如图：

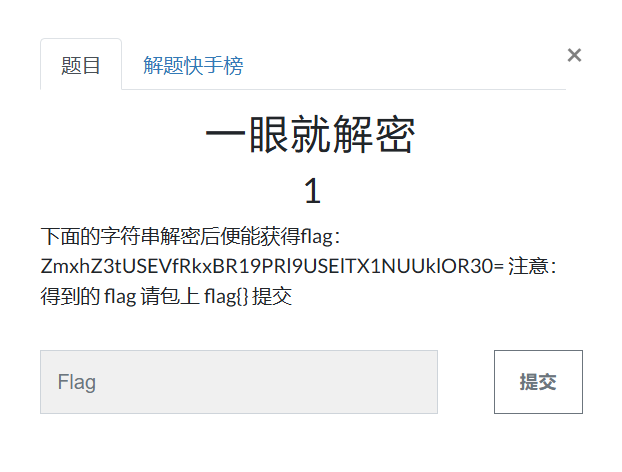
我们可以发现加密的字符串由base64编码，因此base64解码后即可解密。什么是base64编码，又应该如何解码呢？

base64编码介绍

原理：https://www.bilibili.com/video/BV1hk4y1S7PJ?vd_source=69c558b0c7be97607c79afbd75bd1f7c

密文特征：

乱码尾部通常有一两个等号。

回到题目，base64解码并不是很难的事，在网上搜索base64解码都能搜索出很多在线工具可以进行解码：

个人常用解码工具网址为：CyberChef，它还有离线版本，是非常强大的集合解密工具。

使用工具base64解码后即可获得flag

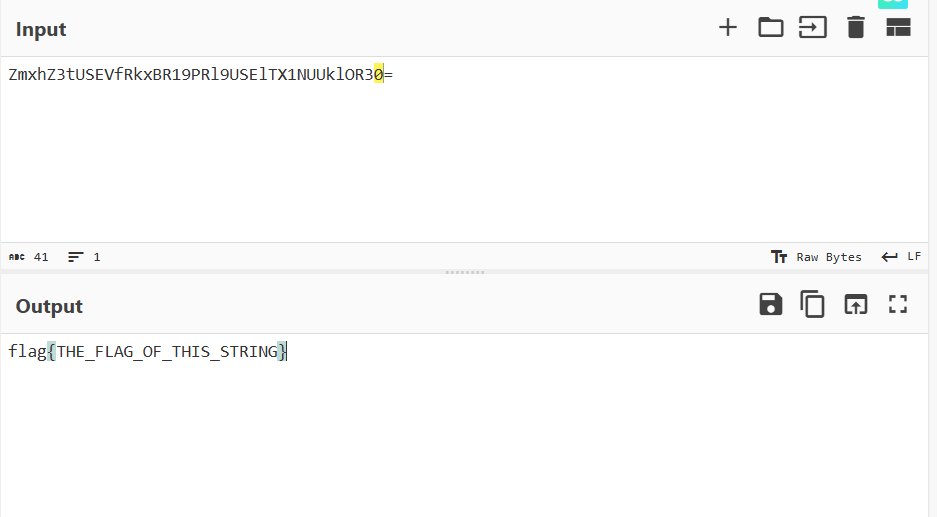
考点：base64解码

MD5

下载文件，打开发现加密字符串：

根据题目名我们可以知道字符串经历了MD5算法加密，那么我们应该怎么解密呢？

HASH算法介绍

MD5系列算法是HASH算法的一种，在此我们介绍下什么是HASH算法。

原理：https://www.bilibili.com/video/BV1SZ4y1z7wT?vd_source=69c558b0c7be97607c79afbd75bd1f7c

密文特征：

都是固定长度，常见经历过MD5算法加密的密文为32位字符串。

回到题目，通过学习我们知道HASH算法是不可逆向运算的，但如果明文是非常简单的字符串我们还是可以基于暴力破解和彩虹表来进行解密的。（MD5解密本质上是加速了杂凑冲撞，即找到产生相同MD5串的原文的方法，而不是真正的解密）

在此推荐一些MD5解密在线网站：md5在线解密破解,md5解密加密 (cmd5.com)

Decrypt MD5, SHA1, MySQL, NTLM, SHA256, MD5 Email, SHA256 Email, SHA512, Wordpress, Bcrypt hashes for free online

CrackStation - Online Password Hash Cracking - MD5, SHA1, Linux, Rainbow Tables, etc.

还有一些破解MD5的工具：hashcat、John the Ripper在此不过多介绍

我们在在线网站上进行解密，得到了flag内容：

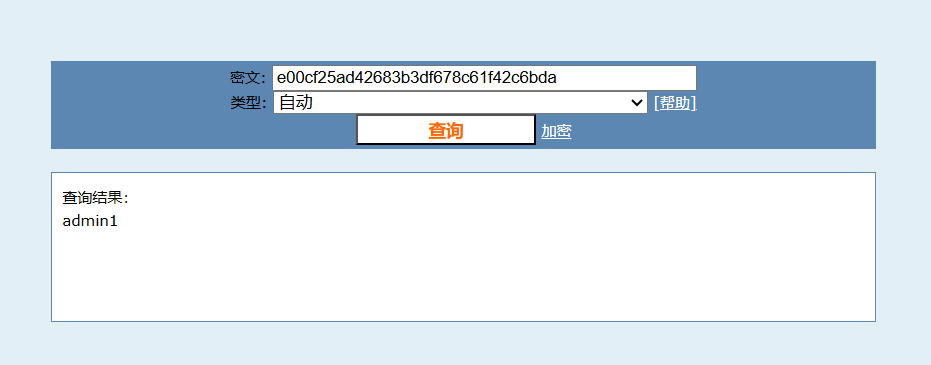
按照题目说明，包上flag{}提交

考点：MD5系列算法解密

Url编码

下载文件，打开发现加密字符串：

我们可以发现加密的字符串由url编码，因此url解码后即可解密。什么是url编码？

Url编码介绍

URL 编码是将 URL 中不可打印的字符或具有特殊含义的字符转换为 Web 浏览器和服务器普遍接受的字符的过程。例如！ -> %21；# -> %23等。

密文特征：

都是由 "%"和十六进制数字组成。

回到题目，使用解码工具即可解密：

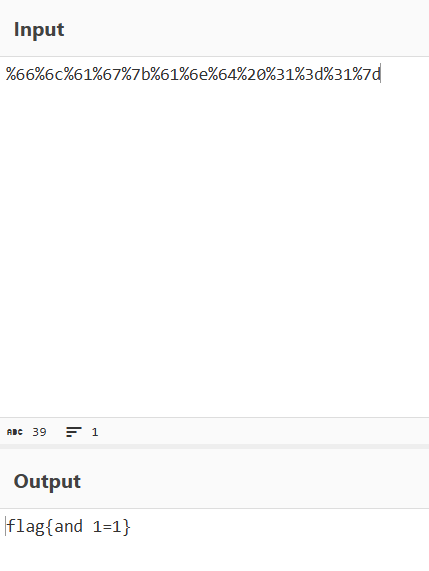
考点：理解url编码

看我回旋踢

下载文件，打开发现加密字符串：

根据密文特征与题目提示（回旋踢），我们可以确定加密方式为ROT13加密（回转13位）

ROT13加密介绍

是一种简易的替换式密码算法，也是过去在古罗马开发的凯撒密码的一种变体。

原理：

密文特征：

纯乱码，但flag的格式不会改变。个人认为得靠提示与运气。

回到题目，使用解码工具即可解密：

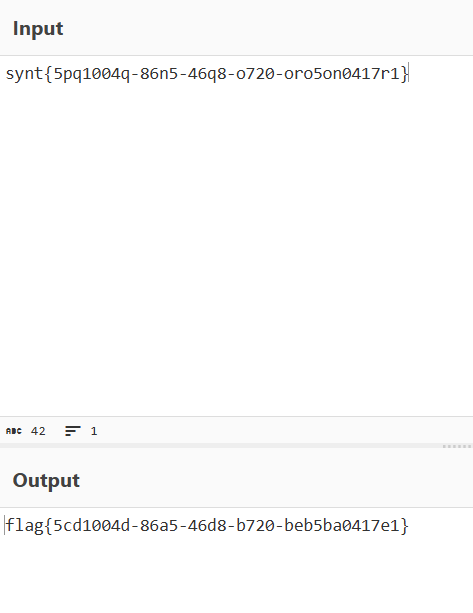
考点：理解ROT13加密

摩丝

下载文件，打开发现加密字符串：

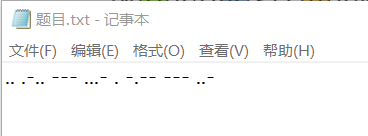
鉴定为大名鼎鼎的摩斯电码，可以直接上工具

摩斯电码介绍

原理：摩尔斯电码_百度百科 (baidu.com)

密文特征：

只有两种格式的字符串。

回到题目，使用解码工具即可解密：

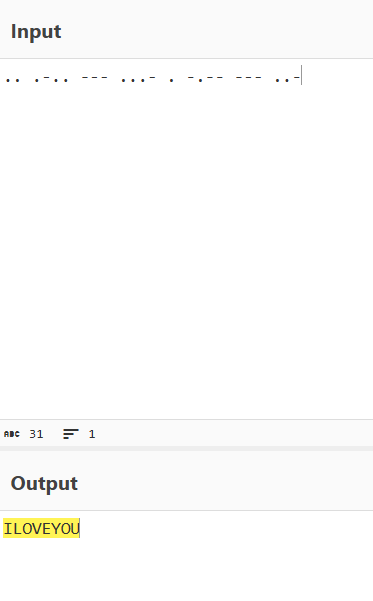
考点：知道摩斯电码加密

password

下载文件，打开发现这些：

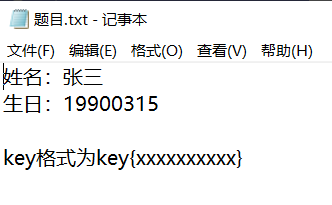
一看让人摸不着头脑，让我们发散思维，根据题目名（password）这是让我们猜测张三的密码。这涉及到社会工程学攻击。

社会工程学

原理：https://www.bilibili.com/video/BV15V411u7Za?vd_source=69c558b0c7be97607c79afbd75bd1f7c

根据题目内容，我们已经得到了张三的生日信息以及密码为十位数。这是一道CTF题目，根据已有信息我们可以进行排列组合猜测密码：zs19900315、Zs19900315、zS19900315、ZS19900315、19900315zs……

包上flag{}提交，猜测正确

考点：发散思维想到社工打击

变异凯撒

下载文件，打开发现这些：

根据题目我们可以知道这是与凯撒密码相关的，也就是与位移密码相关。

密文中含有特殊字符，因此以ascii表对密文与明文进行对照，根据格式我们可以知道”flag“经过加密后的密文为“afZ_”

CS50. Си. ASCII

f——102，a——97 相差5
l——108，f——102 相差6
a——97，Z——90 相差7
g——103，_——95 相差8

按照这个规律，我们可以依次计算下去，或者是自己编写python脚本来进行解密：

ciphertext = 'afZ_r9VYfScOeO_UL^RWUc'
j = 5
for i in ciphertext:
    print(chr(ord(i) + j), end='') #凯撒密码从5开始递增
    j += 1

ord()：返回一个字符的ASCII值

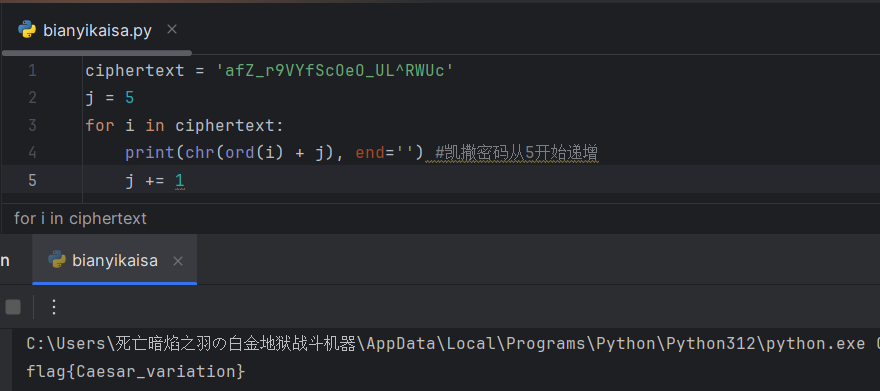
最终运算出flag

考点：寻找出移位密码的规律

Quoted-printable

下载文件，打开发现加密字符串：

鉴定为Quoted-printable编码，可以直接上工具

Quoted-printable编码介绍

原理：

Q：试将数据 01001100 10011101 00111001进行quoted-printable编码，并得出最后传送的ASCII编码。
A：
在这里插入图片描述

（来源：MIME之quoted-printable编码与base64编码（例题+图解）-CSDN博客）

密文特征：

以一个“=”和两位十六进制数字堆积组成字符串。

回到题目，由cyberchef工具可以得到：

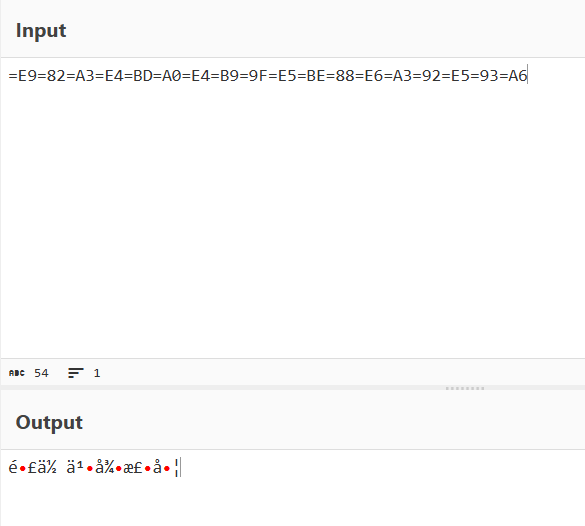
怎么乱码了？别急，cyberchef的输出编码出了问题，这道题目的flag很有可能不是英文字符

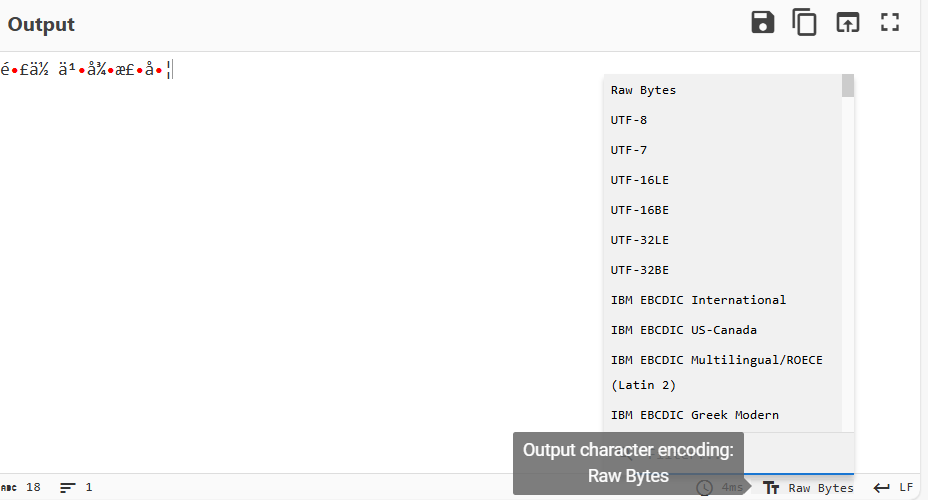
我们在output底下那一栏更改输出字符编码方式，改为utf-8即可

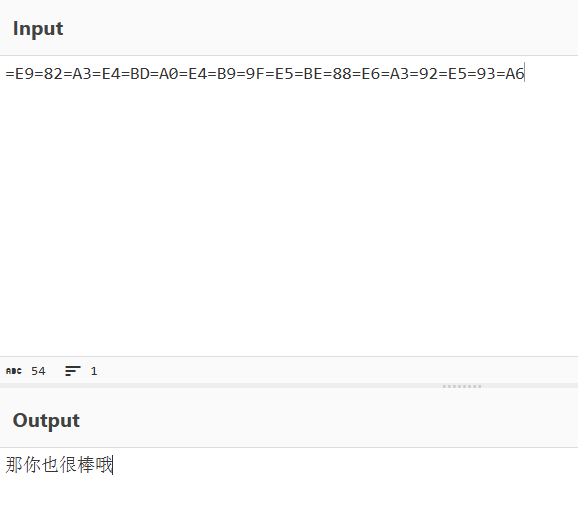
包上flag{}，提交成功

补充：UTF-8编码

原理：https://www.bilibili.com/video/BV1kD4y1z7ft?vd_source=69c558b0c7be97607c79afbd75bd1f7c

篱笆墙的影子

下载文件，打开发现加密字符串：

根据题目名字，这很有可能是栅栏（篱笆：fence）密码

栅栏密码介绍

原理：https://www.bilibili.com/video/BV1TE41177qP?vd_source=69c558b0c7be97607c79afbd75bd1f7c

密码特征：

flag{}格式的“{}”不在它应该在的位置。

我们进行分析，发现flag{的位置：

可以推断出栅栏栏数为2，如果实在不想推直接把所有栏数都爆破一遍也行

用栅栏密码加密后发现了flag：

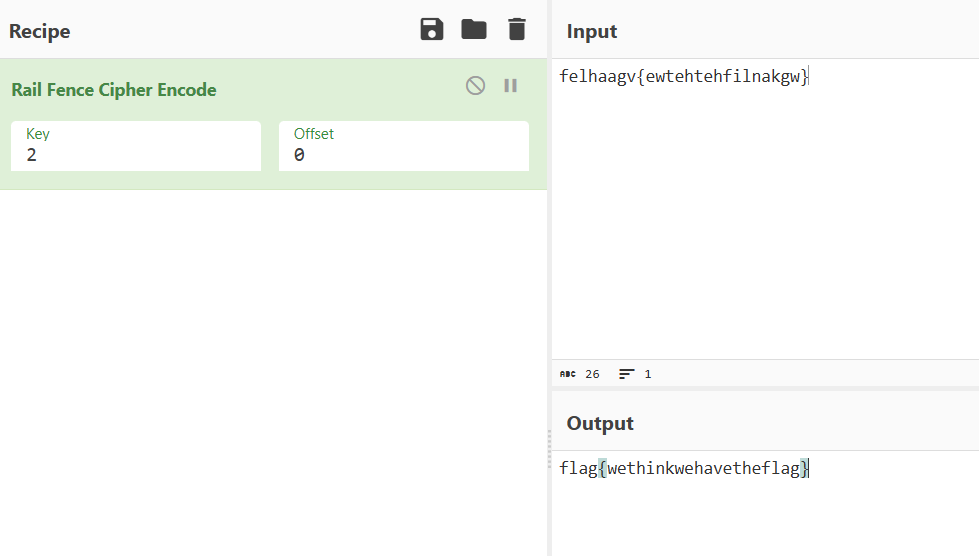
Rabbit

下载文件，打开发现加密字符串：

根据题目名，我们能知道字符串进行了rabbit加密。

Rabbit加密介绍

Rabbit 是一种高速流密码，于 2003 年在 FSE 研讨会上首次提出。 Rabbit 使用一个 128 位密钥和一个 64 位初始化向量。该加密算法的核心组件是一个位流生成器，该流生成器每次迭代都会加密 128 个消息位。（来源：【BUUCTF】Crypto题解_buuctf crypto答案-CSDN博客）

在这里插入图片描述

用解密工具进行解密：

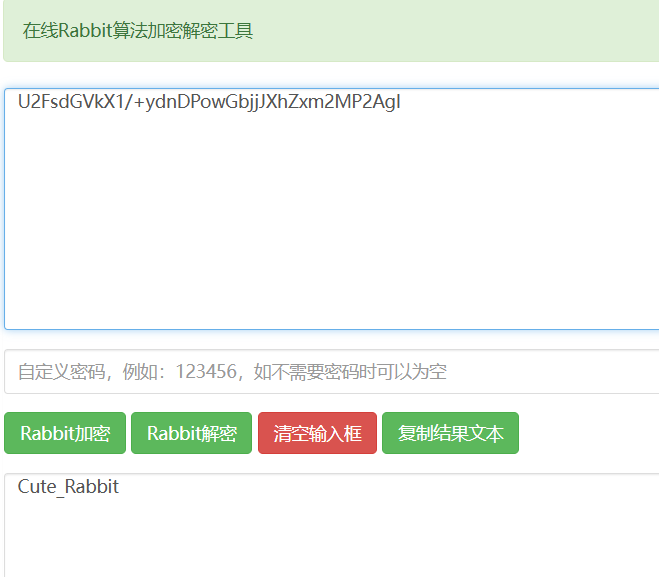
cyberchef可能只能使用需要秘钥的rabbit加密，所以在此使用了其他在线网站解出了flag

RSA

下载文件，打开发现这些：

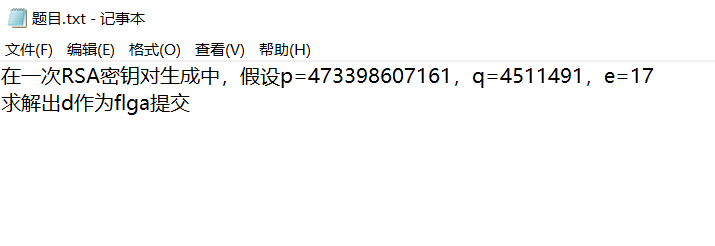
这更类似于一道数学题，在此之前我们先学习一下RSA的算法步骤

RSA加密介绍

原理：https://www.bilibili.com/video/BV1XP4y1A7Ui?vd_source=69c558b0c7be97607c79afbd75bd1f7c

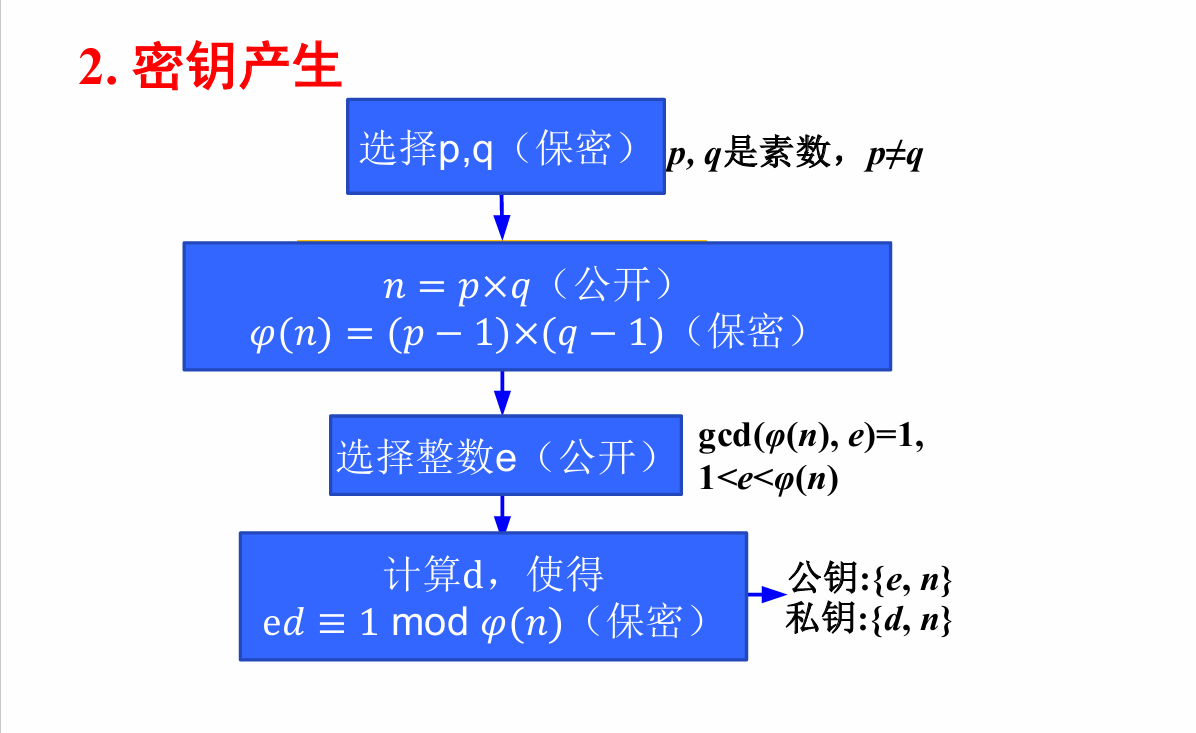
知道了RSA的算法后我们便能够计算d的值了，直接编写脚本：

p = 473398607161
q = 4511491
e = 17
n = p*q
phi = (p-1)*(q-1)
d = pow(e,-1,phi)
print(d)

pow()：返回e的-1次方，并对结果与phi进行模运算

运行脚本，我们可以得到d的值：125631357777427553

考点：理解RSA加密原理并运用p、q、e计算出d

丢失的MD5

下载文件，打开发现这些：

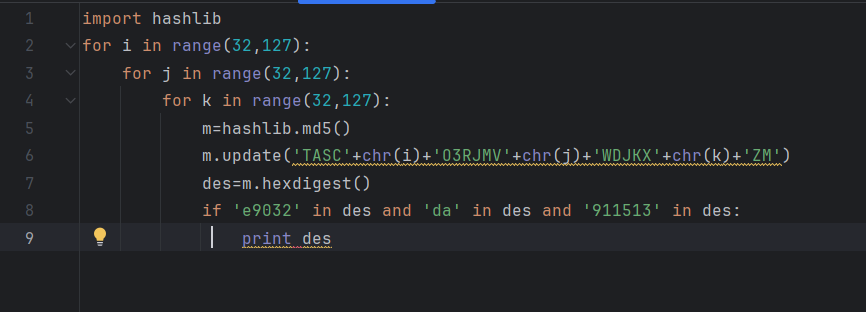
我们对脚本进行分析：

import hashlib	#导入hashlib库：这个库提供了多种哈希算法，如MD5、SHA-1等，用于生成数据的哈希值。
for i in range(32,127):
    for j in range(32,127):
        for k in range(32,127):
            m=hashlib.md5()	# 创建一个新的MD5对象
            m.update('TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM')	# 嵌套循环生成字符串，并计算字符串的MD5哈希值
            des=m.hexdigest()	#获取哈希值的十六进制表示
            if 'e9032' in des and 'da' in des and '911513' in des:	#检查哈希值是否包含指定的字符串
                print des	#输出哈希值

脚本在计算明文'TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM'的MD5哈希值，并只输出含有'e9032'、'da'和'911513'三个字符串的密文，按照一般思路我们应该寻找相应的明文。

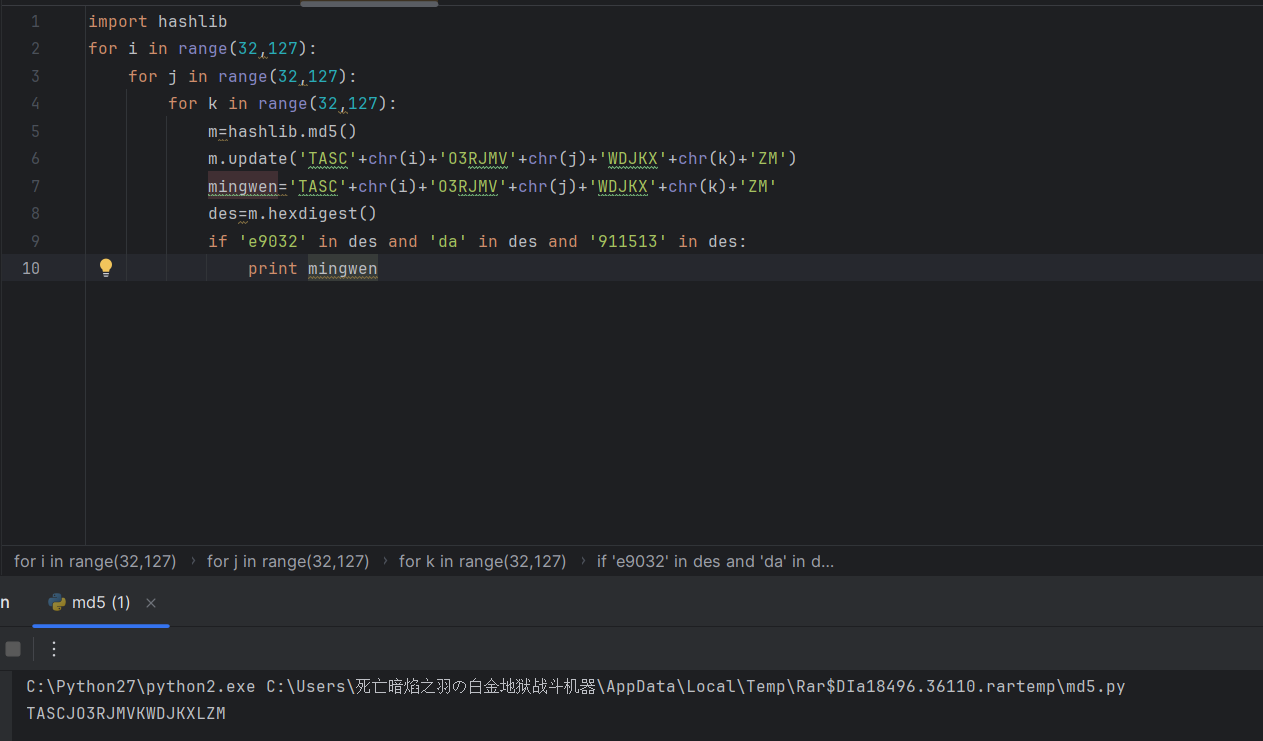
很简单，我们修改一下程序就能输出相关明文：

import hashlib	#导入hashlib库：这个库提供了多种哈希算法，如MD5、SHA-1等，用于生成数据的哈希值。
for i in range(32,127):
    for j in range(32,127):
        for k in range(32,127):
            m=hashlib.md5()	# 创建一个新的MD5对象
            m.update('TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM')	# 嵌套循环生成字符串，并计算字符串的MD5哈希值
            mingwen='TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM'	#记录生成的字符串
            des=m.hexdigest()	#获取哈希值的十六进制表示
            if 'e9032' in des and 'da' in des and '911513' in des:	#检查哈希值是否包含指定的字符串
                print mingwen	#输出符合条件的明文

运行脚本就有了：

但是提交发现是错误的！！！为什么！！！

上网搜了下别人的write up发现原来flag是原来输出的MD5哈希值...也就是说直接运行源程序的输出就是flag

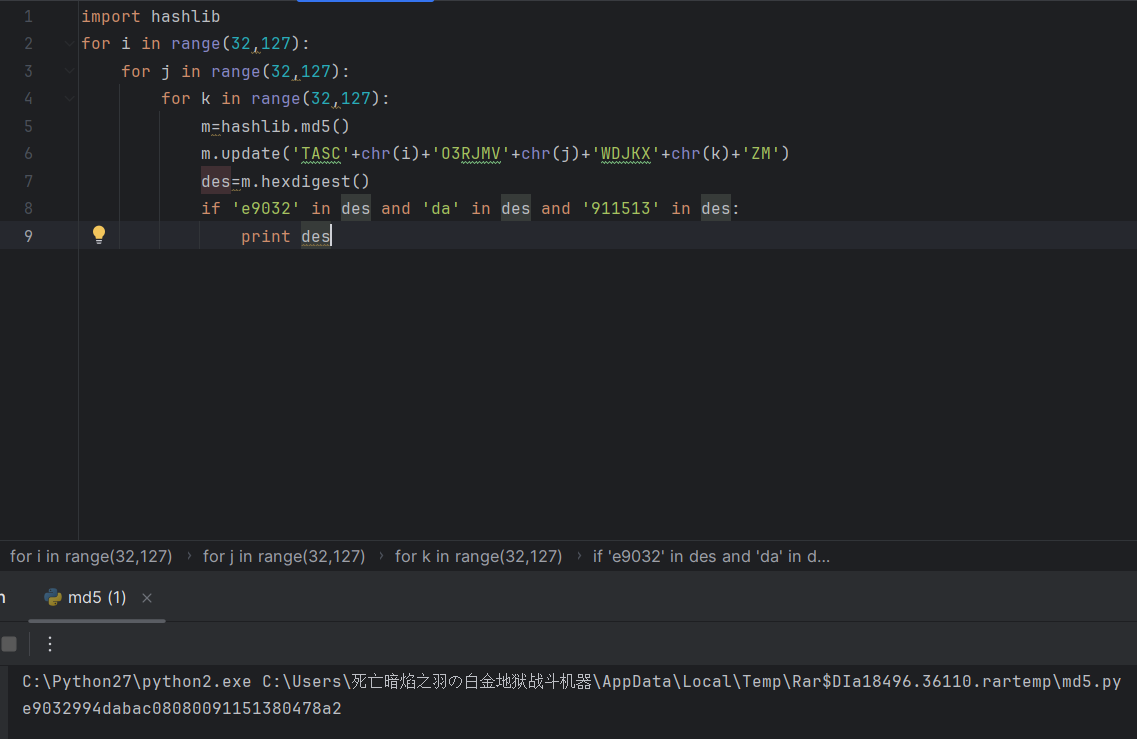
考点：会运行python文件……

Alice与Bob（RSA）

题目介绍如图：

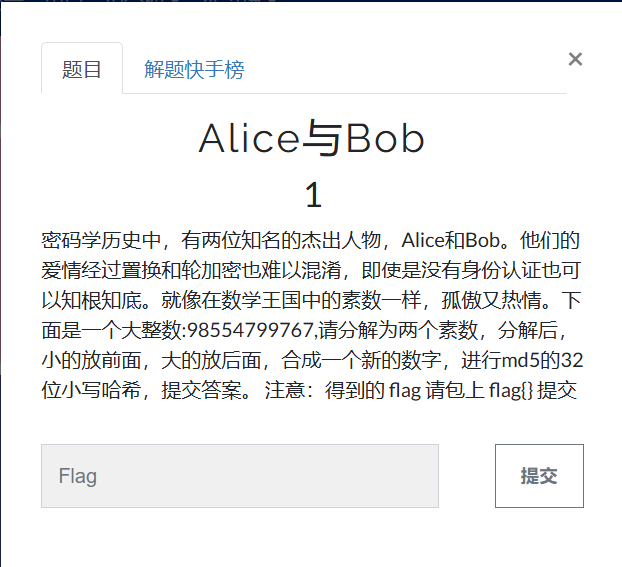
我们根据之前学的RSA算法，在这题中可以设n=98554799767，我们要求解的就是素数p、q的值

大整数分解

大整数分解非常消耗算力，目前仍是世界级难题，是非常重要的研究方向，其有很多种算法，性能上各有差异，这里不做赘述

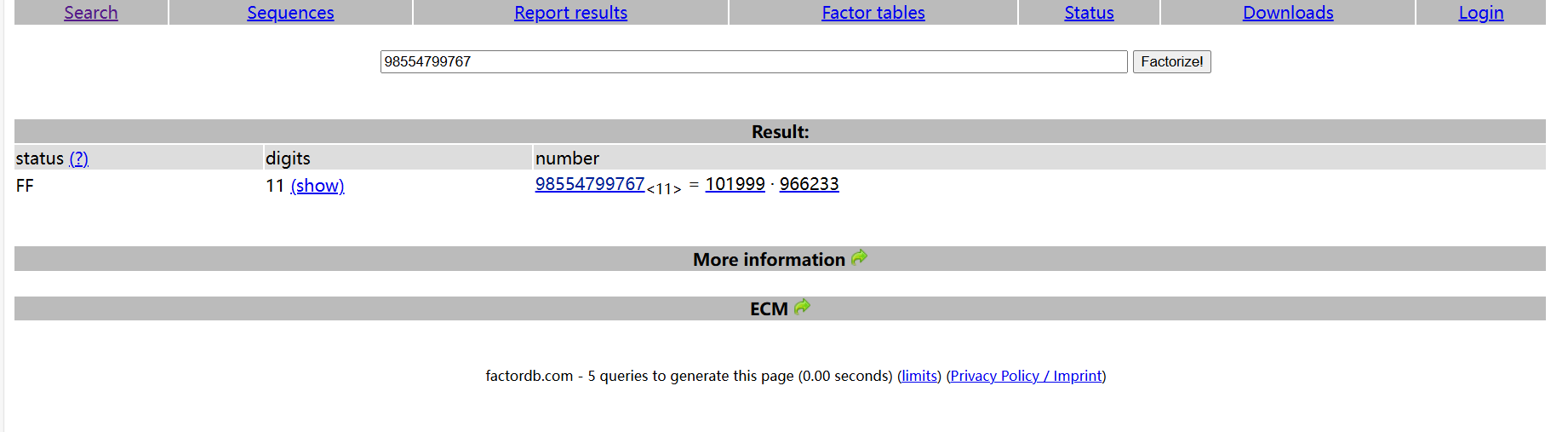
我们可以使用在线大整数分解网站：factordb.com

Factordb

Factordb 的核心是一个质因数数据库。当用户输入一个整数时，系统首先会在数据库中检查该数是否已经被分解过。如果数据库中有现成的分解结果，Factordb 会直接返回结果，而不需要进行新的计算；如果数据库中没有现成的分解结果，Factordb 可以将计算任务分配到不同的服务器或节点上进行并行计算。这使得它能够处理许多需要大量计算资源的分解任务。

我们可以直接在线分解出素数p、q的值：

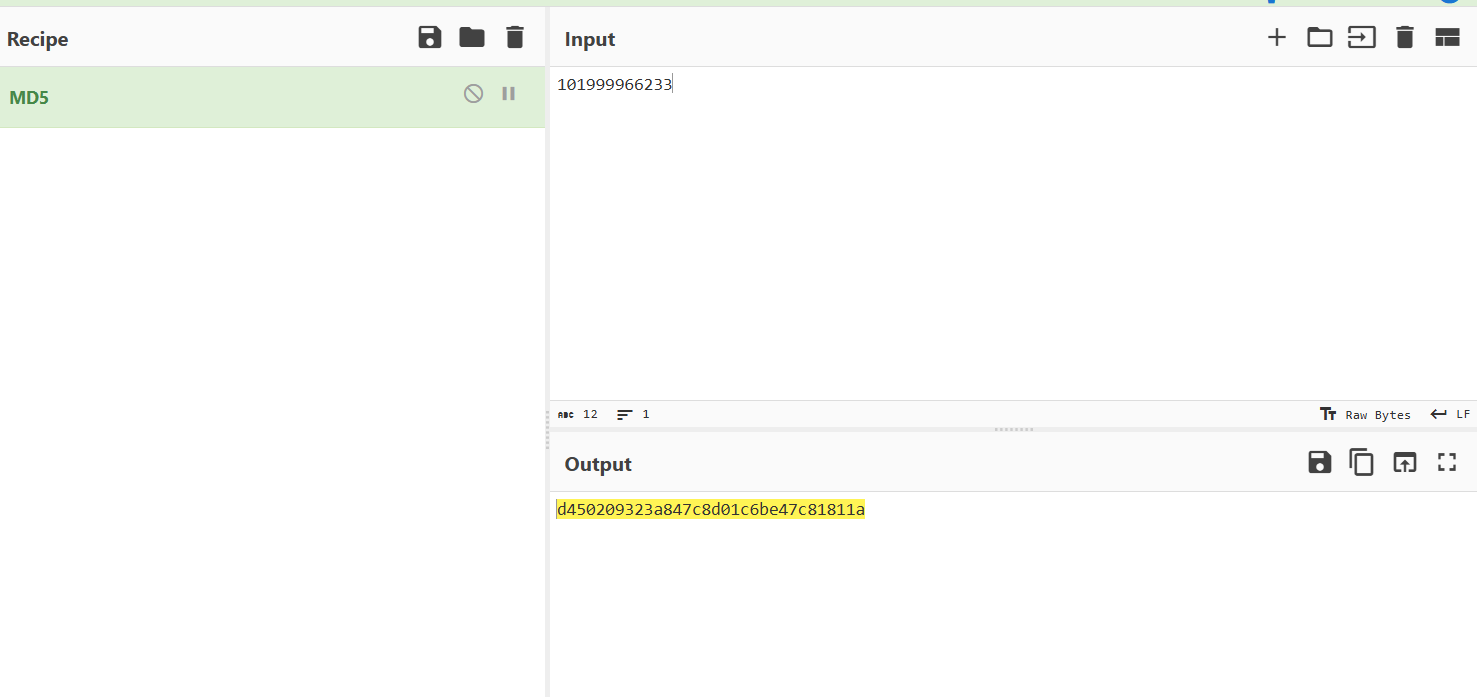
按照题目要求将两个数字组合进行MD5加密，即可得到flag：

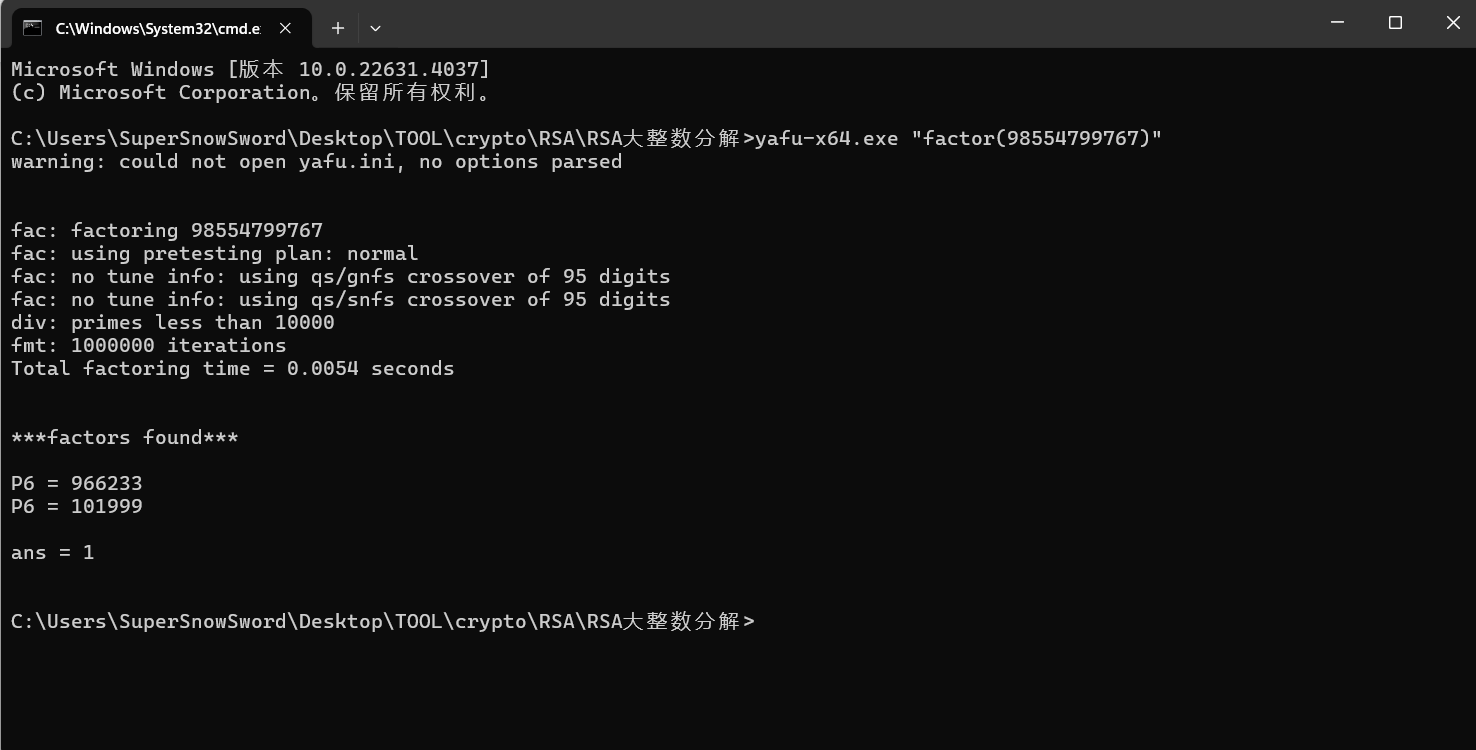
补充：使用工具yafu进行大整数分解

YAFU（Yet Another Factoring Utility）是一个用于整数分解和素数检测的开源工具，专为处理大整数而设计，能够快速有效地分解各种规模的整数。它主要用于数学研究、密码学分析以及与质因数相关的问题。YAFU 在分解过程中结合了多种高效的算法，并支持自动选择最佳算法来处理不同大小的整数。

我们可以使用以下命令：

yafu-x64.exe "factor(98554799767)"

或者将大整数的值放入1.txt中，使用以下命令：

yafu-x64.exe "factor(@)" -batchfile 1.txt

考点：大整数分解

大帝的密码武器（知识巩固题）

下载文件，发现是一个没有后缀名的文件，我们优先使用010editor打开查看（010editor是什么：【CTF入门】BUUCTF Misc刷题（持续更新） - Super_Snow_Sword - 博客园 (cnblogs.com)）：

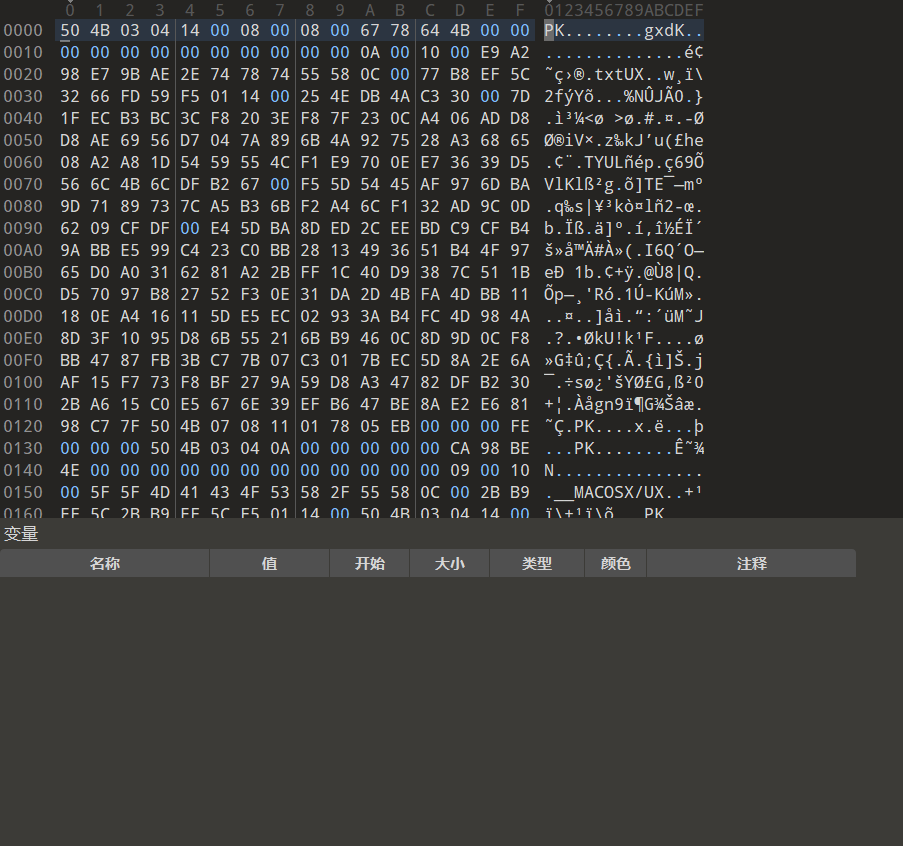
我们看见了zip的文件头，我们给它加上后缀打开得到了题目内容：

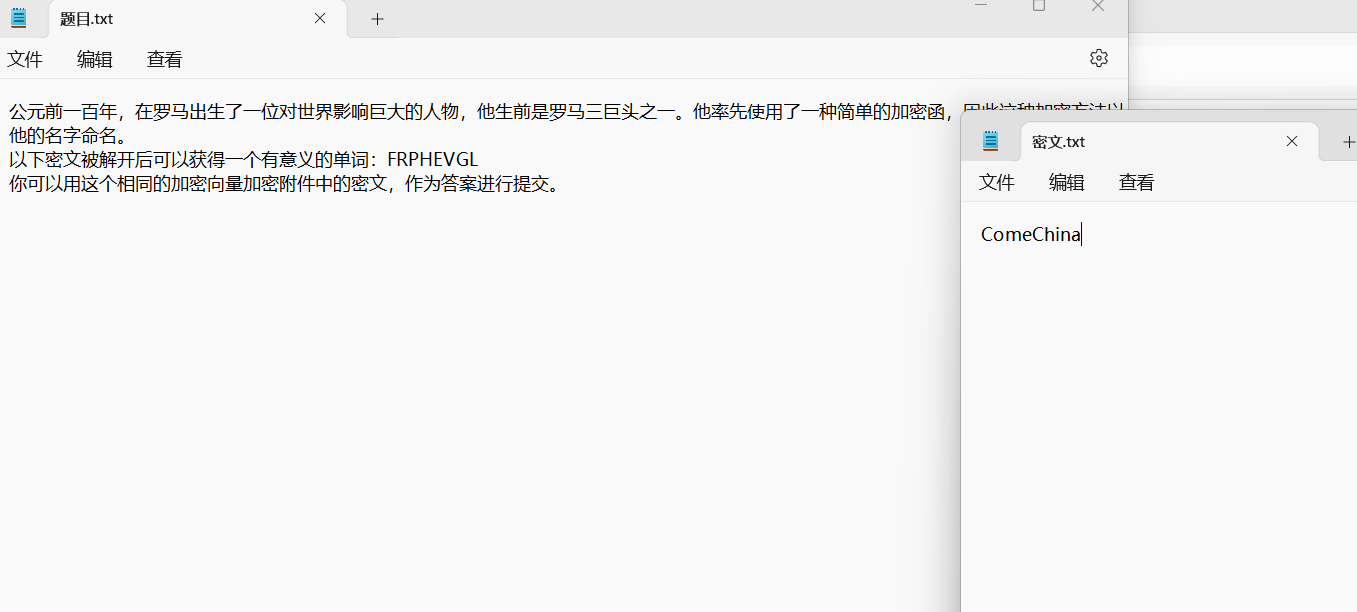
我们按照提示，对密文“FRPHEVGL”进行移位解密，即ROT13

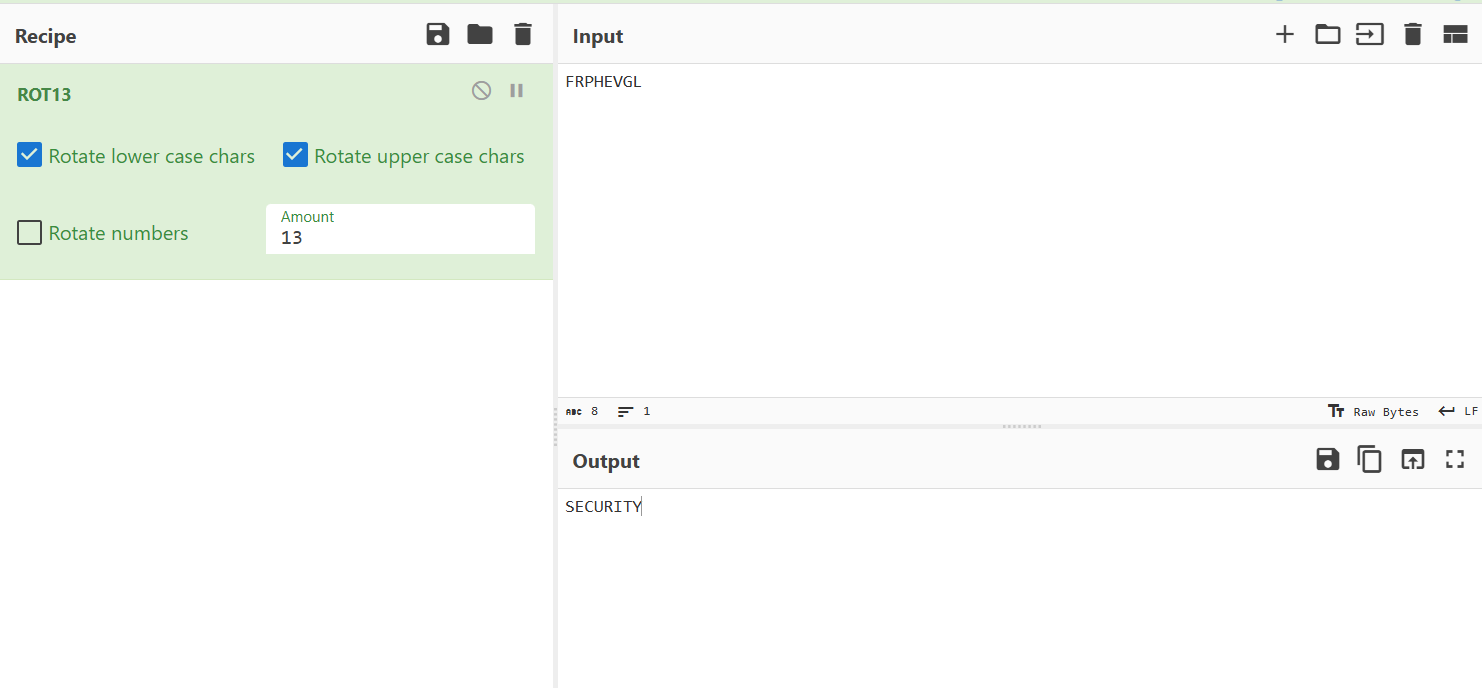
解出了明文SECURITY，加密向量即为13

我们使用相同的加密向量对密文“ComeChina”进行解密即可得到flag

考点：理解ROT13加密（凯撒密码）

rsarsa（RSA知识巩固题）

下载文件，打开发现：

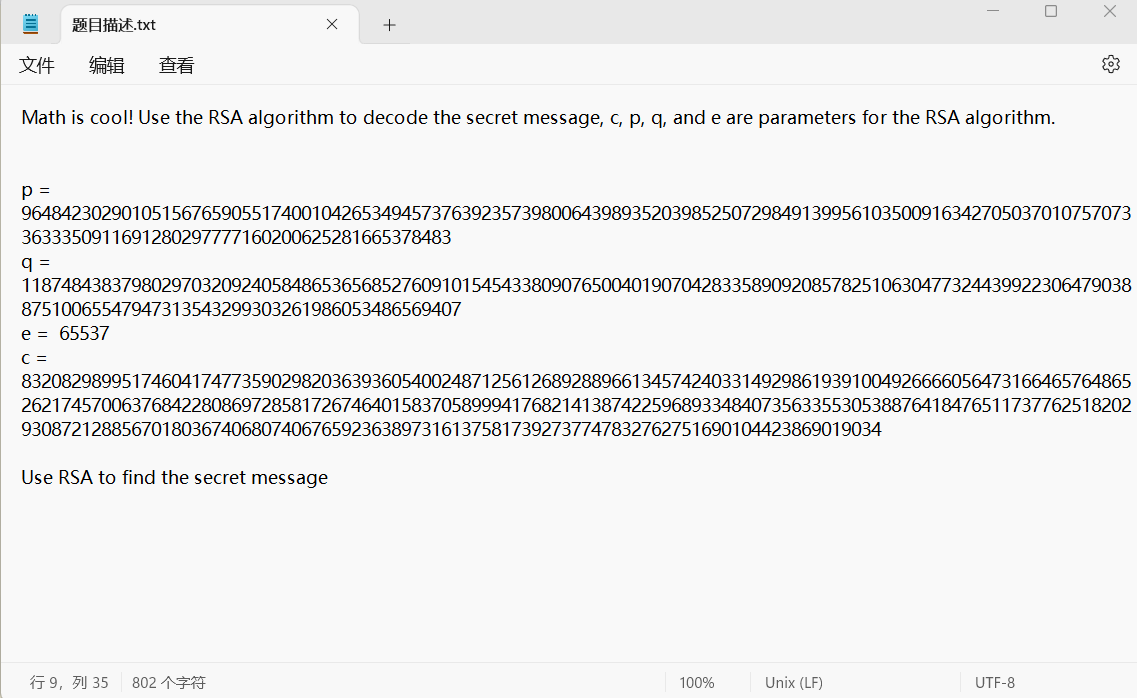
按照题目提示，这道题目给了我们RSA算法所需的参数来用于解密密文c

参数充足，说明我们可以直接计算出明文，现在仍可以使用之前脚本：

c = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034
p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e = 65537
n = p*q
phi = (p-1)*(q-1)
d = pow(e,-1,phi)
m = pow(c,d,n)
print(m)

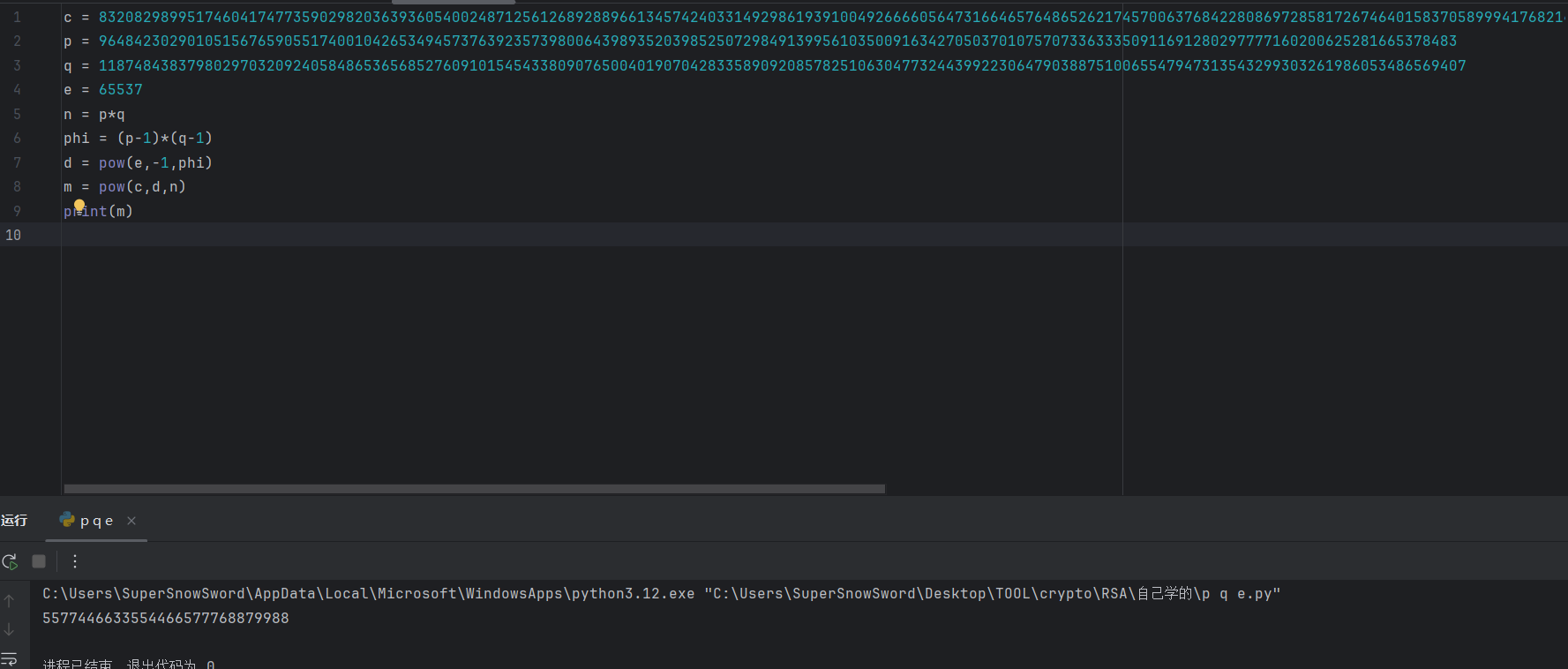
我们可以得出明文m的值为5577446633554466577768879988

即为我们的flag

考点：理解RSA加密原理并运用p、q、e、c计算出m

Windows系统密码

下载文件，打开发现：

这是Windows 系统中存储用户密码哈希值的常见格式，可能是通过工具（如 pwdump 或 hashdump）提取出来的。这是典型的 Windows 本地账户密码哈希格式，包含用户信息、LM 哈希和 NT 哈希。我们逐一进行分析：

第一个用户
用户名：Administrator
用户RID：500	用于标识用户账号
LM哈希：aad3b435b51404eeaad3b435b51404ee	LM（LAN Manager）哈希，用于表示空密码或 LM 哈希被禁用的情况，我们解密得到的值为空
NT哈希：31d6cfe0d16ae931b73c59d7e0c089c0	NT（NTLM）哈希，用于表示实际密码的NT哈希值，我们解密得到的值为空
综上所述，这是一个Administrator账户密码为空的情况

第二个用户
用户名：ctf
用户RID：1002
LM哈希：06af9108f2e1fecf144e2e8adef09efd	解密得到的值为GooD-LucK或Good-Luck或good-luck或GOOD-LUCK或Good-LucK或Good-luck
NT哈希：a7fcb22a88038f35a8f39d503e7f0062	解密得到的值为good-luck
综上所述，这是一个ctf账户密码为good-luck的情况

第三个用户第四个用户同第一个用户

因此我们可以猜测flag为ctf用户的密码

补充：LM哈希和NT哈希

LM 哈希用于 Windows 早期版本，是一种不安全的哈希算法。它将用户密码转换为大写（这也导致了LM哈希对大小写不敏感），并截断到 14 个字符，再使用 DES（数据加密标准）算法加密。

NT Hash 是基于 MD4 算法计算出的哈希值，密码以 Unicode 形式输入并进行哈希处理。这种哈希算法比 LM Hash 更安全，但仍然容易受到暴力破解的威胁，特别是对于弱密码。

考点：理解windows系统密码的格式、hash系列算法解密

信息化时代的步伐（新编码）

下载文件，打开发现：

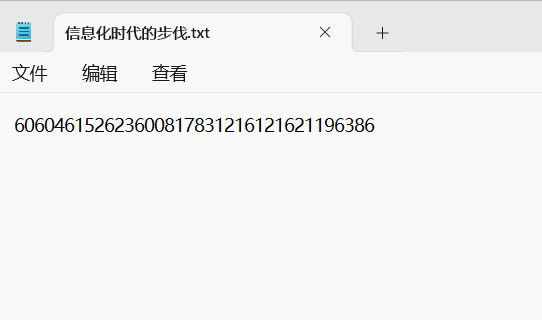
根据题目提示，这是经过中文电码编码的内容，我们直接进行解密即可得到flag（中文电码是什么：【CTF入门】BUUCTF Misc刷题（持续更新） - Super_Snow_Sword - 博客园 (cnblogs.com)）：

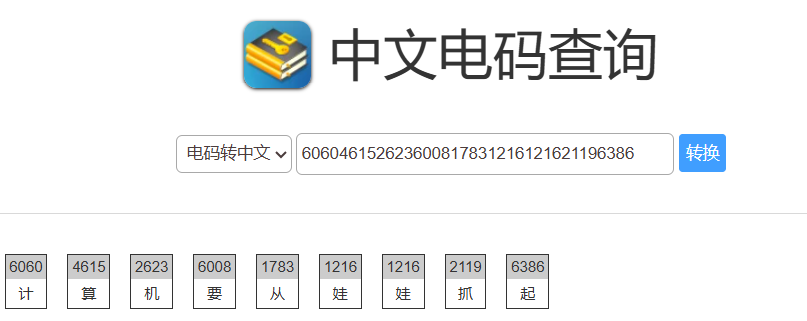
考点：理解中文电码

凯撒？替换？呵呵!（新密码）

题目介绍如图：

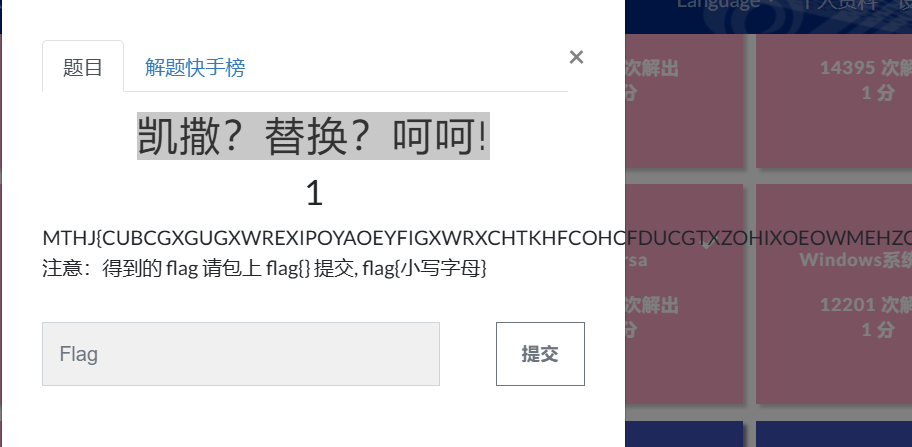
我们尝试使用ROT13对密文进行解密，发现并没有什么用

按照题目名提示，这一次的替换密码可不是凯撒密码那种简单的按照顺序的替换了，而是不规则的替换：

凯撒密码规则替换：
M——Z
T——G
H——U
J——W
不规则的替换：
M——F
T——L
H——A
J——G

我们只能推测前四个字符的不规则替换，其他字符该怎么办呢？

在此我们可以使用在线网站quipqiup - cryptoquip and cryptogram solver进行不规则替换的自动匹配

不规则替换密码自动匹配的原理

替换密码最经典的破解方法是频率分析。在自然语言中，不同字母出现的频率是有规律的。例如，在英语中，字母 E 是最常用的字母，出现频率最高。Quipqiup 会先对密文进行字母频率统计，并将这些统计数据与常见语言的字母频率进行比较，以猜测每个字母可能的替换。

我们打开网站，输入密文，再将一些我们可以确定的替换输入到线索框中以提高准确率：

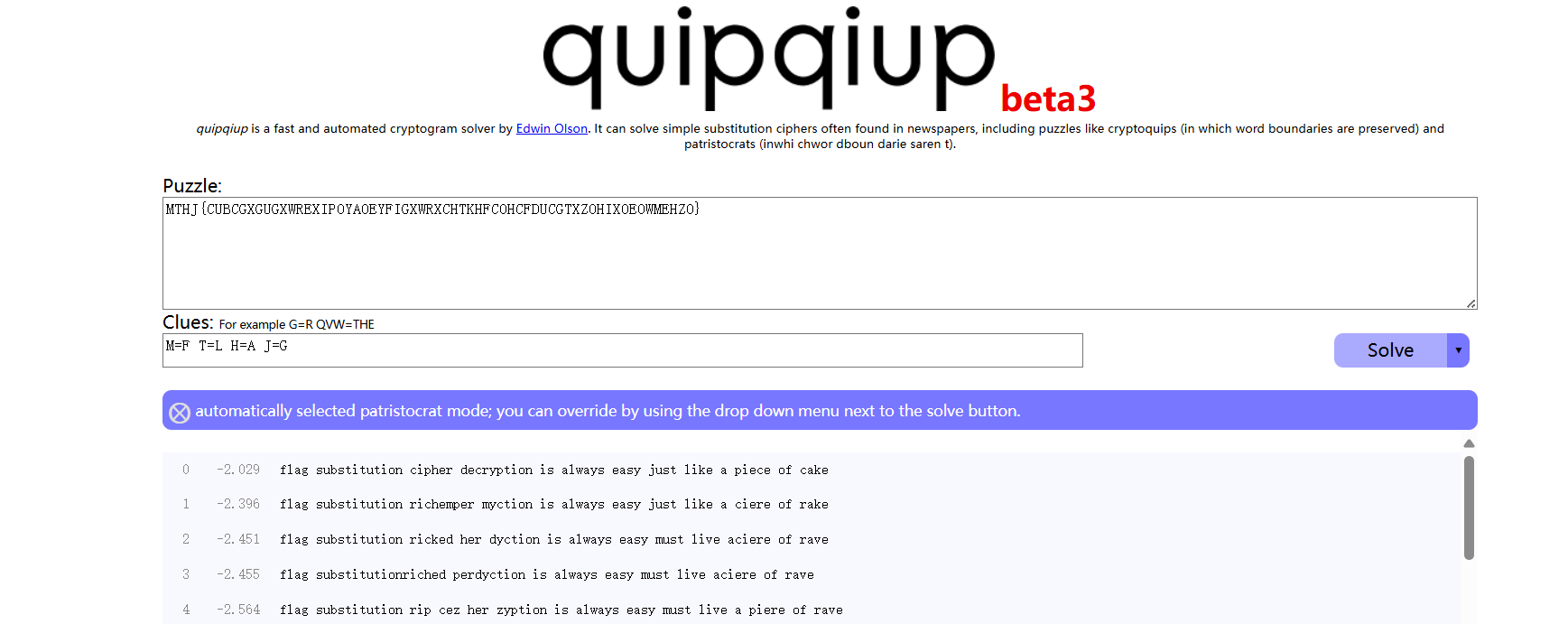
我们得到了flag

考点：理解替换密码、理解字频分析

萌萌哒的八戒（新密码）

下载文件，是一张图片：

根据题目提示到了“猪”，能够推测出这是猪圈密码

猪圈密码

一种简单的替代密码。在这种密码中，字母用特殊符号或图案代替，使信息更加隐秘。这个密码的名字来源于其加密字母表的网格或栅栏结构，看上去类似于猪圈或栅栏。

在此我们可以对照表格来进行解密，也可以使用在线工具（）得到flag：

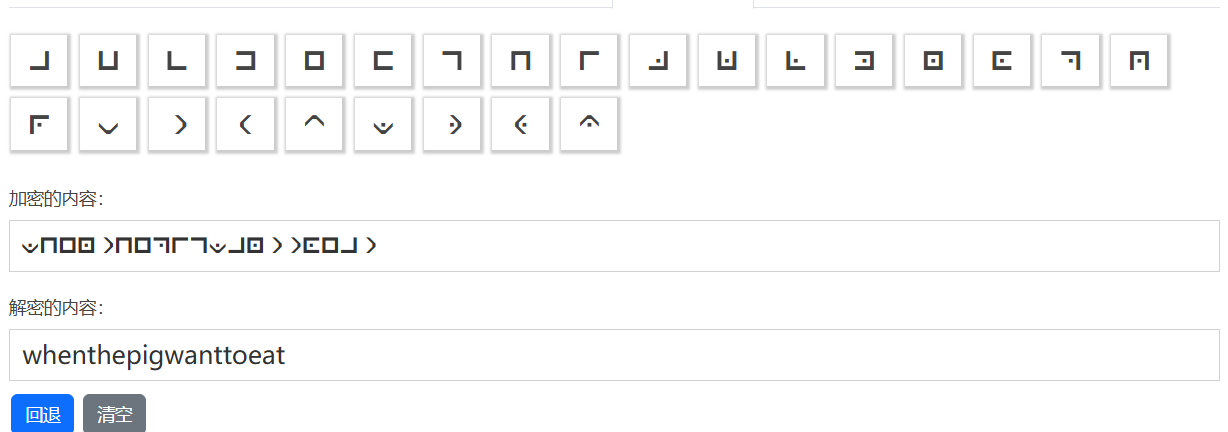
考点：理解猪圈密码

权限获得第一步（知识巩固题）

下载文件，是只有一段字符串的txt文件：

这是Windows 系统中存储用户密码哈希值的常见格式

我们可以直接进行解密：

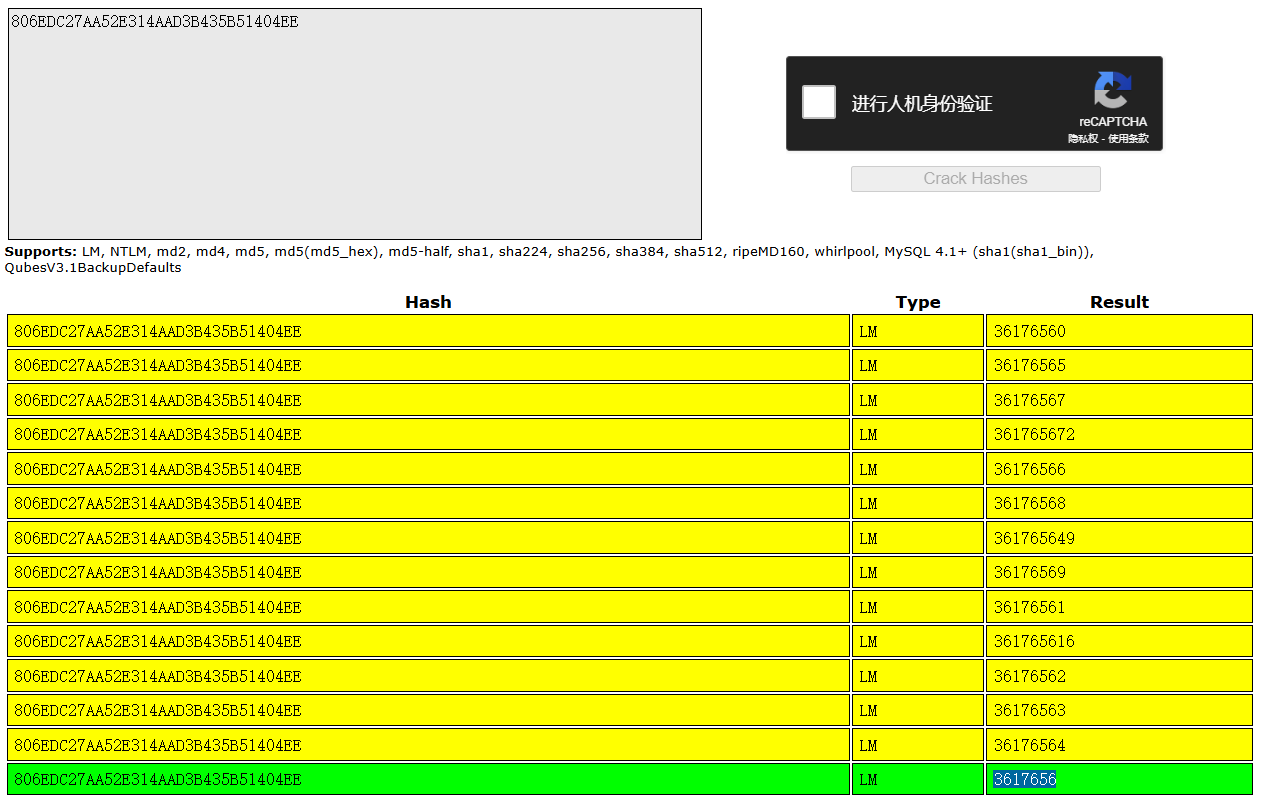
LM哈希和NT哈希值一致，说明3617656为正确的密码

考点：理解windows系统密码的格式、hash系列算法解密

RSA1（新RSA）

下载文件，是RSA加密泄露的数据与密文：

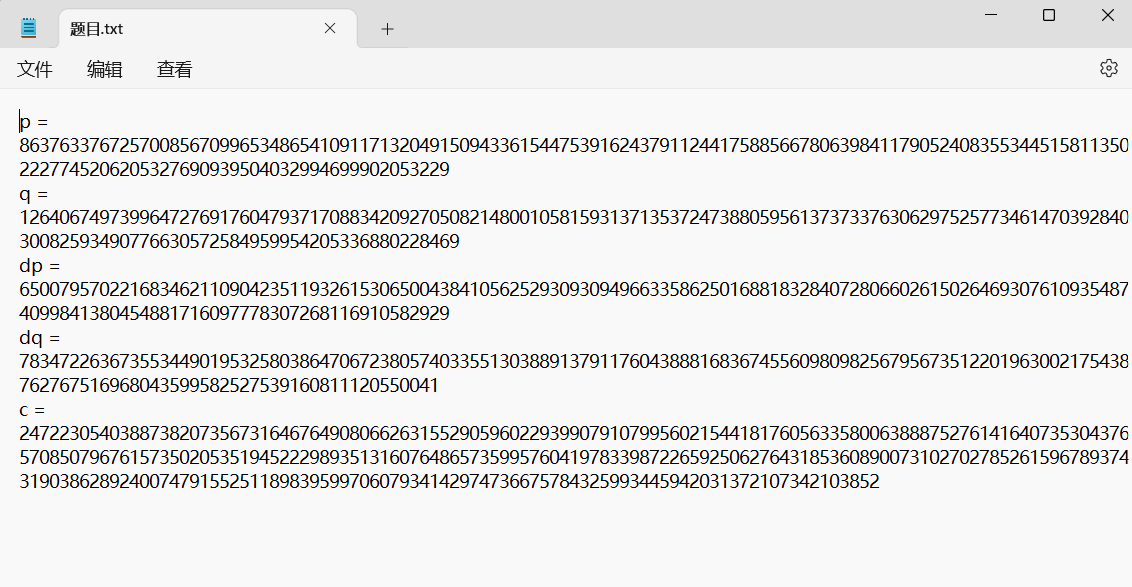
这一次，我们遇到了从未见过的dp和dq数据，这是什么？

dp是私钥d与(p-1)取余的值，即dp = d%(p-1)

同理dq = d%(q-1)

（以下内容参考文章：RSA加密算法详细解说_rsa算法-CSDN博客）

（前置知识：中国剩余定理https://www.bilibili.com/video/BV1jY4y1a7bK?vd_source=69c558b0c7be97607c79afbd75bd1f7c

费马小定理https://www.bilibili.com/video/BV1u2421c7v3?vd_source=69c558b0c7be97607c79afbd75bd1f7c）

相当于这一次我们拥有两个私钥dp和dq，利用中国剩余定理有：

m1 ≡ C^d mod p
m2 ≡ C^d mod q

证：
∵	m ≡ C^d mod n
∴	m ≡ C^d + k*n
	即m ≡ C^d + k*p*q
上式两遍同时取余p和q即可得到
m1 ≡ C^d mod p
m2 ≡ C^d mod q
其中
m1 = m mod p
m2 = m mod q

由此我们有：

C^d = k*p + m1	①
m2 ≡ (k*p + m1) mod q
上式两边同时减去m1有
m2 - m1 ≡ k*p mod q
上式两边同时除q有
(m2 - m1)/p ≡ k mod q
k ≡ (m2 - m1)/p mod q	②

①②式合并有

C^d = [(m2 - m1)/p mod q]*p + m1

只要能够求出m1和m2我们即可得出C^d的值

∵	dp = d%(p-1)	dq = d%(q-1)
∴	d ≡ dp mod(p-1)	d ≡ dq mod(q-1)
分别代入m1和m2有
m1 ≡ C^[dp mod(p-1)] mod p
m2 ≡ C^[dq mod(q-1)] mod q

用费马小定理推导：
假如p是质数，且gcd(k,p) = 1，则：k^(p-1) ≡ 1 mod p
∵	m1 ≡ C^[dp mod(p-1)] mod p
	dp mod(p-1) = dp + k*(p-1)
∴	m1 ≡ C^dp * C^[k*(p-1)] mod p
又∵	k^(p-1) ≡ 1 mod p
∴	C^[k*(p-1)] mod p = [C^(p-1) mod p]^k = 1^k = 1

我们就得到了最重要的公式（以上为证明过程）

m1 ≡ C^dp mod p
同理可得
m2 ≡ C^dq mod q

我们可以使用以下式子进行解密明文：

m = (((m1 - m2) * I) % p) * q + m2
I = q^(-1) mod p，即 q 关于 p 的模逆，是为了合并 m1 和 m2 的结果。

证明：
我们有以下两个同余关系:
m ≡ m1 mod p
m ≡ m2 mod q
中国剩余定理告诉我们，解m可以写成以下形式:
m = m1 + k1*p
m = m2 + k2*q
其中k1和k2是一个整数，需要通过m1和m2来确定。
接下来，我们需要通过m1和m2来计算k2，使得式子成立
代入到模数p的同余条件中:
m2 + k2*q = m1 mod p
k2*q = m1 - m2 mod p
因为q与p互素，我们可以乘以q在p下的模逆I，得到:
k2= (m1 - m2) *I mod p
于是：
k2= ((m1 - m2) * I) mod p
将k2带回到原来的表达式m =m2 + k2*q 中:
m = m2 + (((m1 - m2) * I) mod p) * q

因此，做这类题目我们需要理解的公式如下：

m1 ≡ C^dp mod p
m2 ≡ C^dq mod q
m = m2 + (((m1 - m2) * I) mod p) * q

在此我们给出解密脚本：

p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

import gmpy2
from Crypto.Util.number import long_to_bytes
I = gmpy2.invert(q,p)
m1 = pow(c,dp,p)
m2 = pow(c,dq,q)
m = (((m1-m2)*I)%p)*q+m2
print(long_to_bytes(m))

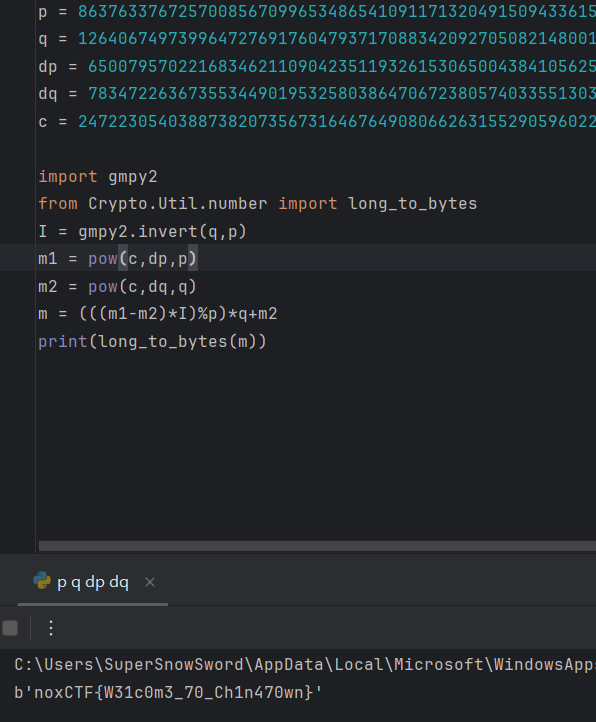
考点：理解RSA加密原理并运用c、p、q、dp、dq计算出m

传统知识+古典密码（新孬密码）

下载文件，题目内容如下：

可以发现年份使用的是六十甲子纪年的方式，一甲子即为六十年：

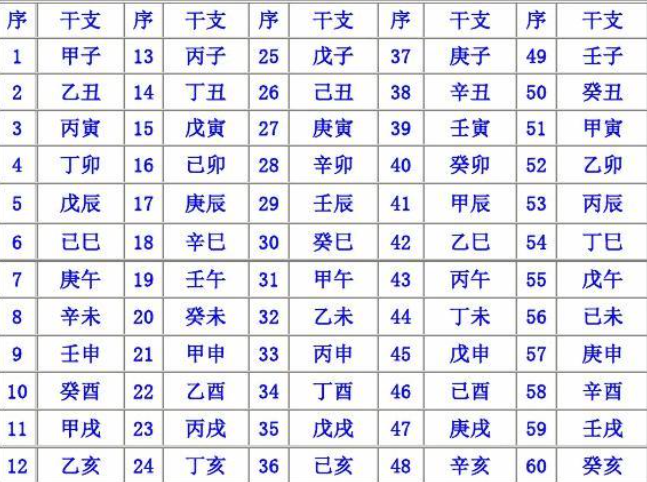
我们按照序号将六十甲子进行数字转换：

辛卯——28
癸巳——30
丙戌——23
辛未——8
庚辰——17
癸酉——10
己卯——16
癸巳——30
信的背面还写有“+甲子”，可能说明每个数字加上60，刚好可以进行ascii解码了

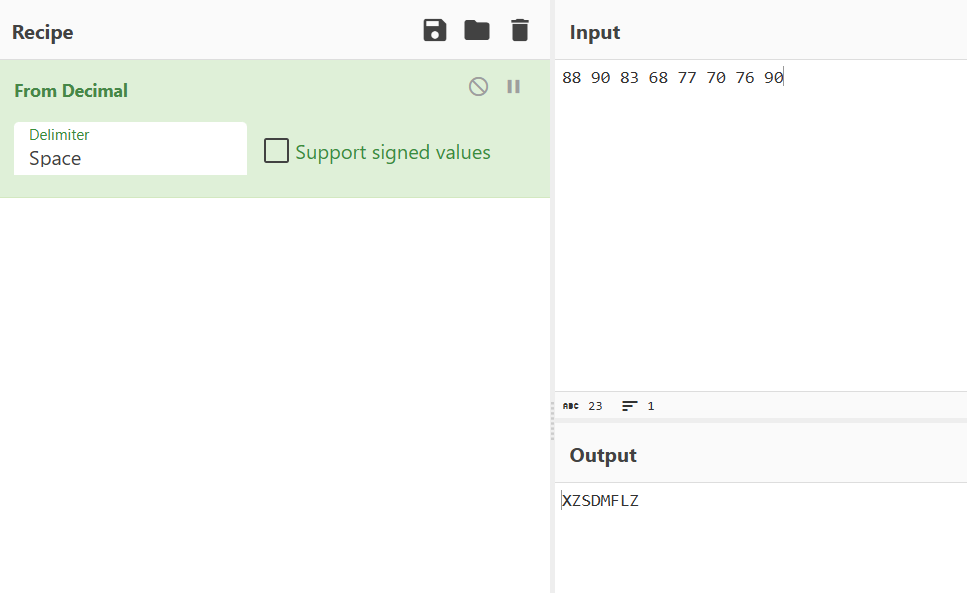
不是flag

题目有提示还有古典密码的部分，使用了凯撒密码爆破查看结果：

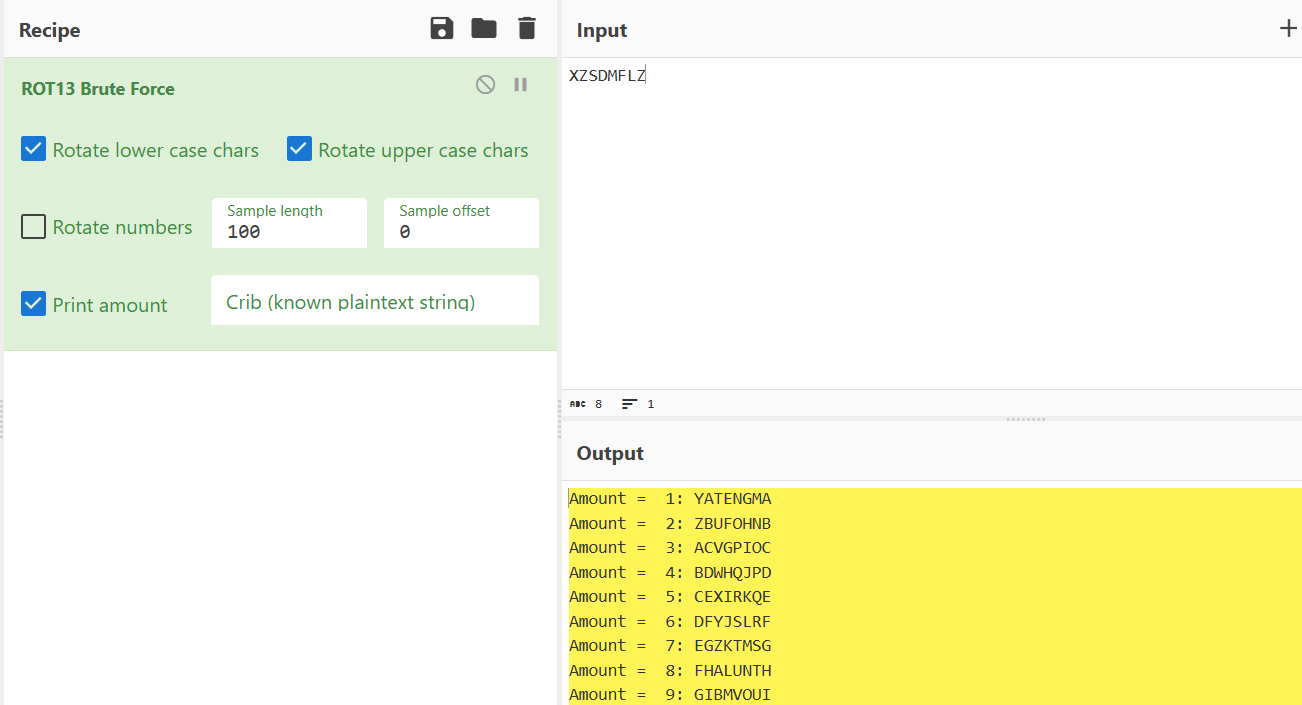
虽然看着很像但第一个结果并不是flag

看了网上的WP说是要用栅栏密码后再使用凯撒（提示太少了吧）：

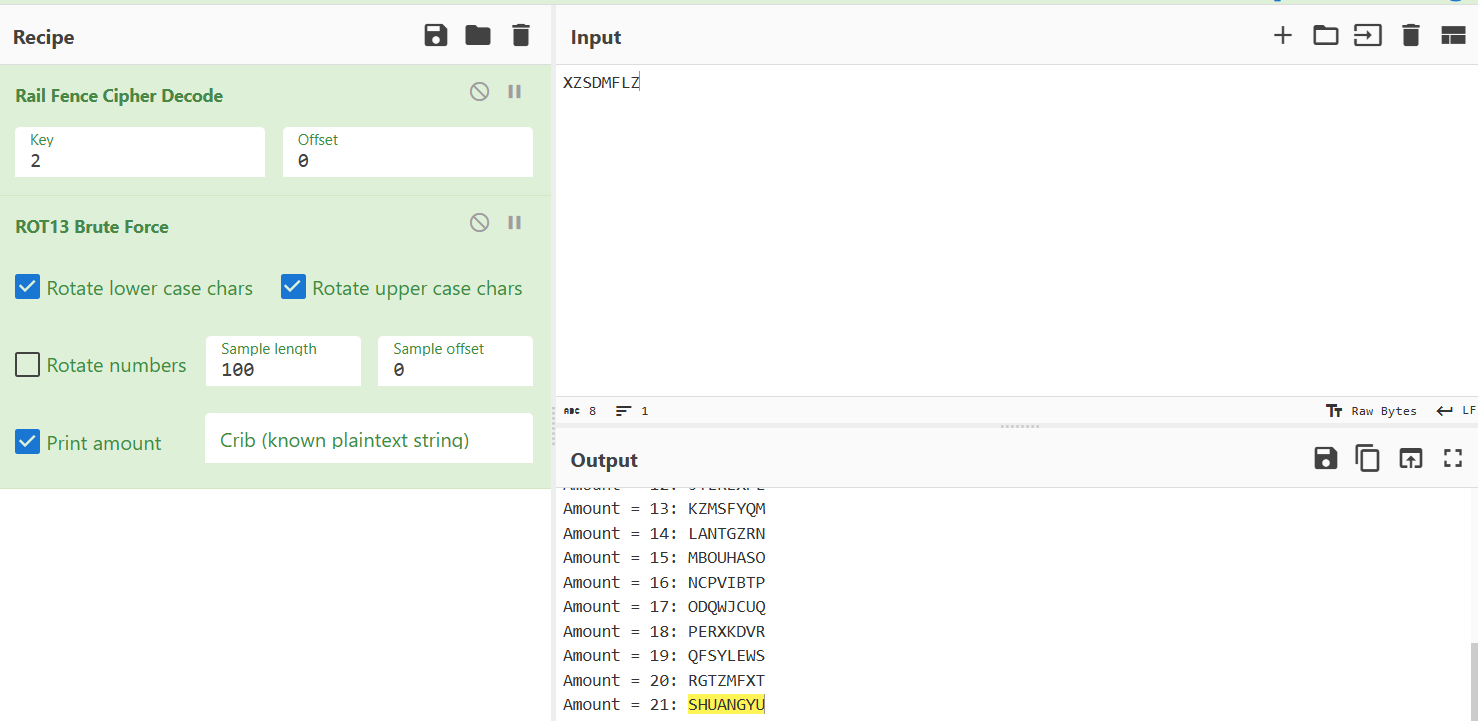
考点：理解六十甲子纪年方式

世上无难事（知识巩固题）

下载文件，是一串毫无规律的字母：

我们采用统计字频进行破解：

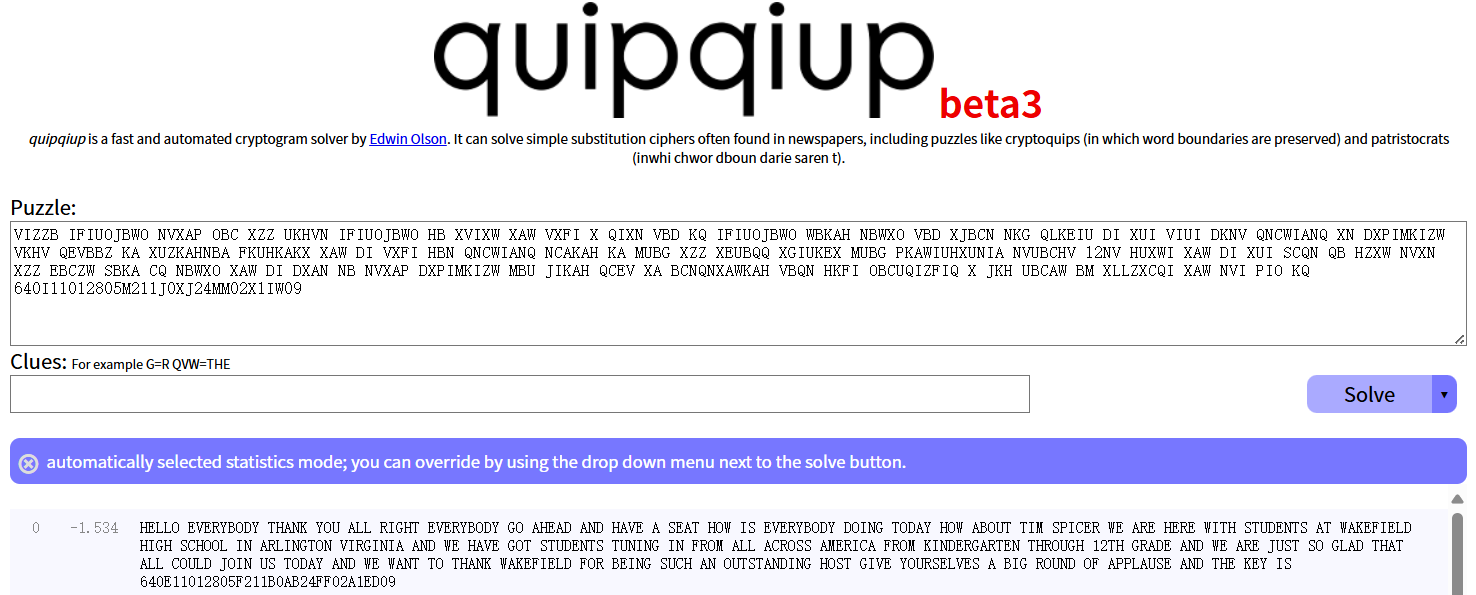
得到KEY，即为flag，按照题目提示我们要记得转换为小写

考点：理解字频分析

Unencode（新编码）

下载文件，是一串字符：

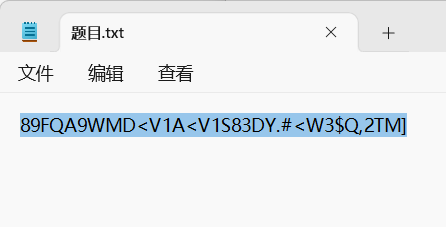
放入cyberchef，并没有反应，我们观察密文特征：

包含数字和字母
特殊字符包括了<.#$,]

我们可以尝试是否是UUencode的加密方式

UUencode

一种用于将二进制数据转换为可通过文本传输的 ASCII 编码的方式。它主要用于在早期的 Unix 系统之间通过电子邮件或其他文本传输协议传递二进制文件。这种编码格式的名字来源于 Unix 系统，它最早在 Unix 系统上用于实现计算机间的文件共享

特征：所有字符看起来像乱码，但都是可打印字符

得出flag：

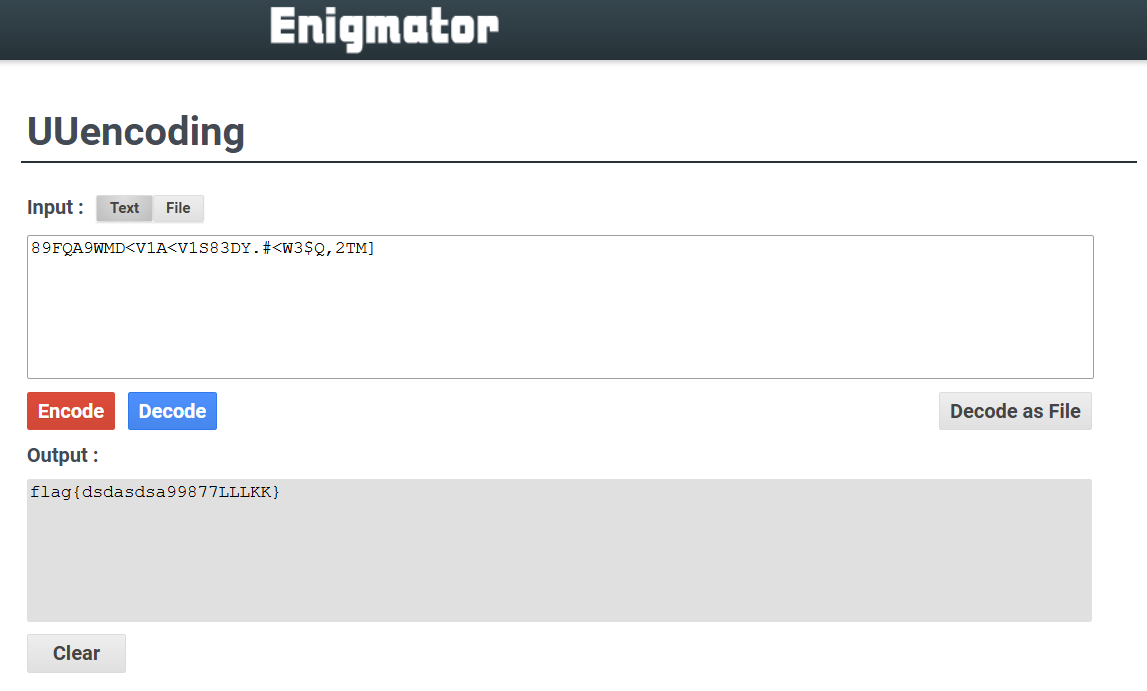
考点：理解UUencode

old-fashion（知识巩固题）

下载文件，是一看不懂的字符串：

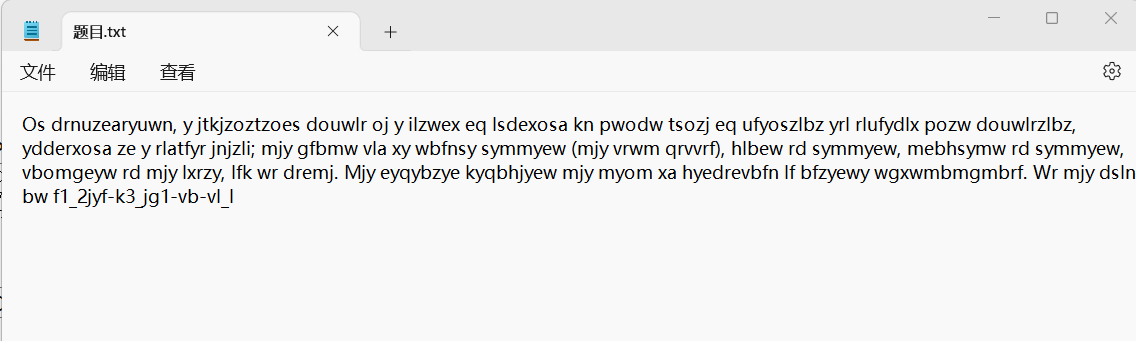
我们进行字频分析得到flag：

考点：理解字频分析

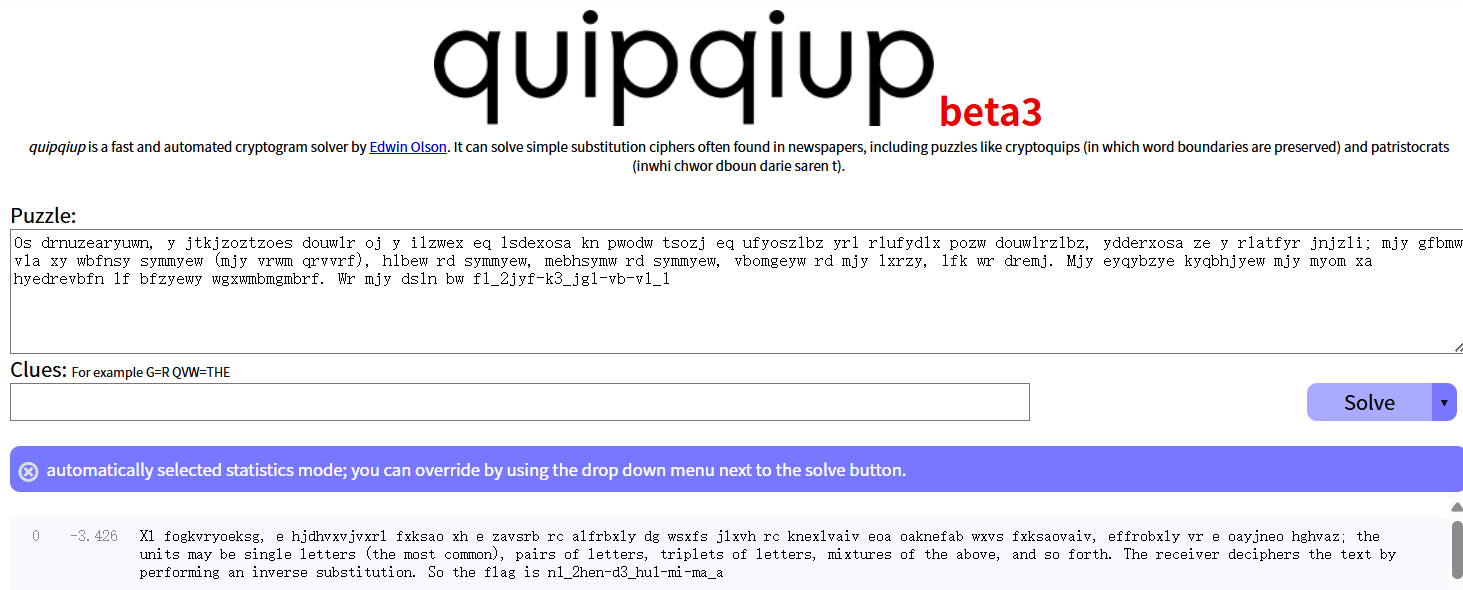
[AFCTF2018]Morse

摩斯电码不多说了

考点：知道摩斯电码加密

RSA3（新RSA）

下载文件，是RSA加密泄露的数据与密文：

我们可以发现这一次出现了两个密文c1和c2、两个公钥e1和e2，而两个公钥都是用同一个模数n

共模攻击

共模攻击是针对 RSA 加密的一种攻击方式，它的前提是不同的 RSA 公钥共享相同的模数 n，但使用不同的指数 e。具体来说，如果有两个密文 c1 和 c2 分别是使用不同的公钥（即 e1 和 e2），但相同的模数 n 加密的同一明文 m，那么就可以通过扩展欧几里得算法计算出明文 m。

https://www.bilibili.com/video/BV15K411t7Su?vd_source=69c558b0c7be97607c79afbd75bd1f7c

我们知道密文生成的公式：

c1 ≡ m^e1 mod n
c2 ≡ m^e2 mod n

明文m只有一串，但经过了两个不同的公钥生成了两个不同的密文，我们应该这样求m：

m ≡ c1^d1 mod n
m ≡ c2^d2 mod n

两个密钥e1和e2互素，则存在s1和s2使得：

e1*s1+e2*s2 = 1		#s1 和 s2是e1 和 e2 的最大公约数对应的系数

c1^s1*c2^s2 ≡ m^(e1*s1) * m^(e2*s2) mod n ≡ m^(e1*s1+e2*s2) ≡ m mod n

在不知道私钥的情况下我们可以得出明文m：

m =  (c1^s1 * c2^s2) mod n

因此我们可以编写以下脚本：

from Crypto.Util.number import long_to_bytes
from gmpy2 import gcdext

c1=22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
n=22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
e1=11187289
c2=18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397
e2=9647291

_,s1,s2 = gcdext(e1,e2)	#根据扩展欧几里得算法求出s1和s2，满足e1*s1+e2*s2 = 1。前方加上一个“_”说明我们忽略gcdext(e1,e2)返回的第一个值——最大公约数

m = pow(c1,s1,n) * pow(c2,s2,n) % n

print(long_to_bytes(m))

得出flag

考点：理解RSA共模攻击原理并运用c1、c2、n、e1、e2计算出m

RSA2

下载文件，是RSA加密泄露的数据与密文：

我们可以发现这一次我们能用的只有泄露的dp和公钥

dp泄露

∵dp ≡ d mod (p-1)
∴d = dp + k1 * (p-1)

又∵d ≡ e^-1 mod[(p-1)*(q-1)]
∴d * e = 1 + k2(p-1)(q-1)

则	(dp + k1(p-1)) * e = 1 + k2(p-1)(q-1)

    e * dp mod (p - 1) ≡ 1	#两边同时对(p-1)取模，消去k
    e * dp = 1 + k(p - 1)

之后我们需要通过爆破k（k的范围为1~e）的方式求出p，进而求出d

因此我们可以编写以下脚本：

from Crypto.Util.number import long_to_bytes
e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657
c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751

for k in range(1,e):
    if (dp * e - 1) % k == 0:   #判断k是否能够整除得出p-1
        if n % (((dp * e - 1) // k) + 1) == 0:  #判断n能否被得到的p整除
            p = ((dp * e - 1) // k) + 1
            q = n // p
            d =  pow(e,-1,(p-1)*(q-1))

m = pow(c,d,n)
print(long_to_bytes(m))

得出flag

考点：理解RSAdp泄露原理并运用c、e、n、dp计算出m

还原大师（知识巩固题）

题目概述：

可以看出这题考点是MD5碰撞

我们可以利用之前的脚本，而且都不用修改。。。：

import hashlib	#导入hashlib库：这个库提供了多种哈希算法，如MD5、SHA-1等，用于生成数据的哈希值。
for i in range(32,127):
    for j in range(32,127):
        for k in range(32,127):
            m=hashlib.md5()	# 创建一个新的MD5对象
            m.update('TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM')	# 嵌套循环生成字符串，并计算字符串的MD5哈希值
            des=m.hexdigest()	#获取哈希值的十六进制表示
            if 'e9032' in des and 'da' in des and '911513' in des:	#检查哈希值是否包含指定的字符串
                print des	#输出哈希值

再按照题目要求将输出经MD5加密即可得到flag

考点：理解MD5碰撞

异性相吸（新加密脑洞）

下载文件，里面有密文和密钥的两个文件：

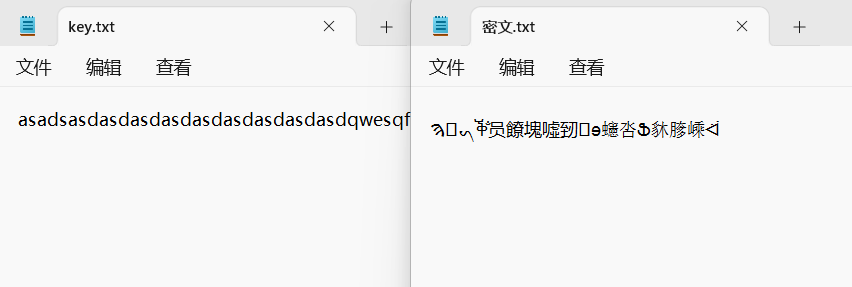
密文是乱码，我们使用010 editor进行分析查看：

我们可以发现密文和密钥文件内容长度相同，因此可能是逐个字符加密的加密方式

题目提示“异性相吸”，因此我们可以先尝试异或加密的方式

异或加密

异或加密（XOR Encryption）是一种简单的对称加密方法，使用逻辑运算中的异或（XOR）操作来加密和解密数据。

https://www.bilibili.com/video/BV1qW4y1L7tN?vd_source=69c558b0c7be97607c79afbd75bd1f7c

我们以二进制的方式查看密文和密钥，提取进行异或操作

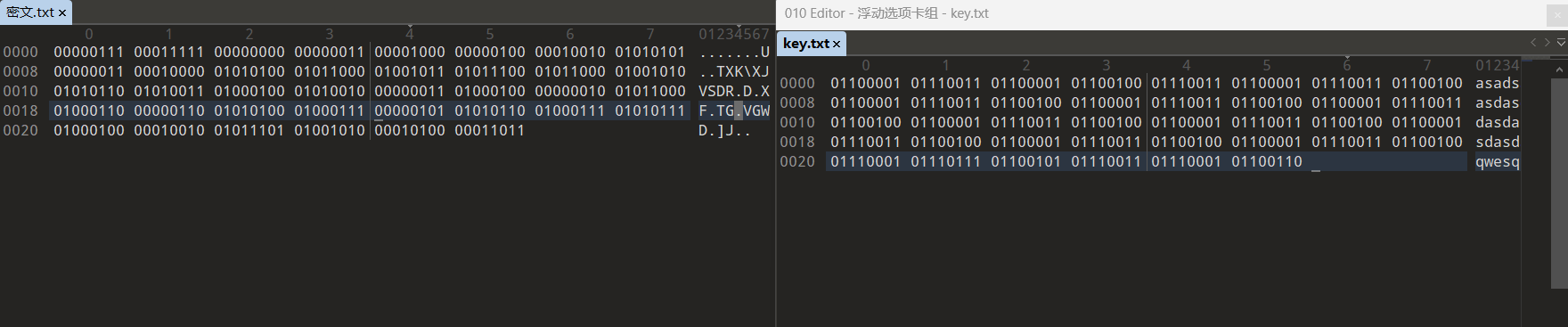
异或脚本：

a = '0110000101110011011000010110010001110011011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011100010111011101100101011100110111000101100110'
b = '0000011100011111000000000000001100001000000001000001001001010101000000110001000001010100010110000100101101011100010110000100101001010110010100110100010001010010000000110100010000000010010110000100011000000110010101000100011100000101010101100100011101010111010001000001001001011101010010100001010000011011'
c = ''

for i in range(len(a)):
    if(a[i] == b[i]):
        c+='0'
    else:
        c+='1'
print(c)

得到flag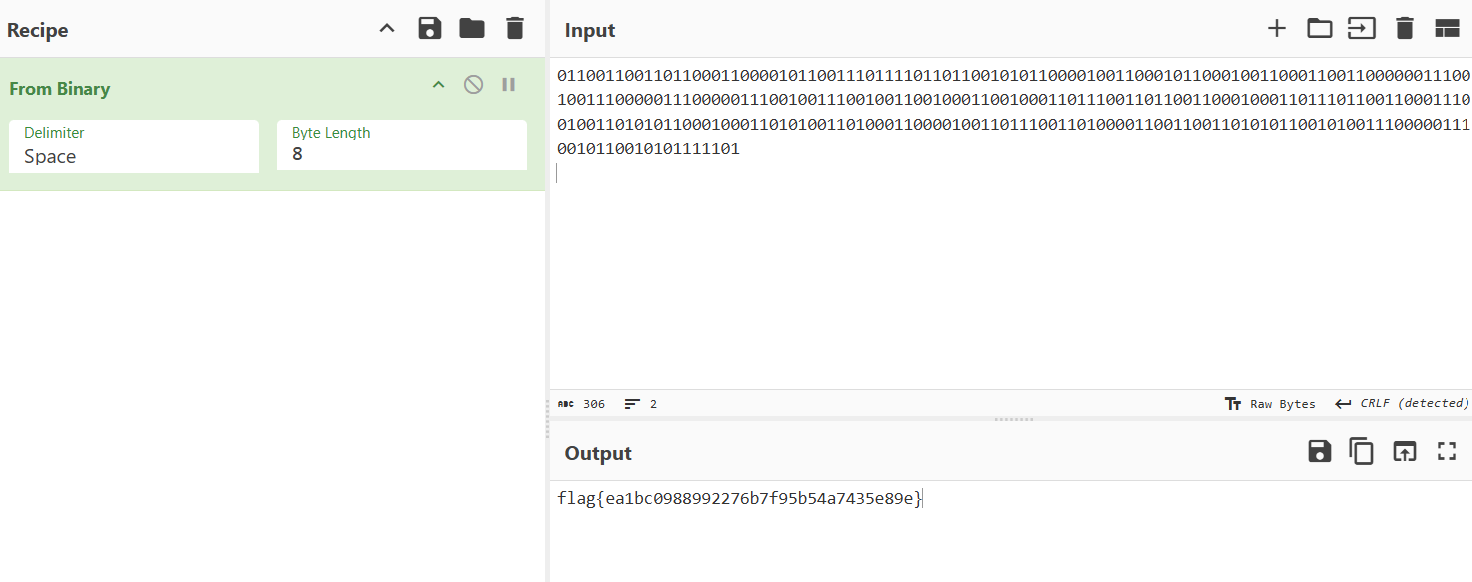

考点：理解异或加密

RSA（新RSA）

下载文件，里面是一个密文文件enc和公钥文件key，我们使用010editor进行分析：

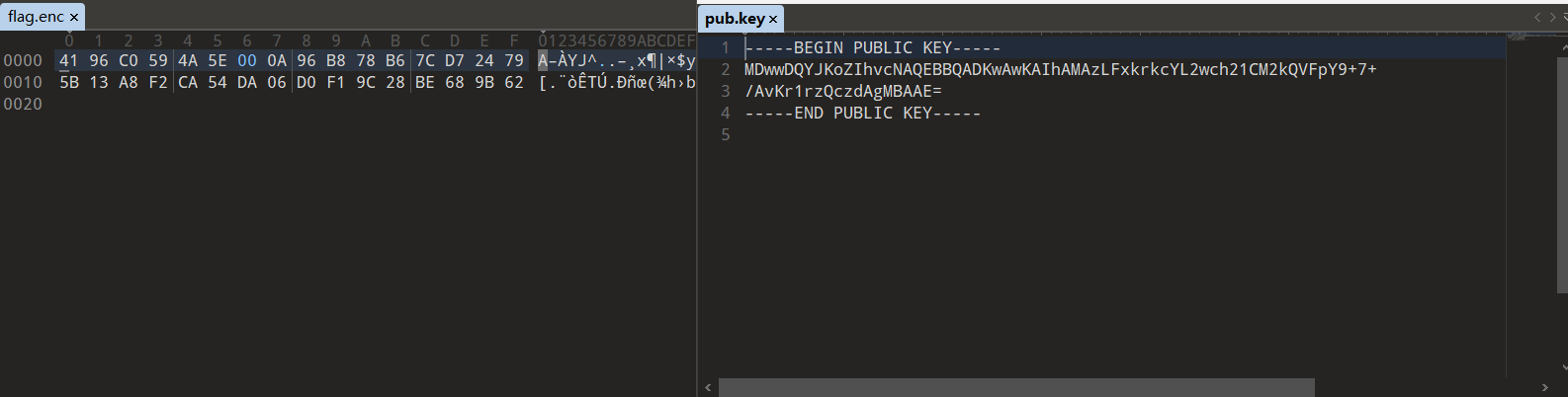
我们有了公钥文件，但这个公钥没有像往常一样直接给出e和n的值，这是怎么回事呢？

PEM格式

PEM（Privacy-Enhanced Mail）格式是一种用于编码和存储加密数据的文件格式。它通常用于传输和存储密钥、证书和其他安全信息。

在 PEM 格式中，公钥的 Base64 编码内容实际上是 ASN.1 格式的编码，描述了公钥的结构：算法标识（标识这是一个RSA公钥）、模数n和公钥指数e

那么我们想要从中得出模数n和公钥指数e又该怎么做呢？

公钥解析原理

公钥解析的原理主要基于对公钥格式（如 PEM、DER 等）的解析和解码，提取出公钥中的关键参数（如模数 nnn 和公钥指数 eee）。

1. 读取公钥文件

首先读取存储公钥的文件，通常是一个包含公钥的文本文件（如 PEM 格式）。对于 PEM 文件，它会去掉头尾的标识行（例如 -----BEGIN PUBLIC KEY----- 和 -----END PUBLIC KEY-----），并提取 Base64 编码的内容。

2. Base64 解码

提取出的 Base64 编码内容需要进行解码，将其转换为二进制数据。这个步骤的目的是将文本格式的数据还原为原始的二进制格式，以便进行进一步处理。

3. ASN.1 解码

许多公钥（尤其是 RSA 公钥）使用 ASN.1（抽象语法标记法）编码。ASN.1 是一种数据描述语言，用于定义数据结构。公钥的结构通常会包含：

公钥算法标识（例如 RSA）。
模数 n 和公钥指数 e。

使用 ASN.1 解码库（如 pyasn1 或 asn1tools）解析解码后的二进制数据，提取出这些参数。

4. 提取参数

通过 ASN.1 解码，解析工具能够提取出所需的公钥参数，包括：

模数 n：通常是一个很大的整数，表示为两个大素数 ppp 和 qqq 的乘积。
公钥指数 e：一个小的正整数，通常为 65537。

在此我使用了本地工具enigmator：

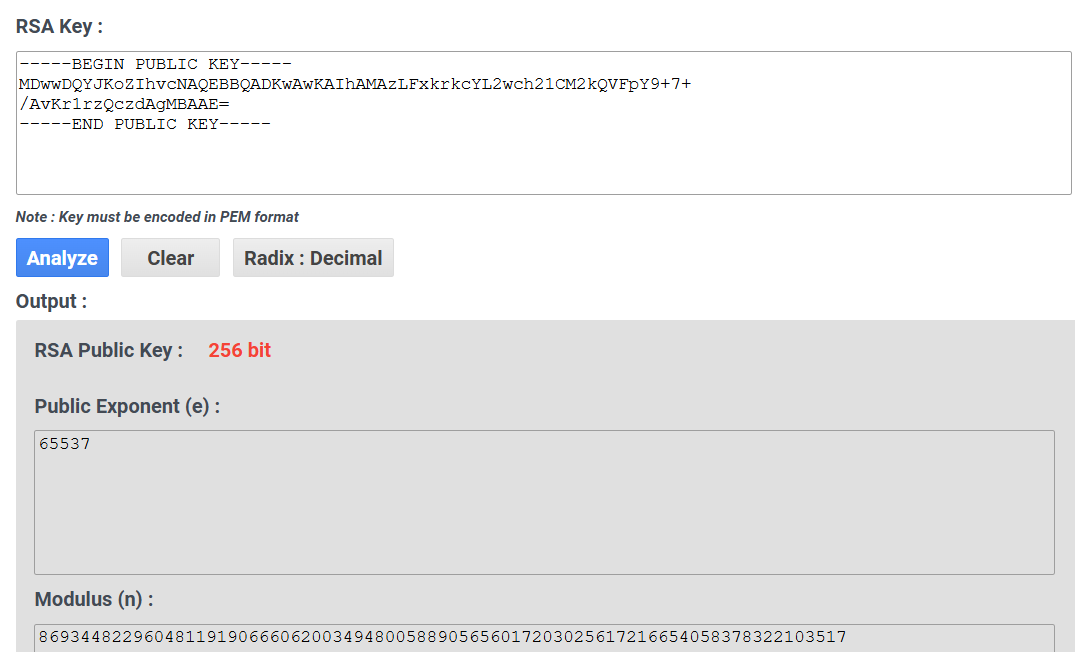
现在我们有了两个参数：

e = 65537
n = 86934482296048119190666062003494800588905656017203025617216654058378322103517

我们再进行大因数分解得出p和q：

e = 65537
n = 86934482296048119190666062003494800588905656017203025617216654058378322103517
p = 285960468890451637935629440372639283459
q = 304008741604601924494328155975272418463
d = pow(e,-1,(p-1)*(q-1))

有了这些值我们就可以解析密文了，密文为.enc文件，因此我们应该对其进行读取并进行解密

这里我们需要准备RSA解密的python模块，编写脚本如下：

import rsa

e = 65537
n = 86934482296048119190666062003494800588905656017203025617216654058378322103517
p = 285960468890451637935629440372639283459
q = 304008741604601924494328155975272418463
d = pow(e,-1,(p-1)*(q-1))

key = rsa.PrivateKey(n,e,d,q,p)	#生成私钥

with open("flag.enc","rb") as c:  #以二进制读模式，读取密文c
    c = c.read()
    print(rsa.decrypt(c,key))

得到了flag

考点：理解公钥解析原理、利用公钥文件计算出私钥、利用私钥分析密文文件

RSAROLL

下载文件，里面是一串奇怪的数字和提示：

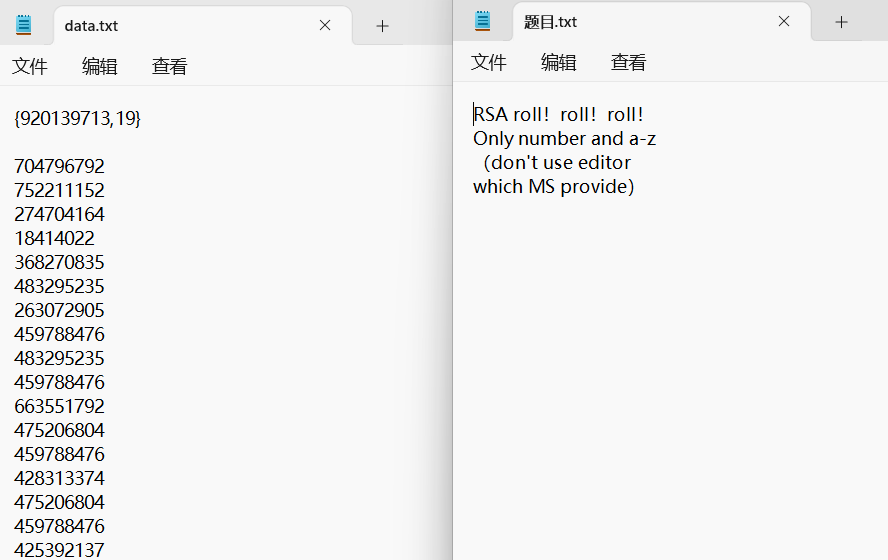
我们可以发现最前面两个数字被打上了括号，可以推测这是公钥{n,e}或是私钥{d,e}，下面的数字可能都是密文

密文应该是从明文碎片中逐个加密的，也就是说我们需要对密文逐个解密并进行拼接的到明文

我们先按照假设{n,e}是公钥的思路来编写脚本：

from Crypto.Util.number import long_to_bytes

c = [
704796792,
752211152,
274704164,
18414022,
368270835,
483295235,
263072905,
459788476,
483295235,
459788476,
663551792,
475206804,
459788476,
428313374,
475206804,
459788476,
425392137,
704796792,
458265677,
341524652,
483295235,
534149509,
425392137,
428313374,
425392137,
341524652,
458265677,
263072905,
483295235,
828509797,
341524652,
425392137,
475206804,
428313374,
483295235,
475206804,
459788476,
306220148
]
p = 18443
q = 49891
e = 19
n = 920139713
phi = (p-1)*(q-1)
d = pow(e,-1,phi)
flag = b''
for i in c:
    m = pow(i, d, n)
    flag += long_to_bytes(m)   # 将整数转换为字节并添加
print(flag.decode()) # 将字节解码为字符串并打印

得到了flag

考点：分裂的密文、理解RSA加密原理并运用n、e、c计算出m

posted @ 2024-07-17 11:51 Super_Snow_Sword 阅读(411) 评论(0) 编辑收藏举报

刷新页面返回顶部

雪剑大帅哥的豪华宫殿

【CTF入门】BUUCTF Crypto刷题（持续更新）

【CTF入门】BUUCTF Crypto刷题（持续更新）

一眼就解密

base64编码介绍

原理：https://www.bilibili.com/video/BV1hk4y1S7PJ?vd_source=69c558b0c7be97607c79afbd75bd1f7c

密文特征：

MD5

HASH算法介绍

原理：https://www.bilibili.com/video/BV1SZ4y1z7wT?vd_source=69c558b0c7be97607c79afbd75bd1f7c

密文特征：

Url编码

Url编码介绍

密文特征：

看我回旋踢

ROT13加密介绍

原理：

密文特征：

摩丝

摩斯电码介绍

原理：摩尔斯电码_百度百科 (baidu.com)

密文特征：

password

社会工程学

原理：https://www.bilibili.com/video/BV15V411u7Za?vd_source=69c558b0c7be97607c79afbd75bd1f7c

变异凯撒

Quoted-printable

Quoted-printable编码介绍

原理：

密文特征：

补充：UTF-8编码

原理：https://www.bilibili.com/video/BV1kD4y1z7ft?vd_source=69c558b0c7be97607c79afbd75bd1f7c

篱笆墙的影子

栅栏密码介绍

原理：https://www.bilibili.com/video/BV1TE41177qP?vd_source=69c558b0c7be97607c79afbd75bd1f7c

密码特征：

Rabbit

Rabbit加密介绍

RSA

RSA加密介绍

原理：https://www.bilibili.com/video/BV1XP4y1A7Ui?vd_source=69c558b0c7be97607c79afbd75bd1f7c

丢失的MD5

Alice与Bob（RSA）

大整数分解

Factordb

补充：使用工具yafu进行大整数分解

大帝的密码武器（知识巩固题）

rsarsa（RSA知识巩固题）

Windows系统密码

补充：LM哈希和NT哈希

信息化时代的步伐（新编码）

凯撒？替换？呵呵!（新密码）

不规则替换密码自动匹配的原理

萌萌哒的八戒（新密码）

猪圈密码

权限获得第一步（知识巩固题）

RSA1（新RSA）

dp是私钥d与(p-1)取余的值，即dp = d%(p-1)

同理dq = d%(q-1)

传统知识+古典密码（新孬密码）

世上无难事（知识巩固题）

Unencode（新编码）

UUencode

old-fashion（知识巩固题）

[AFCTF2018]Morse

RSA3（新RSA）

共模攻击

RSA2

dp泄露

还原大师（知识巩固题）

异性相吸（新加密脑洞）

异或加密

RSA（新RSA）

PEM格式

公钥解析原理

1. 读取公钥文件

2. Base64 解码

3. ASN.1 解码

4. 提取参数

RSAROLL