查并集

1.引入

查并集：查并集是什么？上来先不讲概念，先用例子引入，老师好像是这样讲课的。

猫猫集合：小王和小刘是亲戚，小张和小刘是亲戚
狗子集合：小赵和小云是亲戚
那么小动物的亲戚圈如下，请问小赵和小王是亲戚吗？

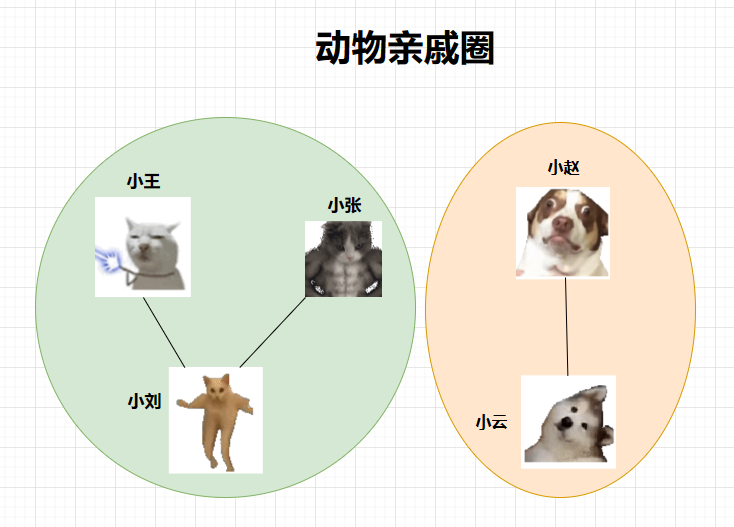
将以上语言,转换为程序语言：

输入（A,B）(C,B) (D,E)
请问有几个亲戚圈？
亲戚最大有多少？
A、C是不是亲戚？

当然，圈子这个词也该换换了

输入（A,B）(C,B) (D,E) 无向路径
请问有几个连通分量？
最大连通分量是多少？
A、C是不是可连通的？

查并集

我们怎么知道小王、小张、小刘是一个圈子的人？喔， 把你的心我的心串一串，串一株幸运草串一个同心圆， 让所有期待未来的呼唤。
没错就是串一串，假如果我们这么串：

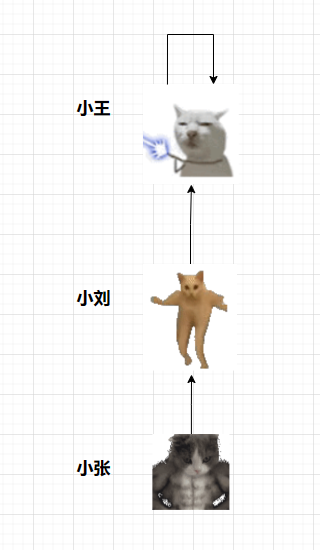
小刘的Root是小王、小张的Root是小网、小王的Root是小王。他们的Root相同，我们说他们是一个圈子的人，是亲戚。

那么问题来了？怎么构建这个树，哦不，串。

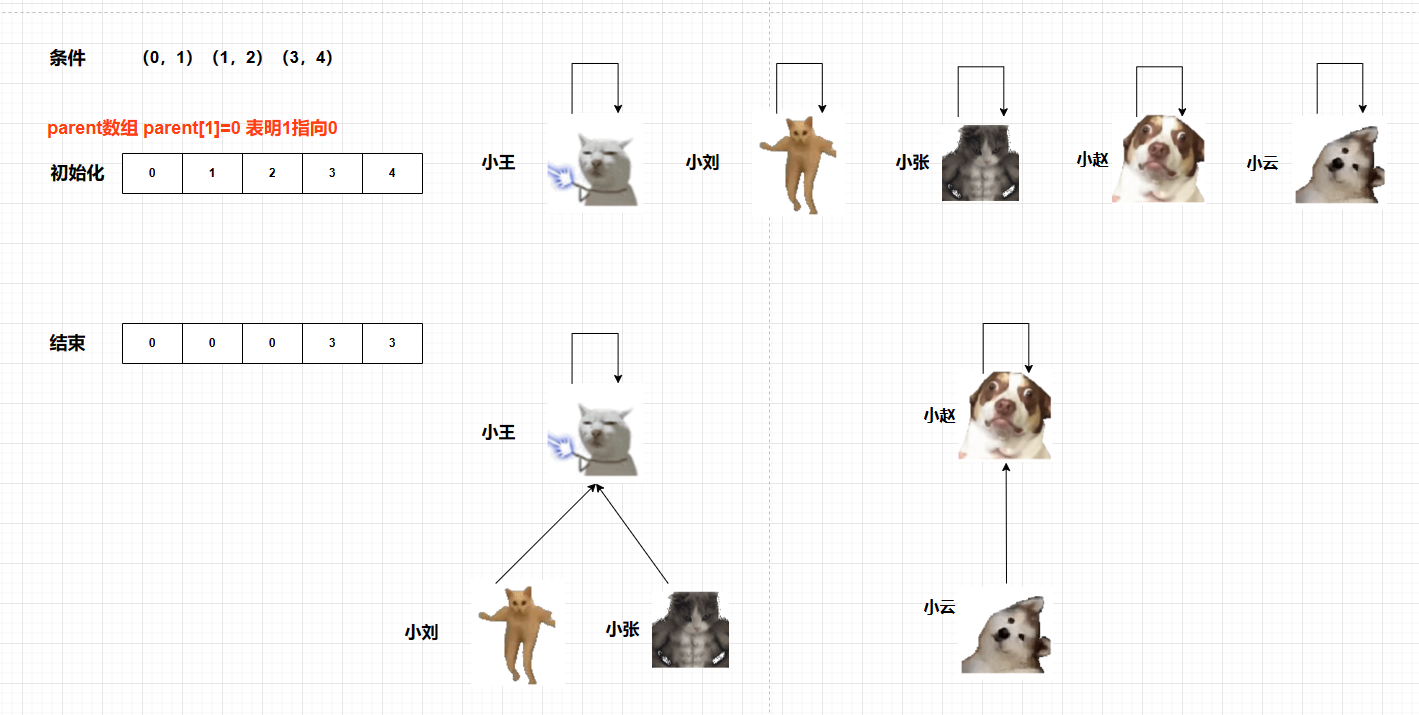
哦哦哦，太神奇了，现在我想问的是，数组怎么转换来的？
那不得不讲三个方法：

// parent数组 parent[1]=0 表明1指向0
int[] parent=new int[];

1. MAKE-SET:创建一个新的集合，初始化每个元素都是一个集合,每个元素的parent都是自己。

for(int i=0;i<5;i++){
    parent[i]=i;
}

2. FIND-SET(x):寻找一个SET的代表元素，也就是根元素

int find(int x){
    if(x!=parent[x]){ //你的指针不指向你
        x=find(parent[x]);
    }
    return x;
}

3. UNION(x,y):将x，y两个集合合并

void union(int x,int y){
    int x=find(x);
    int y=find(y);
    if(x!=y){
        parent[x]=y;
    }
}

哦,那程序怎么写？

class Union-Find{
    int[] parent;
    public Union(int x){
        parent=new int[x];
        for(int i=0;i<x;i++){
            parent[i]=i;
        }
    }

    int find(int x){
        if(x!=parent[x]){ //你的指针不指向你
            x=find(parent[x]);
        }
        return x;
    }
    void union(int x,int y){
        int x=find(x);
        int y=find(y);
        if(x!=y){
            parent[x]=y;
    }
    boolean isConnect(x,y){
        return find(x)==find(y);
    }
}

public class Main{
    public static void  main(string[] args){
        UnionFind unionFind=new UnionFind(5);
        unionFind.union(0,1);
        unionFind.union(1,2);
        unionFind.union(3,4);
        System.out.println(unionFind.isConnect(1,4));
    }
}

哦，天下无敌了，那做个题试试。🐔🐔🐔漏出鸡脚。

查并集题目练习

朋友圈(后端开发卷)
现在有 105 个用户，编号为 1- 105，现在已知有 m 对关系，每一对关系给你两个数 x 和 y ，代表编号为 x 的用户和编号为 y 的用户是在一个圈子中，例如： A 和 B 在一个圈子中， B 和 C 在一个圈子中，那么 A , B , C 就在一个圈子中。现在想知道最多的一个圈子内有多少个用户。

输入描述：

第一行输入一个整数T，接下来有T组测试数据。
对于每一组测试数据：第一行输入1个整数n，代表有n对关系。
接下来n行，每一行输入两个数x和y，代表编号为x和编号为y的用户在同一个圈子里。
1 ≤ T ≤ 10
1 ≤ n ≤ 2*106
1 ≤ x, y ≤ 105

输出描述：

对于每组数据，输出一个答案代表一个圈子内的最多人数

示例1
输入例子：

2
4
1 2
3 4
5 6
1 6
4
1 2
3 4
5 6
7 8

输出例子：

4
2

代码:

class UnionNode {

    Integer parent;
    Integer size;

    public UnionNode(Integer parent, Integer size) {
        this.parent = parent;
        this.size = size;
    }

    public Integer getParent() {
        return parent;
    }

    public void setParent(Integer parent) {
        this.parent = parent;
    }

    public Integer getSize() {
        return size;
    }

    public void setSize(Integer size) {
        this.size = size;
    }
}

class UnionFind {
    /**
     * parent[i]表示i这个元素指向的父亲节点
     */
    HashMap<Integer, UnionNode> parent;
    int setCount;

    public UnionFind() {
        parent = new HashMap<>();

    }

    int getMaxSize() {
        int max = 0;
        for (Map.Entry<Integer, UnionNode> entry : parent.entrySet()) {
            max = max > entry.getValue().getSize() ? max : entry.getValue().getSize();
        }
        return max;
    }

    public int find(int x) {
        if (!parent.containsKey(x)) {
            parent.put(x, new UnionNode(x, 1));
            setCount++;
        }
        return parent.get(x).getParent() == x ? x : find(parent.get(x).getParent());
    }

    public boolean unit(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) {
            return false;
        }
        if (parent.get(x).getSize() < parent.get(y).getSize()) {
            int tem = x;
            x = y;
            y = tem;
        }
        int xsize = parent.get(x).getSize();
        int ysize = parent.get(y).getSize();
        parent.put(y, new UnionNode(x, 0));
        parent.get(x).setSize(xsize + ysize);
        --setCount;
        return true;
    }

    public boolean connected(int x, int y) {
        x = find(x);
        y = find(y);
        return x == y;
    }

}

public class DemoApplication {
    public static void main(String[] args) {
        UnionFind unionFind = new UnionFind();
        unionFind.unit(0, 1);
        unionFind.unit(1, 2);
        unionFind.unit(3, 4);
        System.out.println(unionFind.getMaxSize());
    }
}