二分查找法

1. 描述

要求：

1. 数组 2. 有序

2. 代码

class Solution {
    public int search(int[] nums, int target) {
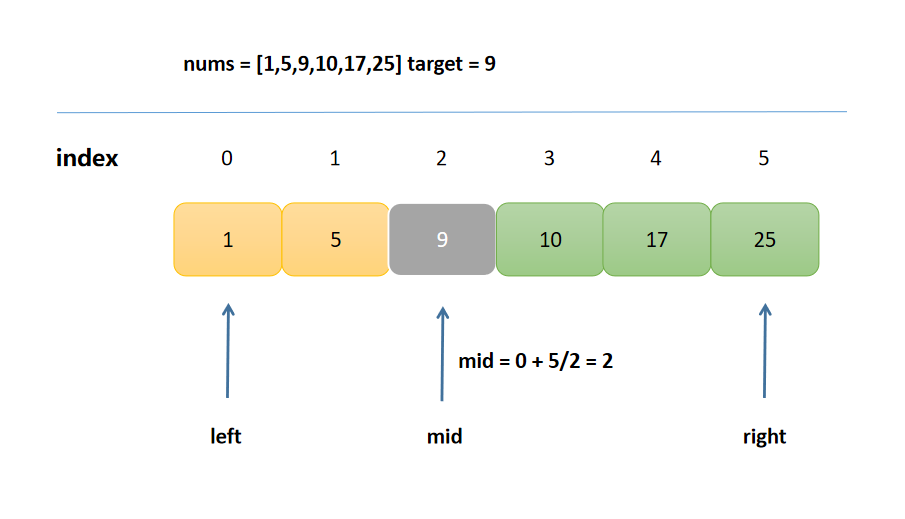
        int left = 0;
        int right = nums.length - 1;
        while (left <= right) { //nums=[1] target=1 => left=0 right=0
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return -1;
    }
}

3. 时间、空间复杂度

时间复杂度：O(logn)
空间复杂度：O(1)

4. 附录

4.1 查找左边第一个元素

nums = [5,7,7,8,8,10], target = 7
result = 1

    int findLeftLocation(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1; // 初始化 right 为最后一个有效索引
        while (left <= right) { // 循环条件改为 left 小于等于 right
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                right = mid - 1; // 移动 right 到 mid - 1 以找到最左边的 target
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }

        // 检查 left 是否在数组范围内且 nums[left] 是否等于 target
        if (left >= nums.length || nums[left] != target) {
            return -1;
        }
        return left;
    }

4.1 查找右边第一个元素

nums = [5,7,7,8,8,10], target = 7
result = 2

    int findRightLocation(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1; // 初始化 right 为最后一个有效索引
        while (left <= right) { // 循环条件改为 left 小于等于 right
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                left = mid + 1; // 移动 left 到 mid + 1 以找到最右边的 target
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }

        // 检查 right 是否在数组范围内且 nums[right] 是否等于 target
        if (right < 0 || nums[right] != target) {
            return -1;
        }
        return right;
    }