uva-699 Not so Mobile (杠杆,巧妙递归)
| Not so Mobile |
Before being an ubiquous communications gadget, a mobile was just a structure made of strings and wires suspending colourfull things. This kind of mobile is usually found hanging over cradles of small babies.
The figure illustrates a simple mobile. It is just a wire, suspended by a string, with an object on each side. It can also be seen as a kind of lever with the fulcrum on the point where the string ties the wire. From the lever principle we know that to balance a simple mobile the product of the weight of the objects by their distance to the fulcrum must be equal. That isWl×Dl = Wr×Dr where Dl is the left distance, Dr is the right distance, Wl is the left weight and Wr is the right weight.
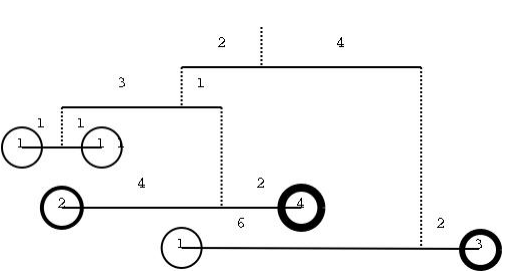
In a more complex mobile the object may be replaced by a sub-mobile, as shown in the next figure. In this case it is not so straightforward to check if the mobile is balanced so we need you to write a program that, given a description of a mobile as input, checks whether the mobile is in equilibrium or not.

Input
The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs.
The input is composed of several lines, each containing 4 integers separated by a single space. The 4 integers represent the distances of each object to the fulcrum and their weights, in the format: Wl Dl Wr Dr
If Wl or Wr is zero then there is a sub-mobile hanging from that end and the following lines define the the sub-mobile. In this case we compute the weight of the sub-mobile as the sum of weights of all its objects, disregarding the weight of the wires and strings. If both Wl and Wr are zero then the following lines define two sub-mobiles: first the left then the right one.
Output
For each test case, the output must follow the description below. The outputs of two consecutive cases will be separated by a blank line.
Write `YES' if the mobile is in equilibrium, write `NO' otherwise.
Sample Input
1 0 2 0 4 0 3 0 1 1 1 1 1 2 4 4 2 1 6 3 2
Sample Output
YES
题解:题意是让求这个杠杆是不是平衡;看了大神的代码,处理的很巧妙,如果当前质量是0,递归输入子天平,每个子天平判断是否平衡,就可以了;
代码:
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
#define SI(x) scanf("%d",&x)
#define mem(x,y) memset(x,y,sizeof(x))
#define PI(x) printf("%d",x)
#define P_ printf(" ")
const int INF=0x3f3f3f3f;
typedef long long LL;
bool solve(int &w){
int w1,d1,w2,d2;
scanf("%d%d%d%d",&w1,&d1,&w2,&d2);
int temp1=true,temp2=true;
if(!w1)temp1=solve(w1);
if(!w2)temp2=solve(w2);
w=w1+w2;
if(w1*d1==w2*d2&&temp1&&temp2)return true;
else return false;
}
int main(){
int T;
SI(T);
while(T--){
int w;
if(solve(w))puts("YES");
else puts("NO");
if(T)puts("");
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号