求树的直径（两种方法）
① 两次dfs
方法：先从任意一点P出发，找离它最远的点Q，再从点Q出发，找离它最远的点W，W到Q的距离就是是的直径
证明如下：
①若P已经在直径上，根据树的直径的定义可知Q也在直径上且为直径的一个端点
②若P不在直径上，我们用反证法，假设此时WQ不是直径，AB是直径
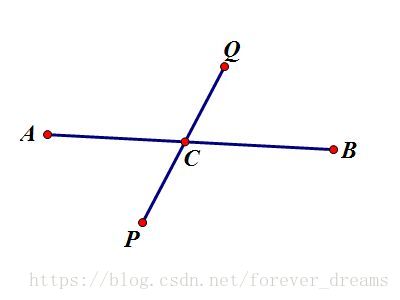
--->若AB与PQ有交点C，由于P到Q最远，那么PC+CQ>PC+CA，所以CQ>CA，易得CQ+CB>CA+CB，即CQ+CB>AB，与AB是直径矛盾，不成立，如下图（其中AB，PQ不一定是
直线，画成直线是为了方便）：
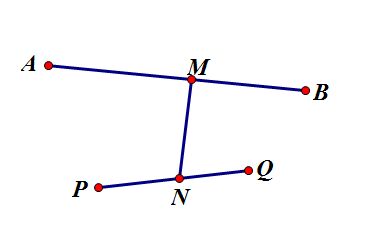
--->若AB与PQ没有交点，M为AB上任意一点，N为PQ上任意一点。首先还是NP+NQ>NQ+MN+MB，同时减掉NQ，得NP>MN+MB，易知NP+MN>MB，所NP+MN+MA>MB+MA，
即NP+MN+MA>AB，与AB是直径矛盾，所以这种情况也不成立，如下图：
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define maxn 100000 6 using namespace std; 7 inline int read() 8 { 9 int x=0; 10 bool f=1; 11 char c=getchar(); 12 for(; !isdigit(c); c=getchar()) if(c=='-') f=0; 13 for(; isdigit(c); c=getchar()) x=(x<<3)+(x<<1)+c-'0'; 14 if(f) return x; 15 return 0-x; 16 } 17 struct node 18 { 19 int u,v,w,nex; 20 }edge[2*maxn+10]; 21 int n,m,d[maxn+10],head[maxn+10],f_num,cnt=0,ans; 22 inline void add(int x,int y,int z) 23 { 24 cnt++; 25 edge[cnt].u=x; 26 edge[cnt].v=y; 27 edge[cnt].w=z; 28 edge[cnt].nex=head[x]; 29 head[x]=cnt; 30 } 31 inline void dfs(int x,int fa) 32 { 33 if(ans<d[x]) 34 { 35 ans=d[x]; 36 f_num=x; 37 } 38 for(int i=head[x];i!=-1;i=edge[i].nex) 39 { 40 int j=edge[i].v; 41 if(j==fa)continue; 42 d[j]=d[x]+edge[i].w; 43 dfs(j,x); 44 } 45 } 46 int main() 47 { 48 memset(head,-1,sizeof(head)); 49 n=read();m=read(); 50 for(int i=1;i<=m;i++) 51 { 52 int x,y,z; 53 x=read();y=read();z=read(); 54 add(x,y,z); 55 add(y,x,z); 56 } 57 dfs(1,0); 58 ans=0; 59 d[f_num]=0; 60 dfs(f_num,0); 61 printf("%d",ans); 62 return 0; 63 }
② 树形DP
对于每个节点我们要记录两个值：f1 [ i ] 表示以 i 为根的子树中，i 到叶子结点距离的最大值f2 [ i ] 表示以 i 为根的子树中，i 到叶子结点距离的次大值对于一个节点，它到叶子结点距
离的最大值和次大致所经 过的路径肯定是不一样的若j是i的儿子，那么（下面的 w [ i ][ j ] 表示 i 到 j 的路径长度）：
若 f1 [ i ] < f1 [ j ] + w [ i ][ j ]，f2 [ i ] =f1 [ i ]，f1 [ i ] = f1 [ j ] + w [ i ][ j ]；
否则，若 f2 [ i ] < f1 [ j ] + w [ i ][ j ]，f2 [i ] = f1 [ j ] + w [ i ][ j ]；
理解：这样做就是，先看能否更新最大值，若能，它的次大值就是原先的最大值，再更新它的最大值；若不能，就看能不能更新次大值，若能，就更新，不能就不管它
这样的话，最后的答案 answer = max { f1 [ i ] + f2[ i ] }
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define maxn 100000 6 #define INF 2147483647/2-1 7 using namespace std; 8 inline int read() 9 { 10 int x=0; 11 bool f=1; 12 char c=getchar(); 13 for(; !isdigit(c); c=getchar()) if(c=='-') f=0; 14 for(; isdigit(c); c=getchar()) x=(x<<3)+(x<<1)+c-'0'; 15 if(f) return x; 16 return 0-x; 17 } 18 int n,m,ans,f1[maxn+10],f2[maxn+10],head[maxn+10],cnt=0; 19 struct node 20 { 21 int u,v,w,nex; 22 }edge[2*maxn+10]; 23 inline void add(int x,int y,int z) 24 { 25 cnt++; 26 edge[cnt].u=x; 27 edge[cnt].v=y; 28 edge[cnt].w=z; 29 edge[cnt].nex=head[x]; 30 head[x]=cnt; 31 } 32 inline void dp(int x,int fa) 33 { 34 for(int i=head[x];i!=-1;i=edge[i].nex) 35 { 36 int j=edge[i].v; 37 if(j==fa)continue; 38 dp(j,x); 39 if(f1[x]<f1[j]+edge[i].w) 40 { 41 f2[x]=f1[x]; 42 f1[x]=f1[j]+edge[i].w; 43 } 44 else if(f2[x]<f1[j]+edge[i].w) 45 { 46 f2[x]=f1[j]+edge[i].w; 47 } 48 ans=max(ans,f1[x]+f2[x]); 49 } 50 } 51 int main() 52 { 53 memset(head,-1,sizeof(head)); 54 n=read();m=read(); 55 for(int i=1;i<=m;i++) 56 { 57 int x,y,z; 58 x=read();y=read();z=read(); 59 add(x,y,z); 60 add(y,x,z); 61 } 62 dp(1,0); 63 printf("%d",ans); 64 return 0; 65 }
原文作者：forever_dreams 来源：CSDN
请各位大佬斧正（反正我不认识斧正是什么意思）
