min-max容斥

前置芝士：

二项式反演：

$f_n=\sum\limits_{i=0}^{n} (-1)^{i} \times C_{n}^{i} g_i \Leftrightarrow g_n=\sum\limits_{i=0}^{n} (-1)^{i} \times C_{n}^{i} f_i$

$f_n=\sum\limits_{i=0}^{n} C_{n}^{i} g_i \Leftrightarrow g_n=\sum\limits_{i=0}^{n} (-1)^{n-i} \times C_{n}^{i} f_i$

$f_n=\sum\limits_{i=k}^{n} C_{n}^{i} g_i \Leftrightarrow g_n=\sum\limits_{i=k}^{n} (-1)^{i-k} \times C_{n}^{i} f_i$

设$max(S)$表示集合S中的最大元素，$min(S)$表示集合S中的最小元素，$|S|$表示集合S中的元素个数

结论1：$max(S)=\sum\limits_{T \subset S} (-1)^{|T|+1} min(T)$

$min(S)=\sum\limits_{T \subset S} (-1)^{|T|+1} max(T)$

证明：

我们考虑构造容斥系数$f(x)$

使得$max(S)=\sum\limits_{T \subset S} f(|T|+1) min(T)$成立

对于从小到大的第x项，在右式计算次数为：$\sum\limits_{i=0}^{n-x} C_{n-x}^{i}*f(i+1)$

即有$[x==n]=\sum\limits_{i=0}^{n-x} C_{n-x}^{i}*f(i+1)$

$[n-x==0]=\sum\limits_{i=0}^{n-x} C_{n-x}^{i}*f(i+1)$

$[x==0]=\sum\limits_{i=0}^{x} C_{x}^{i}*f(i+1)$

二项式反演得：$f(x+1)=\sum\limits_{i=0}^{x} (-1)^{x-i} \times C_{x}^{i}*[i==0]$

$\therefore f(x+1)=(-1)^{x}$

$\therefore f(x)=(-1)^{x+1}$

证毕

结论2：结论1在期望的条件下也成立，即

 

$E（max(S)）=\sum\limits_{T \subset S} (-1)^{|T|+1} E(min(T))$

 

$E(min(S))=\sum\limits_{T \subset S} (-1)^{|T|+1} E(max(T))$

 

进阶：$kthmax(S)=\sum\limits_{T \subset S} (-1)^{|T|-k}  \times C_{|T|-1}^{k-1} min(T)$

求第k大的数的表达式

我们考虑构造容斥系数$f(x)$

使得$kthmax(S)=\sum\limits_{T \subset S} f(|T|+1) min(T)$成立

即有$[x==n-k+1]=\sum\limits_{i=0}^{n-x} C_{n-x}^{i}*f(i+1)$

$[n-k-x+1==0]=\sum\limits_{i=0}^{n-x} C_{n-x}^{i}*f(i+1)$

$[x==k-1]=\sum\limits_{i=0}^{x} C_{n-x}^{i}*f(i+1)$

二项式反演得：$f(x+1)=\sum\limits_{i=0}^{x} (-1)^{x-i} \times C_{x}^{i}*[i==k-1]$

$f(x+1)=\sum\limits_{i=0}^{x} (-1)^{x-i} \times C_{x}^{i}*[i==k-1]$

$f(x+1)=(-1)^{x-k+1} \times C_{x}^{k-1}$

$f(x)=(-1)^{x-k} \times C_{x-1}^{k-1}$

证毕

 例题1：按位或

 

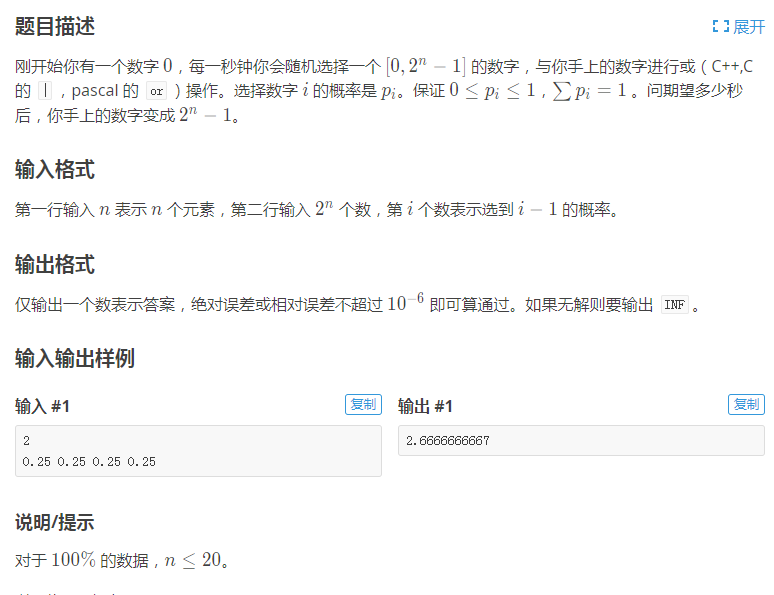
并不容易想到要用min-max容斥

设E(max(S))表示S这个二进制数中最后一个1的出现时间

而E(min(S))表示S这个二进制数中第一个1的出现时间

则有$E（max(S)）=\sum\limits_{T \subset S} (-1)^{|T|+1} E(min(T))$

且容易想到$E(min(S))=\frac{1}{\sum\limits_{T \cap S \neq \emptyset} p(T)}$

那么现在问题就变成了如何求$T \cap S$

正难则反，考虑求$T \cup S=\emptyset$

发现这正好是S的补集的子集和

然后就做完了趴qwq