Helping People

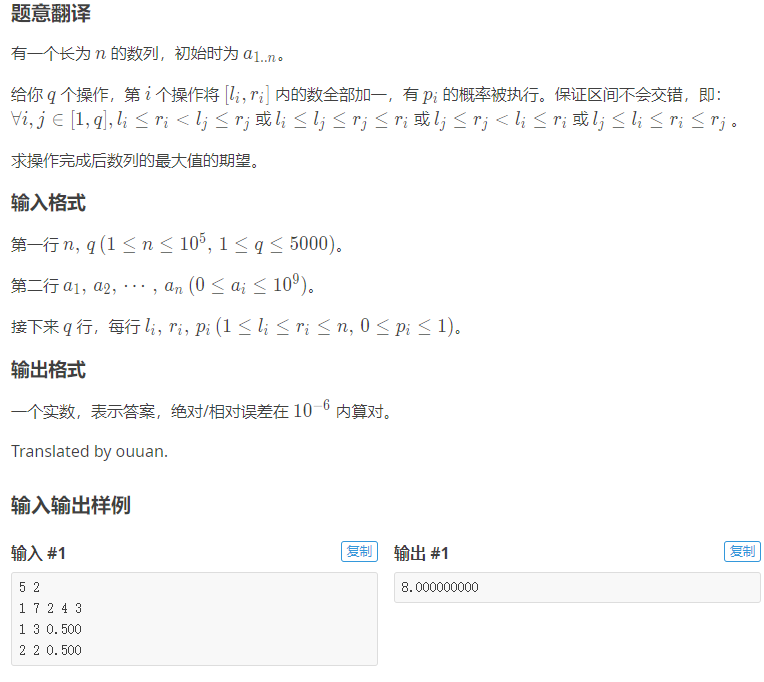
由于操作的区间互不重叠，所以我们将区间以相互包含的关系建树

$n^2$树状dp，设$dp[i][j]$表示第i个区间最大值小于等于$max(a[l[i]],…,a[r[i]])+j$的概率

设d[i]为$max(a[l[i]],…,a[r[i]])$

转移还是比较好推的：$dp[i][j]=p_i\prod\limits_{v是i的儿子} dp[i][d[i]-d[v]+j-1] \space+ \space (1-p_i)\prod\limits_{v是i的儿子} dp[i][d[i]-d[v]+j]$

#include<bits/stdc++.h>
#define maxn 100005
#define maxm 500005
#define inf 0x7fffffff
#define ll long long
#define rint register int
#define debug(x) cerr<<#x<<": "<<x<<endl
#define fgx cerr<<"--------------"<<endl
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define dgx cerr<<"=============="<<endl
#define lowbit(x) (x&(-x))
#define MAXN 5005
using namespace std;
inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while('0'>ch || ch>'9'){if(ch=='-') f=-1; ch=getchar();}
	while('0'<=ch && ch<='9'){x=(x<<1)+(x<<3)+ch-'0'; ch=getchar();}
	return x*f;
}
int n,m,b[maxn],d[MAXN],book[MAXN];
double ans,dp[MAXN][MAXN];
struct node{
	int l,r;
	double x;
}a[MAXN];
bool cmpp(node a1,node a2){
	return a1.r-a1.l<a2.r-a2.l;
}
struct Segment_Tree{
	int c[maxn<<2];
	void build(int k,int l,int r){
		if(l==r){c[k]=b[l]; return;}
		int mid=(l+r)>>1;
		build(k<<1,l,mid); build((k<<1)|1,mid+1,r);
		c[k]=max(c[k<<1],c[k<<1|1]);
	}
	int query(int k,int l,int r,int x,int y){
		if(x<=l && r<=y) return c[k];
		int maxx=-1,mid=(l+r)>>1;
		if(mid>=x) maxx=query(k<<1,l,mid,x,y);
		if(mid<y) maxx=max(maxx,query((k<<1)|1,mid+1,r,x,y));
		return maxx;
	}
}Q;
int to[maxn],fir[maxn],nxt[maxn],tot;
void ade(int x,int y){
	to[++tot]=y;
	nxt[tot]=fir[x];
	fir[x]=tot;
}
void work(int x){
	dp[x][0]=1-a[x].x;
	d[x]=Q.query(1,1,n,a[x].l,a[x].r);
	rep(i,1,x-1) if(a[x].l<=a[i].l && a[i].r<=a[x].r && !book[i]){ if(d[x]-d[i]<=m) dp[x][0]*=dp[i][d[x]-d[i]]; ade(x,i);}
	rep(j,1,m+1){
		double z1=1,z2=1;
		for(int i=fir[x];i;i=nxt[i]) if(d[x]-d[to[i]]-1+j<=m) z1=z1*dp[to[i]][d[x]-d[to[i]]-1+j],z2=z2*dp[to[i]][d[x]-d[to[i]]+j];
		dp[x][j]=z1*a[x].x+z2*(1-a[x].x);
	}
	rep(i,1,x-1) if(a[x].l<=a[i].l && a[i].r<=a[x].r && !book[i]) book[i]=1;
}
int main(){
    scanf("%d%d",&n,&m);
    rep(i,1,n) b[i]=read();
    rep(i,1,m){
    	a[i].l=read(); a[i].r=read();
    	scanf("%lf",&a[i].x);
	}
	m++;Q.build(1,1,n);
	a[m].l=1; a[m].r=n; a[m].x=0;
	sort(a+1,a+m+1,cmpp);
	rep(i,1,m) work(i);ans=d[m]*dp[m][0];
	rep(i,1,m) ans=ans+(d[m]+i)*(dp[m][i]-dp[m][i-1]);
	printf("%.10lf",ans);
	return 0;
}