奖牌分配/Median Pyramid Hard

题目背景

有一个环形的围墙，围墙上有一些塔，每个塔中有一个守卫。

题目描述

现在要发给每个守卫一些奖章，第i个守卫需要P[i]个奖章。每个守卫自己的奖章必须都是不同种类的，而且相邻的两个守卫得到的奖章也不能有任何一个相同。问至少应准备多少种不同的奖章。（限制：2≤n≤10000，1≤P[i]≤100000）

输入格式

1个n，n个数pi

输出格式

一个数

输入输出样例

输入 

  4

1 1 2 2

输出 

4

二分答案，设x为mid-p[1]，可涉DP[i][j]表示第i个守卫有j个奖牌与第1个相同，列出DP方程：

    $dp[i][j]=\sum\limits_{k=0}^{j} dp[i][j] | dp[i][k]$

我们发现，如果第i个守卫最少可以有x个、最多可以有y个奖牌与1号相同，那么在[x,y]区间内一定都可以满足此时的要求(用k的范围可知)，所以只需记录该区间的左右端点即可
注意二分答案的左端点应为相邻两个守卫需求的和的最大值
CODE：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define rep(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
int n,a[100005],x[100005],y[100005],l,r;
bool check(int t){
    x[1]=y[1]=a[1];
    rep(i,2,n){
        x[i]=max(0,a[1]+a[i-1]+a[i]-y[i-1]-t);
        y[i]=min(a[i],a[1]-x[i-1]);
        if(x[i]>y[i]) return 0;
    }
    if(!x[n]) return 1;
    else return 0;
}
int main(){
    scanf("%d",&n);
    rep(i,1,n){
        scanf("%d",&a[i]);
        l=max(a[i]+a[i-1],l);
    }
    l=max(l,a[1]+a[n]);
    r=300001;
    while(l<r){
        int mid=(l+r)>>1;;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    cout<<l;
}

Median Pyramid Hard：
【问题描述】 你有一个底部宽为 2N-1 的金字塔，除了底层以外，每一个位置的数都是下面三个数的 中位数。求塔顶的数是多少？ 
 
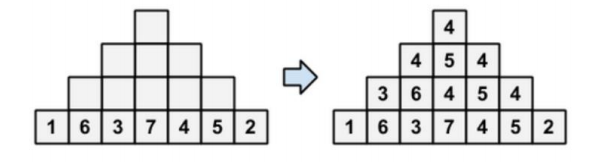
【输入格式】 第一行包含一个整数：N 第二行 2N-1 个正整数，依次表示数字三角形最底下一层的数字 
【输出格式】 一行包含一个整数 x，表示所求的答案 
【输入样例】 4 1 6 3 7 4 5 2 
【输出样例】 4
【数据规模】
  40 分 1≤n≤2000 
  60 分 1≤n≤100000

很容易想出来的模拟，发现它无法再优化了

我们想一想能不能通过其他奇奇怪怪的算法将复杂度里面的一个n优化成log

想到二分答案，能否将数字串转化成一个01串来解决问题

二分答案，然后将小于该值的数设为0，反之设为1

我们发现只要是一个长度大于1的连续串每次上调都不变（除左右两边每次减1），只有零零散散的串（such as 0101）才会不断改变

然后我们分类讨论下即可，代码还是非常好写的

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define rep(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
int n,a[2000500],b[2000005],r,l;
void work(int x,int y){
    if((y-x)&1){
        if(n>=(y-x+1)/2){
            rep(i,x,(y+x)/2) b[i]=b[x];
            rep(i,(y+x)/2+1,y) b[i]=b[y];
        }
        else{
            rep(i,x,x+n-1) b[i]=b[x];
            rep(i,x+n,y-n) if((i-x-n)%2==0) b[i]=b[x]; else b[i]=b[y];
            rep(i,y-n+1,y) b[i]=b[y];
        }
    }
    else{
        rep(i,x,y) b[i]=b[x];
        if(n<=(y-x)/2) rep(i,x+n,y-n) if((i-x-n)%2==0) b[i]=1-b[x];else b[i]=b[x];
    }
}
bool check(int x){
    rep(i,1,2*n-1) if(a[i]>=x) b[i]=1;else b[i]=0;
    b[2*n]=2;
    int st=-1;
    rep(i,1,2*n-1){
        if(st!=-1 && b[i]==b[i+1]) work(st,i),st=-1;
        if(st==-1 && b[i]!=b[i+1]) st=i;
    }
    if(st!=-1) work(st,2*n-1);
    return b[n];
}
int main(){
    scanf("%d",&n);
    rep(i,1,2*n-1) scanf("%d",&a[i]),r=max(r,a[i]);
    l=1;
    while(l<r){
        int mid=(l+r+1)>>1;
        if(check(mid)) l=mid;
        else r=mid-1;
    }
    printf("%d",l);
    return 0;
}