树链剖分
树链剖分
其实我是来push一篇dalao文章:https://www.cnblogs.com/ivanovcraft/p/9019090.html
这个东西其实就是用玄学奇奇怪怪的方法来优化暴力,把树分成重链和轻链,然后重链是一条链,dfs序相连,可以用线段树这样的数据结构来优化,轻链暴力即可,可以轻松证明,一条树上的路径最多有log(n)条轻链+重链,所以树链剖分每次的时间复杂度就是O(nlog^2n)
好的
看一些例题
1.P3384 【模板】树链剖分
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
输入输出样例
说明
时空限制:1s,128M
数据规模:
对于30%的数据: N \leq 10, M \leq 10N≤10,M≤10
对于70%的数据: N \leq {10}^3, M \leq {10}^3N≤103,M≤103
对于100%的数据: N \leq {10}^5, M \leq {10}^5N≤105,M≤105
( 其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233 )
样例说明:
树的结构如下:

各个操作如下:

故输出应依次为2、21(重要的事情说三遍:记得取模)
简简单单的板子,上代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define rep(i,a,b) for(long long i=a;i<=b;i++)
#define MAXN 100050
using namespace std;
typedef long long ll;
ll n,m,r,mod;
ll fa[MAXN],son[MAXN],to[MAXN<<1],nxt[MAXN<<1],fir[MAXN],tot,cnt;
ll seg[MAXN],rk[MAXN],dep[MAXN],siz[MAXN],top[MAXN],w[MAXN];
void dfs1(ll x,ll f){
// cout<<x<<"h h"<<f<<endl;
dep[x]=dep[f]+1;
fa[x]=f;
siz[x]=1;
for(ll k=fir[x];k;k=nxt[k]){
if(to[k]!=f){
dfs1(to[k],x);
siz[x]+=siz[to[k]];
if(siz[son[x]]<siz[to[k]]) son[x]=to[k];
}
}
}
void ade(ll u,ll v){
to[++tot]=v;
nxt[tot]=fir[u];
fir[u]=tot;
}
void dfs2(ll x,ll y){
// cout<<x<<"h h"<<y<<endl;
seg[x]=++cnt;
rk[cnt]=x;
top[x]=y;
if(!son[x]) return;
dfs2(son[x],y);
for(ll k=fir[x];k;k=nxt[k]) if(to[k]!=fa[x] && to[k]!=son[x]) dfs2(to[k],to[k]);
}
struct zlk{
ll sum[400050],add[400050];
void pre(ll k,ll l,ll r){
add[k]=0;
if(l==r){sum[k]=w[rk[l]]; return;}
ll mid=(l+r)>>1;
pre(k<<1,l,mid); pre((k<<1)|1,mid+1,r);
sum[k]=sum[k<<1]+sum[(k<<1)|1];
}
void work(ll k,ll l,ll r,ll v){
add[k]+=v; add[k]%=mod;
sum[k]+=v*(r-l+1); sum[k]%=mod;
}
void push_down(ll k,ll l,ll r,ll mid){
if(!add[k]) return;
work(k<<1,l,mid,add[k]); work((k<<1)|1,mid+1,r,add[k]);
add[k]=0;
}
void adds(ll k,ll l,ll r,ll x,ll y,ll z){
if(x<=l && r<=y){
work(k,l,r,z);
return;
}
if(l==r) return;
ll mid=(l+r)>>1;
push_down(k,l,r,mid);
if(mid>=x) adds(k<<1,l,mid,x,y,z);
if(mid<y) adds((k<<1)|1,mid+1,r,x,y,z);
sum[k]=sum[k<<1]+sum[(k<<1)|1];sum[k]%=mod;
}
ll find(ll k,ll l,ll r,ll x,ll y){
if(x<=l && r<=y) return sum[k];
if(l==r) return 0;
ll mid=(l+r)>>1,s=0;
push_down(k,l,r,mid);
if(mid>=x) s+=find(k<<1,l,mid,x,y);
if(mid<y) s+=find((k<<1)|1,mid+1,r,x,y);
s%=mod;
return s;
}
}Q;
void work2(ll x,ll y){
ll ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans+=Q.find(1,1,n,seg[top[x]],seg[x]); x=fa[top[x]];
ans%=mod;
}
if(dep[x]<dep[y]) swap(x,y);
ans+=Q.find(1,1,n,seg[y],seg[x]);
printf("%lld\n",ans%mod);
}
void work1(ll x,ll y,ll z){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
Q.adds(1,1,n,seg[top[x]],seg[x],z); x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
Q.adds(1,1,n,seg[y],seg[x],z);
}
int main(){
scanf("%lld%lld%lld%lld",&n,&m,&r,&mod);
rep(i,1,n) scanf("%lld",&w[i]);
rep(i,1,n-1){
ll a,b; scanf("%lld%lld",&a,&b);
ade(a,b); ade(b,a);
}
dfs1(r,0);
dfs2(r,r);
//rep(i,1,n) printf("%d %d %d %d\n",son[i],fa[i],seg[i],rk[i]);
Q.pre(1,1,n);
rep(i,1,m){
ll a,b,c,d;
scanf("%lld%lld",&a,&b);
if(a==4){
printf("%lld\n",Q.find(1,1,n,seg[b],seg[b]+siz[b]-1)%mod);
continue;
}
scanf("%lld",&c);
if(a==3) Q.adds(1,1,n,seg[b],seg[b]+siz[b]-1,c);
else if(a==2) work2(b,c);
else{
scanf("%lld",&d);
work1(b,c,d);
}
}
return 0;
}
2.LOJ139树链剖分
试题描述
这是一道模板题。
给定一棵 n 个节点的树,初始时该树的根为 1 号节点,每个节点有一个给定的权值。下面依次进行 m个操作,操作分为如下五种类型:
1.换根:将一个指定的节点设置为树的新根。
2.修改路径权值:给定两个节点,将这两个节点间路径上的所有节点权值(含这两个节点)增加一个给定的值。
3.修改子树权值:给定一个节点,将以该节点为根的子树内的所有节点权值增加一个给定的值。
4.询问路径:询问某条路径上节点的权值和。
5.询问子树:询问某个子树内节点的权值和。
输入
第一行为一个整数 n,表示节点的个数。
第二行 n 个整数表示第 i 个节点的初始权值 ai。
第三行 n−1 个整数,表示i+1 号节点的父节点编号 fi+1 (1<=fi+1<=n)。
第四行一个整数 m,表示操作个数。
接下来 m 行,每行第一个整数表示操作类型编号: (1<=u,v<=n)
• 若类型为 1,则接下来一个整数 u,表示新根的编号。
• 若类型为 2,则接下来三个整数u,v,k,分别表示路径两端的节点编号以及增加的权值。
• 若类型为 3,则接下来两个整数 u,k,分别表示子树根节点编号以及增加的权值。
• 若类型为 4,则接下来两个整数 u,v,表示路径两端的节点编号。
• 若类型为 5,则接下来一个整数 u,表示子树根节点编号。
输出
对于每一个类型为 4 或5 的操作,输出一行一个整数表示答案。
输入示例
样例输入
6
1 2 3 4 5 6
1 2 1 4 4
6
4 5 6
2 2 4 1
5 1
1 4
3 1 2
4 2 5
输出示例
样例输出
15
24
19
其他说明
数据范围与提示
对于 100% 的数据, 1<=n,m,k,ai<=10^5。数据有一定梯度。
思路:
如果没有换根,这是一道板子题,有了换根呢,就有一些思考难度了
我们发现换根对于2,5是没有任何影响的,显而易见
对于3,4来说,我们需要分类讨论
设根节点=r,输出的结点为u
如果u==r,这个子树里面包含所有的数
如果r不属于u这个子树,那么换根不对操作有任何的影响,显而易见
反之,这个子树就是所有结点删掉以和r相连且是u的子节点(当然可以是结点r)为根的所有点
其余就是模板操作了
上代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
#define MAXN 1000500
#define rep(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
int n,fa[MAXN],to[MAXN],tot,nxt[MAXN],fir[MAXN],a[MAXN],root,m;
int son[MAXN],siz[MAXN],seg[MAXN],rk[MAXN],cnt,dep[MAXN],top[MAXN];
struct Segment_Tree{
int sum[MAXN<<2],add[MAXN<<2];
void work(int k,int l,int r,int z){
add[k]+=z;
sum[k]+=(r-l+1)*z;
}
void push_down(int k,int l,int r,int mid){
if(!add[k]) return;
work(k<<1,l,mid,add[k]); work((k<<1)|1,mid+1,r,add[k]);
add[k]=0;
}
void pre(int k,int l,int r){
add[k]=0;
if(l==r){
sum[k]=a[rk[l]];
return;
}
int mid=(l+r)>>1;
pre(k<<1,l,mid); pre((k<<1)|1,mid+1,r);
sum[k]=sum[k<<1]+sum[(k<<1)|1];
}
void pls(int k,int l,int r,int x,int y,int z){
if(x<=l && r<=y){
work(k,l,r,z);
return;
}
int mid=(l+r)>>1;
push_down(k,l,r,mid);
if(mid>=x) pls(k<<1,l,mid,x,y,z);
if(mid<y) pls((k<<1)|1,mid+1,r,x,y,z);
sum[k]=sum[k<<1]+sum[(k<<1)|1];
}
int find(int k,int l,int r,int x,int y){
if(x<=l && r<=y) return sum[k];
int mid=(l+r)>>1,s=0;
push_down(k,l,r,mid);
if(mid>=x) s+=find(k<<1,l,mid,x,y);
if(mid<y) s+=find((k<<1)|1,mid+1,r,x,y);
return s;
}
}Q;
void dfs1(int x,int f){
dep[x]=dep[f]+1;
siz[x]=1;
for(int k=fir[x];k;k=nxt[k]){
if(to[k]==f) continue;
dfs1(to[k],x);
siz[x]+=siz[to[k]];
if(siz[to[k]]>siz[son[x]]) son[x]=to[k];
}
}
void dfs2(int x,int y){
seg[x]=++cnt;
rk[cnt]=x;
top[x]=y;
if(!son[x]) return;
dfs2(son[x],y);
for(int k=fir[x];k;k=nxt[k]) if(to[k]!=fa[x] && to[k]!=son[x]) dfs2(to[k],to[k]);
}
void work1(int x,int y,int z){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
Q.pls(1,1,n,seg[top[x]],seg[x],z); x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
Q.pls(1,1,n,seg[y],seg[x],z);
}
void work2(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans+=Q.find(1,1,n,seg[top[x]],seg[x]); x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
ans+=Q.find(1,1,n,seg[y],seg[x]);
printf("%lld\n",ans);
}
int check2(int xx,int yy){
int rt=xx,lst=yy;
while(top[xx]!=top[yy]){
if(dep[top[xx]]<dep[top[yy]]) swap(xx,yy);
lst=top[xx];xx=fa[top[xx]];
}
if(dep[xx]>dep[yy]) swap(xx,yy);
if(xx!=rt) return 0;
if(fa[lst]==xx) return lst;
return son[xx];
}
signed main(){
//freopen("2.out","w",stdout);
scanf("%lld",&n);
rep(i,1,n) scanf("%lld",&a[i]);
rep(i,2,n){
scanf("%lld",&fa[i]);
to[++tot]=i;
nxt[tot]=fir[fa[i]];
fir[fa[i]]=tot;
}root=1;
dfs1(1,0);
dfs2(1,1);
Q.pre(1,1,n);
scanf("%lld",&m);
while(m--){
int p,u,v,k;scanf("%lld",&p);
if(p==1) scanf("%lld",&root);
else if(p==2){
scanf("%lld%lld%lld",&u,&v,&k);
work1(u,v,k);
}
else if(p==3){
scanf("%lld%lld",&u,&k);
if(u==root){Q.work(1,1,n,k);continue;}
v=check2(u,root);
if(v==0) Q.pls(1,1,n,seg[u],seg[u]+siz[u]-1,k);
else{
Q.work(1,1,n,k); Q.pls(1,1,n,seg[v],seg[v]+siz[v]-1,-k);
}
}
else if(p==4){
scanf("%lld%lld",&u,&v);
work2(u,v);
}
else{
scanf("%lld",&u);
if(u==root){printf("%lld\n",Q.sum[1]);continue;}
v=check2(u,root);
if(!v) printf("%lld\n",Q.find(1,1,n,seg[u],seg[u]+siz[u]-1));
else{
printf("%lld\n",Q.sum[1]-Q.find(1,1,n,seg[v],seg[v]+siz[v]-1));
}
}
}
return 0;
}
3.P2486 [SDOI2011]染色
题目描述
原题来自:SDOI 2011
给定一棵有 n 个节点的无根树和 m 个操作,操作共两类。
-
将节点 a 到节点 b 路径上的所有节点都染上颜色;
-
询问节点 a 到节点 b 路径上的颜色段数量,连续相同颜色的认为是同一段,例如
112221由三段组成:11、222、1。
请你写一个程序依次完成操作。
输入格式
第一行包括两个整数 n,m,表示节点数和操作数;
第二行包含 n 个正整数表示 n 个节点的初始颜色;
接下来若干行包含两个整数 x 和 y,表示 x 和 y 之间有一条无向边;
接下来若干行每行描述一个操作:
-
C a b c表示这是一个染色操作,把节点 a 到节点 b 路径上所有点(包括 a 和 b)染上颜色; -
Q a b表示这是一个询问操作,把节点 a 到节点 b 路径上(包括 a 和 b)的颜色段数量。
输出格式
对于每个询问操作,输出一行询问结果。
样例
样例输入
6 5
2 2 1 2 1 1
1 2
1 3
2 4
2 5
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5样例输出
3
1
2数据范围与提示
对于 100% 的数据,N,M≤10^5, 所有颜色 C 为整数且在 [0,10^9]之间。
依旧是一道蒟蒻题目,线段树里记录区间不同段数和左右端点颜色,然后tree剖即可,不过代码量很大,很考验代码能力
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define dwn(i,a,b) for(int i=a;i>=b;i--)
#define MAXN 100500
using namespace std;
int rk[MAXN],seg[MAXN],top[MAXN],fa[MAXN],son[MAXN],siz[MAXN],dep[MAXN];
int to[MAXN<<1],tot,fir[MAXN],nxt[MAXN<<1],a[MAXN],n,m,cnt;
struct zlk{
int lt,rt,s;
};
struct Segment_Tree{
int lft[MAXN<<2],rgh[MAXN<<2],sum[MAXN<<2],add[MAXN<<2];
void push_up(int k){
sum[k]=sum[k<<1]+sum[(k<<1)|1];
lft[k]=lft[k<<1]; rgh[k]=rgh[(k<<1)|1];
if(lft[(k<<1)|1]==rgh[k<<1]) --sum[k];
}
void pre(int k,int l,int r){
add[k]=0;
if(l==r){
rgh[k]=lft[k]=a[rk[l]];
sum[k]=1;
return;
}
int mid=(l+r)>>1;
pre(k<<1,l,mid); pre((k<<1)|1,mid+1,r);
push_up(k);
}
void push_down(int k,int mid){
if(!add[k]) return;
sum[k<<1]=1; sum[(k<<1)|1]=1;
add[k<<1]=add[(k<<1)|1]=add[k];
lft[k<<1]=lft[(k<<1)|1]=rgh[k<<1]=rgh[(k<<1)|1]=add[k];
add[k]=0;
}
void change(int k,int l,int r,int x,int y,int z){
if(x<=l && r<=y){
lft[k]=rgh[k]=z;
sum[k]=1;
add[k]=z;
return;
}
if(l==r) return;
int mid=(l+r)>>1;
push_down(k,mid);
if(mid>=x) change(k<<1,l,mid,x,y,z);
if(mid<y) change((k<<1)|1,mid+1,r,x,y,z);
push_up(k);
}
zlk find(int k,int l,int r,int x,int y){
zlk res;
if(x<=l && r<=y){
res.s=sum[k]; res.lt=lft[k]; res.rt=rgh[k];
return res;
}
int mid=(l+r)>>1;
push_down(k,mid);
if(mid>=x && mid<y){
zlk res1=find(k<<1,l,mid,x,y),res2=find((k<<1)|1,mid+1,r,x,y);
res.lt=res1.lt; res.rt=res2.rt; res.s=res2.s+res1.s;
if(res1.rt==res2.lt) res.s--;
return res;
}
if(mid>=x) return find(k<<1,l,mid,x,y);
if(mid<y) return find((k<<1)|1,mid+1,r,x,y);
}
}Q;
void ade(int u,int v){
to[++tot]=v;
nxt[tot]=fir[u];
fir[u]=tot;
}
void dfs1(int x,int f){
dep[x]=dep[f]+1;
siz[x]=1;
fa[x]=f;
for(int k=fir[x];k;k=nxt[k]){
if(to[k]!=f){
dfs1(to[k],x);
siz[x]+=siz[to[k]];
if(siz[to[k]]>siz[son[x]]) son[x]=to[k];
}
}
}
void dfs2(int x,int f){
seg[x]=++cnt;
rk[cnt]=x;
top[x]=f;
if(!son[x]) return;
dfs2(son[x],f);
for(int k=fir[x];k;k=nxt[k]) if(to[k]!=fa[x] && to[k]!=son[x]) dfs2(to[k],to[k]);
}
void work1(int x,int y,int z){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
Q.change(1,1,n,seg[top[x]],seg[x],z); x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
Q.change(1,1,n,seg[y],seg[x],z);
}
void work2(int x,int y){
int yx=-1,zy=-1,ans=0;
zlk wyx;
while(top[x]!=top[y]){
if(dep[top[x]]>dep[top[y]]){
wyx=Q.find(1,1,n,seg[top[x]],seg[x]);
ans+=wyx.s;
if(wyx.rt==yx) --ans;
yx=wyx.lt;
x=fa[top[x]];//cout<<wyx.lt<<" "<<wyx.rt<<" "<<wyx.s<<endl;
}
else{
wyx=Q.find(1,1,n,seg[top[y]],seg[y]);
ans+=wyx.s;
if(wyx.rt==zy) --ans;
zy=wyx.lt;
y=fa[top[y]];
}
//cout<<ans<<" "<<yx<<" "<<zy<<" "<<x<<" "<<y<<endl;
}
if(dep[x]<dep[y]){
wyx=Q.find(1,1,n,seg[x],seg[y]);
ans+=wyx.s;
if(wyx.lt==yx) --ans;
if(wyx.rt==zy) --ans;
}
else{
wyx=Q.find(1,1,n,seg[y],seg[x]);
//cout<<wyx.lt<<" "<<wyx.rt<<" "<<wyx.s<<endl;
ans+=wyx.s;
if(wyx.rt==yx) --ans;
if(wyx.lt==zy) --ans;
}
printf("%lld\n",ans);
}
signed main(){
scanf("%lld%lld",&n,&m);
rep(i,1,n) scanf("%lld",&a[i]);
rep(i,1,n-1){
int a,b;
scanf("%lld%lld",&a,&b);
ade(a,b); ade(b,a);
}
dfs1(1,0);
dfs2(1,1);
Q.pre(1,1,n);
// rep(i,1,n) cout<<son[i]<<" "<<seg[i]<<" "<<top[i]<<endl;
// printf("zlk=%d %d %d\n",Q.find(1,1,n,1,3).s,Q.find(1,1,n,1,3).lt,Q.find(1,1,n,1,3).rt);
rep(i,1,m){
char c=getchar();
while(c!='C' && c!='Q') c=getchar();
int f,g,h; scanf("%lld%lld",&f,&g);
if(c=='C') scanf("%lld",&h),work1(f,g,h);
else work2(f,g);
}
return 0;
}
4.P3313 [SDOI2014]旅行
题目描述
S国有N个城市,编号从1到N。城市间用N-1条双向道路连接,满足从一个城市出发可以到达其它所有城市。每个城市信仰不同的宗教,如飞天面条神教、隐形独角兽教、绝地教都是常见的信仰。
为了方便,我们用不同的正整数代表各种宗教, S国的居民常常旅行。旅行时他们总会走最短路,并且为了避免麻烦,只在信仰和他们相同的城市留宿。当然旅程的终点也是信仰与他相同的城市。S国政府为每个城市标定了不同的旅行评级,旅行者们常会记下途中(包括起点和终点)留宿过的城市的评级总和或最大值。
在S国的历史上常会发生以下几种事件:
“CC x c“:城市x的居民全体改信了c教;
“CW x w“:城市x的评级调整为w;
“QS x y“:一位旅行者从城市x出发,到城市y,并记下了途中留宿过的城市的评级总和;
“QM x y“:一位旅行者从城市x出发,到城市y,并记下了途中留宿过的城市的评级最大值。
由于年代久远,旅行者记下的数字已经遗失了,但记录开始之前每座城市的信仰与评级,还有事件记录本身是完好的。请根据这些信息,还原旅行者记下的数字。 为了方便,我们认为事件之间的间隔足够长,以致在任意一次旅行中,所有城市的评级和信仰保持不变。
输入输出格式
输入格式:
输入的第一行包含整数N,Q依次表示城市数和事件数。
接下来N行,第i+l行两个整数Wi,Ci依次表示记录开始之前,城市i的评级和信仰。 接下来N-1行每行两个整数x,y表示一条双向道路。
接下来Q行,每行一个操作,格式如上所述。
输出格式:
对每个QS和QM事件,输出一行,表示旅行者记下的数字。
输入输出样例
说明
N,Q < =10^5 , C < =10^5
数据保证对所有QS和QM事件,起点和终点城市的信仰相同;在任意时
刻,城市的评级总是不大于10^4的正整数,且宗教值不大于C。
思路:
对于一种宗教,我们需要建一棵线段树
如果生建的话很显然会MLE,所以我们要动态开点
即,如果1-2,1-3这样一棵树
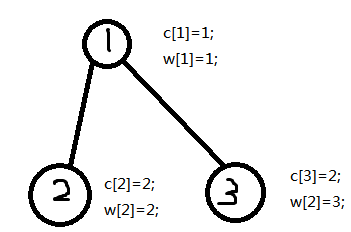
宗教信仰和评分如图所示,当搞1号结点时,我们发现宗教1号线段树的根没有定,于是就将这个根设为++size,然后按照线段树的方法搞即可
然后搞2号结点时,我们发现宗教2号线段树的根没有定,于是就将这个根设为++size,然后按照线段树的方法搞即可
搞3号结点时,宗教2号线段树的根已经定了,直接按照线段树的方法搞即可
可以证明,size的最大值为2*1e5*log(1e5)约=3.3*1e6,然后开一个4倍空间也不会爆内存,
这些东西还是代码清晰
#define MAXN 13000500
int rs[MAXN],ls[MAXN],sum[MAXN],maxn[MAXN];
void init(){
memset(rs,0,sizeof(rs)); memset(ls,0,sizeof(ls));
memset(sum,0,sizeof(sum)); memset(maxn,0,sizeof(maxn));
}
void push_up(int k){
sum[k]=sum[ls[k]]+sum[rs[k]];
maxn[k]=max(maxn[ls[k]],maxn[rs[k]]);
}
void change(int &k,int l,int r,int x,int y){
if(!k) k=++size;
if(l==r && l==x){
sum[k]=maxn[k]=y;
return;
}
if(l==r) return;
int mid=(l+r)>>1;
if(mid>=x) change(ls[k],l,mid,x,y);
else change(rs[k],mid+1,r,x,y);
push_up(k);
}
rep(i,1,n) scanf("%d%d",&w[i],&c[i]);
rep(i,1,n) Q.change(root[c[i]],1,n,seg[i],w[i]);
好的,然后就是普普通通的树剖了
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define MAXN 13000500
#define MAXM 100040
using namespace std;
int size;
int siz[MAXM],top[MAXM],seg[MAXM],dep[MAXM],son[MAXM],fa[MAXM],cnt,rk[MAXM];
int n,tot,w[MAXM],c[MAXM],root[MAXN],fir[MAXM],to[MAXM<<1],nxt[MAXM<<1],m;
struct Segment_Tree{
int rs[MAXN],ls[MAXN],sum[MAXN],maxn[MAXN];
void init(){memset(rs,0,sizeof(rs)); memset(ls,0,sizeof(ls)); memset(sum,0,sizeof(sum)); memset(maxn,0,sizeof(maxn));}
void push_up(int k){
sum[k]=sum[ls[k]]+sum[rs[k]];
maxn[k]=max(maxn[ls[k]],maxn[rs[k]]);
}
void change(int &k,int l,int r,int x,int y){
if(!k) k=++size;
if(l==r && l==x){
sum[k]=maxn[k]=y;
return;
}
if(l==r) return;
int mid=(l+r)>>1;
if(mid>=x) change(ls[k],l,mid,x,y);
else change(rs[k],mid+1,r,x,y);
push_up(k);
}
int find(int k,int l,int r,int x,int y){
if(!k) return 0;
if(x<=l && r<=y) return sum[k];
if(l==r) return 0;
int mid=(l+r)>>1,s=0;
if(mid>=x) s=find(ls[k],l,mid,x,y);
if(mid<y) s+=find(rs[k],mid+1,r,x,y);
return s;
}
int find_max(int k,int l,int r,int x,int y){
if(!k) return 0;
if(x<=l && r<=y) return maxn[k];
if(l==r) return 0;
int mid=(l+r)>>1,s=0;
if(mid>=x) s=find_max(ls[k],l,mid,x,y);
if(mid<y) s=max(s,find_max(rs[k],mid+1,r,x,y));
return s;
}
}Q;
void ade(int a,int b){
to[++tot]=b;
nxt[tot]=fir[a];
fir[a]=tot;
}
void dfs1(int x,int f){
fa[x]=f;
dep[x]=dep[f]+1;
siz[x]=1;
for(int k=fir[x];k;k=nxt[k]){
if(to[k]==f) continue;
dfs1(to[k],x);
siz[x]+=siz[to[k]];
if(siz[to[k]]>siz[son[x]]) son[x]=to[k];
}
}
void dfs2(int x,int y){
seg[x]=++cnt;
rk[cnt]=x;
top[x]=y;
if(!son[x]) return;
dfs2(son[x],y);
for(int k=fir[x];k;k=nxt[k]) if(to[k]!=fa[x] && to[k]!=son[x]) dfs2(to[k],to[k]);
}
void work1(int x,int y){
int s=0,t=c[x];
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
s+=Q.find(root[t],1,n,seg[top[x]],seg[x]); x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
s+=Q.find(root[t],1,n,seg[x],seg[y]);
printf("%d\n",s);
}
void work2(int x,int y){
int s=0,t=c[x];
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
s=max(s,Q.find_max(root[t],1,n,seg[top[x]],seg[x])); x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
s=max(s,Q.find_max(root[t],1,n,seg[x],seg[y]));
printf("%d\n",s);
}
char ck[4];
int main(){
scanf("%d%d",&n,&m);
rep(i,1,n) scanf("%d%d",&w[i],&c[i]);
rep(i,1,n-1){
int a,b; scanf("%d%d",&a,&b);
ade(a,b); ade(b,a);
}
dfs1(1,0); dfs2(1,1);
rep(i,1,n) Q.change(root[c[i]],1,n,seg[i],w[i]);
rep(i,1,m){
int x,y;
scanf("%s%d%d",ck,&x,&y);
if(ck[0]=='C' && ck[1]=='C'){
Q.change(root[c[x]],1,n,seg[x],0);
c[x]=y;
Q.change(root[c[x]],1,n,seg[x],w[x]);
}
else if(ck[0]=='C'){w[x]=y; Q.change(root[c[x]],1,n,seg[x],y);}
else if(ck[0]=='Q' && ck[1]=='S') work1(x,y);
else work2(x,y);
}
return 0;
}

