汉诺塔问题--递归解决方案

一、问题描述:

　　从左到右有 A、B、C 三根柱子，其中 A 柱子上面有从小叠到大的 n 个圆盘，现要求将 A 柱子上的圆盘移到 C 柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数 

　　

 

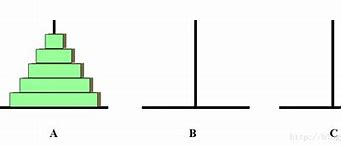
二、思路

　　                                                                      

 

 

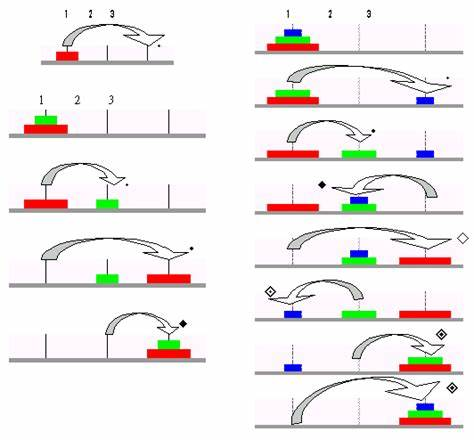
假设现在A柱子上只有一个盘子
                    1号盘子-->C
假设现在A柱子上有两个盘子
                    1号盘子-->B（辅助作用）,
                    2号盘子-->C
                    1号盘子-->C
假设现在A柱子上有三个盘子，把最上面的两个盘子看成一整体，最下面一个看成一个整体
                    上整体全部盘子-->B,
                     最下面盘子-->C，
现在B上面的盘子是两个，和A柱子上两个盘子时状况相同，现在把A柱子(现在是空的)当作辅助柱子，重复上面操作
。。。。。类推

三、代码实现

  

public static void HanNuo(int N,String A,String B,String C){
        if (N==1){
            System.out.println(N+"from"+A+"-->"+C);
            return;
        }
        HanNuo(N-1,A,C,B);//把n-1看成整体，n-1挪动到辅助柱子B上
        System.out.println(N+"from"+A+"-->"+C);//N从A挪动到C
        HanNuo(N-1,B,A,C);//把n-1个盘子的B看成A，A作为辅助柱子
    }