numpy和matplotlib 库学习
开发工具
pycharm 2023.1, 相比vscode和其它工具,该工具对python集成度很高, 需要额外配置环境什么的,非常方便
所需算法库
数学方面函数库的说明: https://www.w3cschool.cn/article/19162038.html
- NumPy: Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。
- SciPy: 建立在 Python 的 NumPy 扩展之上的数学算法和便利函数的集合, 它包括统计,优化,整合,线性代数模块,傅里叶变换,信号和图像处理,常微分方程求解器等等。
- SymPy: 是一个 Python 的科学计算库，用强大的符号计算体系完成诸如多项式求值、求极限、求导、解方程、求积分、解微分方程、级数展开、矩阵运算等计算.
- Pandas: 基于 NumPy的开源库, 为了解决数据分析任务而创建的,主要是为了解决其它编程语言、科研环境的痛点。处理数据一般分为几个阶段：数据整理与清洗、数据分析与建模、数据可视化与制表，Pandas 是处理数据的理想工具。
https://pypandas.cn/docs/, 学习文档 - Matplotlib: Python 中最著名的绘图系统
https://blog.iyatt.com/?p=6766
绘制各个图形方法汇总: https://zhuanlan.zhihu.com/p/363844187 - traitsUI: Python中存在Tkinter，wxPython，pyQt4等GUI图像界面编写库，这三类库要求程序员掌握众多的GUI API函数,对于科学计算的应用来说，我们希望可以快速的开发界面，能够交互的处理程序，而不需要花很多精力在界面响应上，那么TraitsUI就是一个理想的选择
- PyOpenGL: Python绑定到OpenGL及相关接口。绑定是使用标准ctype库创建的，并且是在极其自由的BSD风格的开放源码许可下提供的
官方文档：https://pyopengl.sourceforge.net
相关中文教程：https://www.cnblogs.com/us-wjz/articles/11468789.html
基于QT6的PyOpenGL库, 代码示例
点击查看代码
from PySide6 import QtCore, QtGui, QtWidgets, QtOpenGLWidgets
from OpenGL.GL import *
from OpenGL.GLUT import *
from OpenGL.GLU import *
class openGL_Widget(QtOpenGLWidgets.QOpenGLWidget):
def __init__(self, parent=None):
super().__init__(parent)
# 这个三个是虚函数, 需要重写
# paintGL
# initializeGL
# resizeGL
# 启动时会先调用 initializeGL, 再调用 resizeGL , 最后调用两次 paintGL
# 出现窗口覆盖等情况时, 会自动调用 paintGL
# 调用过程参考 https://segmentfault.com/a/1190000002403921
# 绘图之前的设置
def initializeGL(self):
glClearColor(0, 0, 0, 1)
glEnable(GL_DEPTH_TEST)
glEnable(GL_LIGHT0)
glEnable(GL_LIGHTING)
glColorMaterial(GL_FRONT_AND_BACK, GL_AMBIENT_AND_DIFFUSE)
glEnable(GL_COLOR_MATERIAL)
# 绘图函数
def paintGL(self):
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glBegin(GL_TRIANGLES)
glColor3f(1.0, 0.0, 0.0)
glVertex3f(-0.5, -0.5, 0)
glColor3f(0.0, 1.0, 0.0)
glVertex3f(0.5, -0.5, 0)
glColor3f(0.0, 0.0, 1.0)
glVertex3f(0.0, 0.5, 0)
glEnd()
def resizeGL(self, w, h):
glViewport(0, 0, w, h)
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
gluPerspective(45, w / h, 0.01, 100.0)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
gluLookAt(0, 0, 5, 0, 0, 0, 0, 1, 0)
class Ui_MainWindow(object):
def setupUi(self, MainWindow):
MainWindow.setObjectName("MainWindow")
MainWindow.resize(946, 600)
self.centralwidget = QtWidgets.QWidget(MainWindow)
self.centralwidget.setObjectName("centralwidget")
self.pushButton_display = QtWidgets.QPushButton(self.centralwidget)
self.pushButton_display.setGeometry(QtCore.QRect(10, 270, 91, 31))
self.pushButton_display.setObjectName("pushButton_display")
self.pushButton_clear = QtWidgets.QPushButton(self.centralwidget)
self.pushButton_clear.setGeometry(QtCore.QRect(120, 270, 91, 31))
self.pushButton_clear.setObjectName("pushButton_clear")
self.textEdit_display = QtWidgets.QTextEdit(self.centralwidget)
self.textEdit_display.setGeometry(QtCore.QRect(10, 80, 241, 181))
self.textEdit_display.setObjectName("textEdit_display")
self.widget = openGL_Widget(self.centralwidget)
self.widget.setGeometry(QtCore.QRect(270, 10, 640, 511))
self.widget.setObjectName("widget")
MainWindow.setCentralWidget(self.centralwidget)
self.menubar = QtWidgets.QMenuBar(MainWindow)
self.menubar.setGeometry(QtCore.QRect(0, 0, 946, 23))
self.menubar.setObjectName("menubar")
MainWindow.setMenuBar(self.menubar)
self.statusbar = QtWidgets.QStatusBar(MainWindow)
self.statusbar.setObjectName("statusbar")
MainWindow.setStatusBar(self.statusbar)
self.retranslateUi(MainWindow)
self.pushButton_display.clicked.connect(MainWindow.pushButton_display_click)
self.pushButton_clear.clicked.connect(MainWindow.pushButton_clear_click)
QtCore.QMetaObject.connectSlotsByName(MainWindow)
def retranslateUi(self, MainWindow):
_translate = QtCore.QCoreApplication.translate
MainWindow.setWindowTitle(_translate("MainWindow", "MainWindow"))
self.pushButton_display.setText(_translate("MainWindow", "显示"))
self.pushButton_clear.setText(_translate("MainWindow", "清除"))
# 这里需要用继承的方法. 因为生成的文件可能会因为界面而改变, 直接继承就不用担心代码被覆盖.
class MyPyQT_Form(QtWidgets.QMainWindow, Ui_MainWindow):
def __init__(self, parent=None):
super(MyPyQT_Form, self).__init__(parent=parent)
self.setupUi(self) # 这个是继承.ui文件的类里面来的.
#实现pushButton_click()函数，textEdit是我们放上去的文本框的id
def pushButton_display_click(self):
self.textEdit_display.setText("你点击了按钮")
def pushButton_clear_click(self):
self.textEdit_display.clear()
if __name__ == '__main__':
app = QtWidgets.QApplication(sys.argv)
w = MyPyQT_Form()
w.show()
sys.exit(app.exec())
矩阵相关计算
矩阵和向量
矩阵可以看作是多个列向量组合而成的
矩阵(行列式)计算
https://www.bilibili.com/video/BV1fv411y7YY?p=3&vd_source=122c88b3c9be04538efc857c8bea3d84
还有其它的计算方式
矩阵加减
矩阵相乘
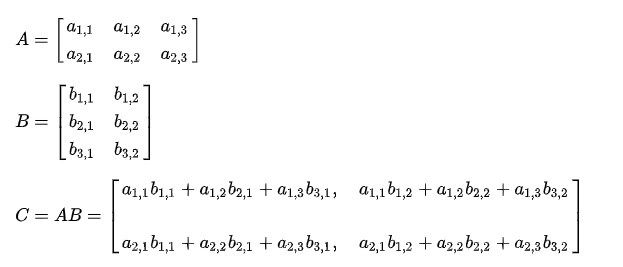
矩阵求逆
- 相当于矩阵相除, 对一个 n 阶方阵 A ，如果存在另一个 n 阶方阵 B，它们满足：AB = BA = E（其中 E 为单位矩阵），那么两矩阵互为逆矩阵。换句话说，A 的逆矩阵为 B ，B 的逆矩阵为 A
- 求逆的方法包括高斯消元、LU分解、矩阵的伴随矩阵等。其中，高斯消元是最常用的方法
应用:
矩阵求逆在算法中有很多应用，以下列举几个常见的例子：
-
线性回归：在线性回归中，需要求解最小二乘问题，即找到一条直线或超平面，使得所有样本点到该直线或超平面的距离平方和最小。通过矩阵求逆，可以求解出最优解。
-
线性规划：在线性规划中，需要求解一个线性函数的最大值或最小值，同时满足一些约束条件。通过矩阵求逆，可以将问题转化为标准形式，然后使用单纯形法求解。
-
矩阵分解：在推荐系统中，通过矩阵分解，可以将用户-物品评分矩阵分解为两个低维矩阵，从而实现推荐功能。其中，矩阵求逆是求解分解后的矩阵的关键步骤之一。
-
神经网络：在神经网络中，需要通过反向传播算法更新权重和偏置，从而实现模型的学习。通过矩阵求逆或者矩阵分解，可以快速计算梯度，加速模型的训练过程。
矩阵转置
定义：将矩阵A的行换成同序号的列所得到的新矩阵称为矩阵A的转置矩阵，记作或．
应用:
- 矩阵乘法：在矩阵乘法中，转置可以用于优化计算过程，例如，当计算A * B时，可以先将B矩阵转置，然后对A的每一行和B的每一列+ 进行点乘，从而减少内存访问的次数和缓存未命中的情况，提高计算效率。
- 图像处理：在图像处理中，可以将图像矩阵进行转置，以便于对图像进行旋转、镜像等操作，从而实现图像的变换。
- 特征提取：在机器学习和数据挖掘中，可以对数据矩阵进行转置，以便于提取数据的特征，例如，在PCA降维算法中，可以对数据矩阵进行转置，从而得到数据的协方差矩阵，进而进行特征值分解。
- 矩阵求逆：在矩阵求逆中，转置可以用于计算伴随矩阵，从而求得矩阵的逆。
矩阵内积
矩阵的内积，也叫点积或者数量积，是两个矩阵对应元素相乘后再相加的结果。A和 B必须是同型矩阵
同时矩阵的内积: 内积的过程 可以看作是多个列向量组的线性组合, 而称内积出的值能够被向量组线性表示
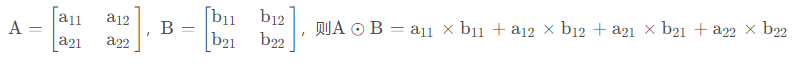
应用
- 神经网络：在神经网络中，内积被广泛应用于计算神经元之间的权重和输入的点积。通过对输入数据矩阵和权重矩阵进行内积运算，可以得到每个神经元对输入信号的响应值。
- 图像处理：在图像处理中，内积可以用于计算两张图片之间的相似度，例如，可以将两张图片的像素矩阵进行内积运算，得到它们的相似度分数。
- 机器学习：在机器学习中，内积经常用于计算数据的相似度，例如，在文本分类中，可以将每篇文本表示为一个向量，然后通过计算向量之间的内积来判断它们之间的相似度。
- 特征提取：在特征提取中，内积可以用于计算数据之间的相关性。例如，在PCA降维算法中，可以通过计算数据矩阵的协方差矩阵的内积来得到主成分分析的结果。
矩阵外积
要求A的列等于B的行的两个矩阵才可以做外积，外积乘法规则是：A的行乘以B的列，结果仍为矩阵
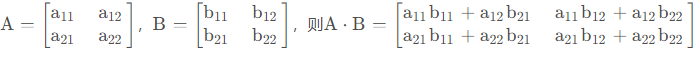
矩阵外积，也叫向量积或叉积，是指将两个向量进行叉乘运算，得到一个新的向量。如果两个向量分别为A和B，则它们的外积可以表示为：
A×B = |A| × |B| × sinθ × n
其中，|A|和|B|分别为向量A和B的模长，θ为A和B之间的夹角，n为垂直于A和B所在平面的单位向量。可以看出，矩阵外积的结果是一个向量，而不是一个标量。
需要注意的是，两个向量进行外积运算时，它们的维数必须相等，并且只有在三维空间中才有意义，因为只有三维空间中才有垂直于两个向量的向量。
矩阵外积也可以表示为矩阵乘法的形式，即：
A×B = [A]x[B]
其中，[A]是一个反对称矩阵。
应用
- 三维图形学：在三维图形学中，矩阵外积常常用于计算法向量，例如，在计算三角形表面的法向量时，可以将两个边向量进行外积运算，得到垂直于该三角形的法向量。
- 机器学习：在机器学习中，矩阵外积可以用于计算两个向量之间的相似度，例如，在计算两个文本向量之间的相似度时，可以将它们进行外积运算，得到它们之间的距离。
- 特征提取：在特征提取中，矩阵外积可以用于计算两个向量之间的相似度，例如，在计算两个音频信号之间的相似度时，可以将它们进行外积运算，得到它们之间的相似度。
API函数笔记记录
numpy 中文文档: https://www.numpy.org.cn/reference/routines/array-creation.html
matplotlib 中文文档: https://matplotlib.net/stable/api/index.html
import numpy as np
import matplotlib.pyplot as plt
plot
plot(X,Y) 创建 Y 中数据对 X 中对应值的二维线图
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
x = np.linspace(0.05, 10, 1000)
y = np.cos(x)
plt.plot(x, y, lw=2, ls=':', label="plot figure")
plt.legend(shadow=True, title="good test")
plt.show()
ls为线条类型
'-', '--', '-.', ':', 'None' 分别表示 '', 'solid', 'dashed', 'dashdot', 'dotted'- lw
lw为宽度 - lable 线条的标识, 需要使用 legend 才可以
legend
标题控制
subplot
import matplotlib.pyplot as plt
import numpy as np
theta=np.arange(0,2*np.pi,0.02)
ax1 = plt.subplot(211, projection='polar')
ax2 = plt.subplot(212)
ax1.plot(theta,theta/6,'--',lw=2)
ax2.plot(theta,theta/6,'--',lw=2)
plt.show()
函数原型
matplotlib.pyplot.subplot(*args, **kwargs)
1. subplot(nrows, ncols, index, **kwargs)
2. subplot(pos, **kwargs)
3. subplot(**kwargs)
4. subplot(ax)
- nrows: 默认1, 设置图表行数
- ncols: 默认1, 设置图表列数
- index: 设置图标序列
nrows和ncols和index可以和三为1, 如如 221表示
arange 和 reshape
- arange(start, stop, step, dtype) 给定间隔内返回均匀的值, start, stop, step(步进), dtype(数据类型)
- reshape(x, y) 显示形式, 以阵列 x, y 显示, 当为 -1 时, 会根据另外一个值自动计算扩展
x = np.arange(0, 20, 0.1)
print(x)
y = np.sin(x)
plt.plot(x,y)
plt.show()
- linspace: 返回指定间隔内的等隔数字
... 等
随机数生成
x = np.random.randint(1,10) #返回一个随机数
x = np.random.randint(1,10, 2) #返回两个随机数
x = np.random.randint(1,10,(4,4))#返回4*4的阵列,随机数 1~10
x = np.random.uniform(1,10,(m,n))#返回m*n阵列,随机数在1~10分布均匀的浮点数
x = np.random.normal(1,10,(m,n))#返回m*n阵列,符合正态分布值0 方差1
x = np.random.randn(10) #返回10个数,符合标准正态分布
x = np.random.randn(2,10) #返回两组十个数,符合标准正态分布
数组和矩阵之间转换
cnnker = [[1, 0, 0],
[0, 1, 0],
[0, 0, 1]] #dtype: list
y = np.array(cnnker) #dtype: tuple, 数组
print(y)
y = np.mat(y) #将数组或者list转换矩阵
print(y)
print("y.T: ")
print(y.T) #矩阵转置T
print("y.I: ")
print(y.I) #矩阵求逆
矩阵求逆的作用: 类似于单个数据的除法, 计算过程
坐标的处理
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-3,3,50)
y1 = 2*x+1
y2 = x**2
#绘制在同一个figure中
plt.figure()
plt.plot(x,y1)
plt.plot(x,y2,color='red',linewidth = 2.0,linestyle = '--')#指定颜色,线宽和线型
ax = plt.gca() # 获取当前坐标的位置
ax.spines['right'].set_color('None') # 设置右边界无
ax.spines['top'].set_color('None') # 设置上边界无
ax.xaxis.set_ticks_position('bottom') # 设置bottom为x轴
ax.yaxis.set_ticks_position('left') # 设置left为y轴
ax.spines['bottom'].set_position(('data',0))#这个位置的括号要注意
ax.spines['left'].set_position(('data',0))
#截取x,y的某一部分
# plt.xlim((-1,2))
# plt.ylim((-2,3))
plt.show()
图像卷积算法示例代码
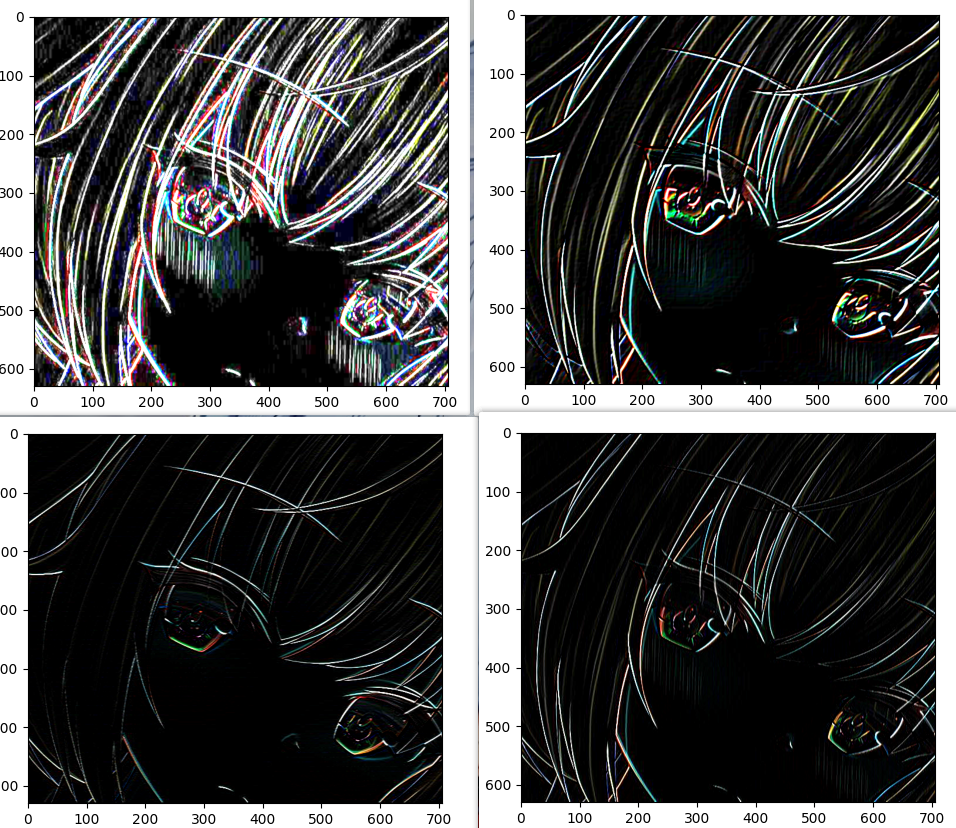
对图片的矩阵内积, 对卷积核(算子)的设置查看效果, 用于边沿检测和特征提取
import matplotlib.pyplot as plt
import pylab
import cv2
import numpy as np
if __name__ == '__main__':
img = plt.imread("test1.jpg") # 在这里读取图片
plt.imshow(img) # 显示读取的图片
pylab.show()
# fil = np.array([[1, 2, 1], # 这个是设置的滤波，也就是卷积核
# [2, -4, 2],
# [1, 2, 1]])
# Prewitt算子
# fil = np.array([[-1, 0, 1], # 这个是设置的滤波，也就是卷积核
# [-1, 0, 1],
# [-1, 0, 1]])
# fil = np.array([[1, 1, 1], # 这个是设置的滤波，也就是卷积核
# [0, 0, 0],
# [-1, -1, -1]])
# fil = np.array([[1, 1, 1], # 这个是设置的滤波，也就是卷积核
# [1, -7, 1],
# [1, 1, 1]])
fil = np.array([[-1, -1, -1, -1, 0], # 边沿检测
[-1, -1, -1, 0, 1],
[-1, -1, 0, 1, 1],
[-1, 0, 1, 1, 1],
[0, 1, 1, 1, 1],
])
res = cv2.filter2D(img, -1, fil) # 使用opencv的卷积函数
plt.imshow(res) # 显示卷积后的图片
# plt.imsave("res1.jpg", res)
pylab.show()
本文来自博客园踩坑狭，作者：韩若明瞳，转载请注明原文链接：https://www.cnblogs.com/han-guang-xue/p/17276134.html
