算法-01基础算法
- 上课理解思路 -> 下课理解背过代码模板 -> 做3-5遍题目(循环AC)
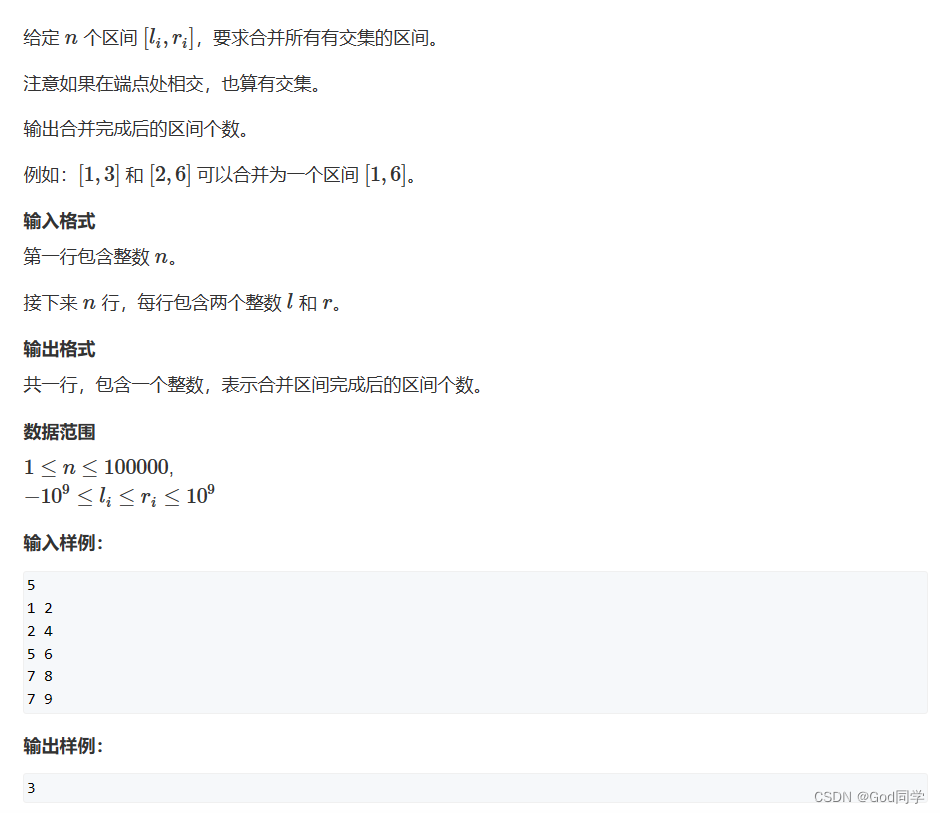
排序
快速排序
快速排序模板题例题
分治:用一个数来分,不需要必须是中心数
先分完再递归两边
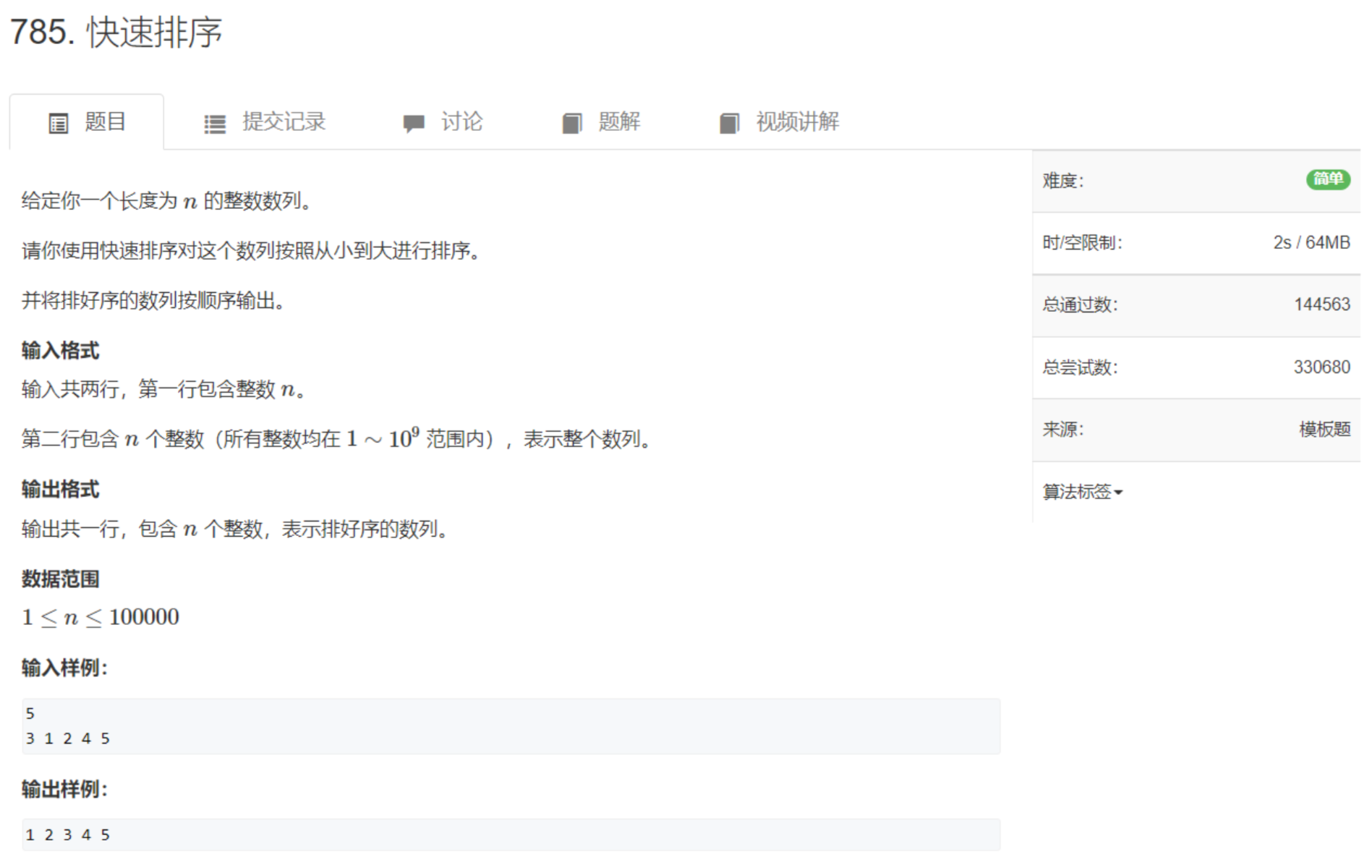
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 数组中元素的个数
int[] nums = new int[n]; // 定义数组大小
for(int i=0;i<n;i++){
nums[i] = sc.nextInt(); // 获取数组元素
}
int[] res = quickSort(0,n-1,nums); // 进行快排并把结果保存在res数组中
for(int i=0;i<n;i++){
System.out.print(res[i] + " "); // 输出排序后的结果
}
}
public static int[] quickSort(int l,int r,int[] nums){
// 边界结束条件
// 写成l==r也是可以的
if(l>=r){
return nums;
}
int p = nums[(l+r)/2]; // 1. 确定分界点,不能取到nums[r]因为下面划分区间使用的j
int i = l-1;
int j = r+1;
// 2. 调整范围
while(i<j){
while(nums[++i]<p); // 从左往右找比p大的数
while(nums[--j]>p); // 从右往左找比p小的数
// 此时如果i<j,那么说明找到了满足要求的一组数,交换数组中i,j两个位置的值
if(i<j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
// 3. 递归处理左右两段[l,j]与[j+1,r],上述while结束后i>=j
// 分治法
quickSort(l,j,nums);
quickSort(j+1,r,nums);
return nums;
}
}
第k个数
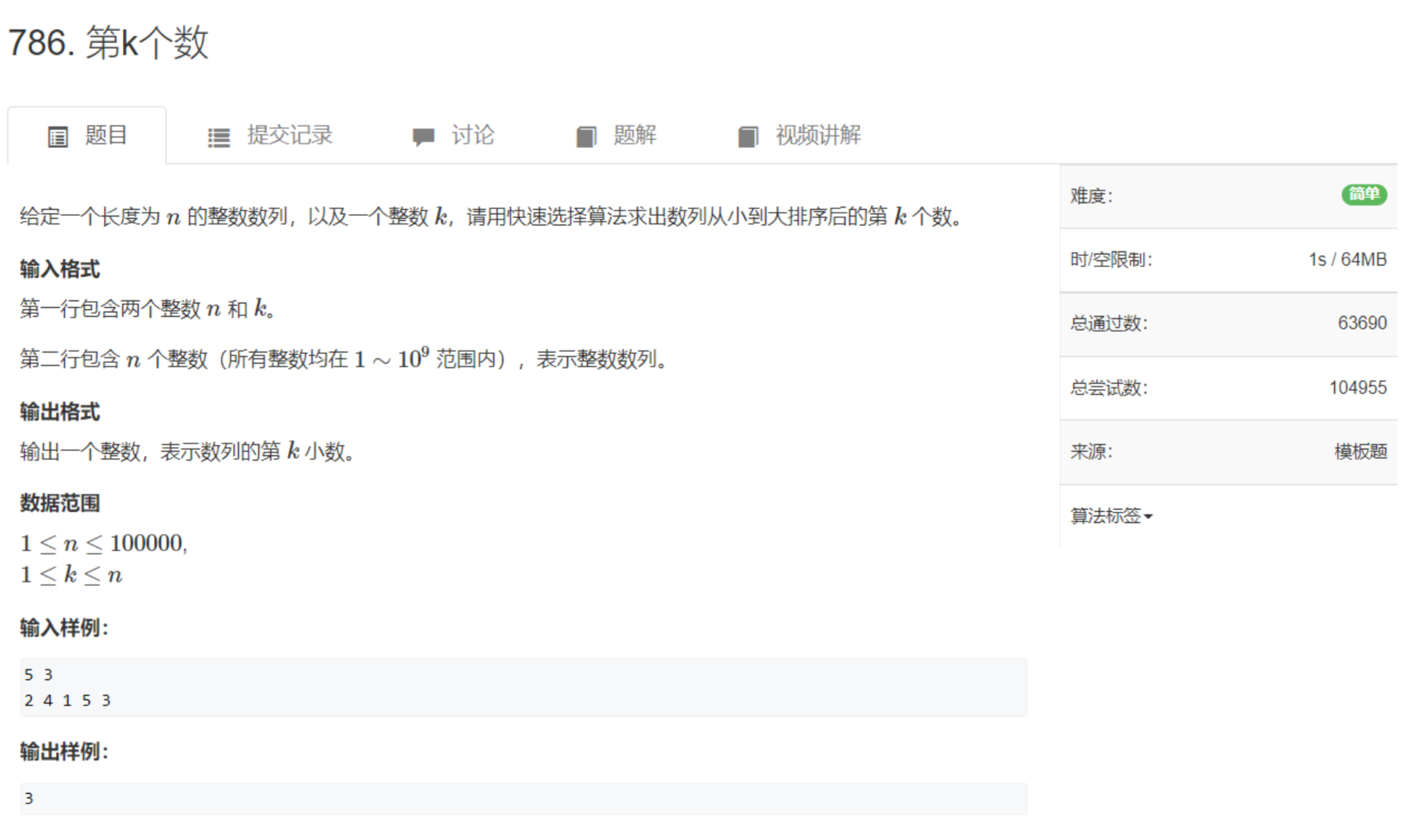
归并排序
归并排序模板题例题
分治:以整个数组的中心点来分
先递归两边再归并
双指针算法,逐个找最小的,存到res数组中
每层都是On,logn分层,总计nlogn
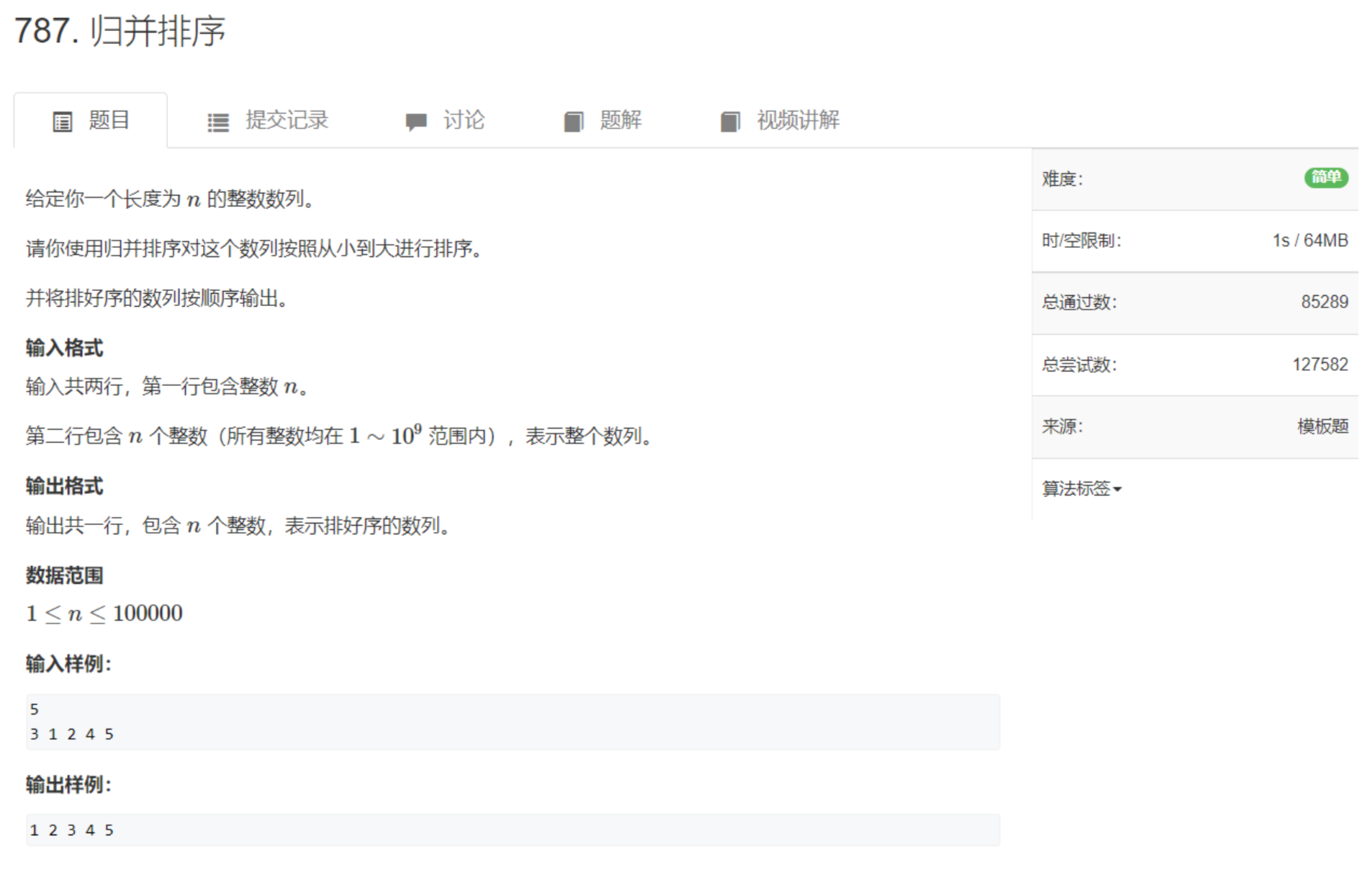
import java.util.*;
public class Main {
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(); // 数组中元素的个数
int[] nums = new int[n]; // 定义数组大小
for (int i = 0; i < n; i++) {
nums[i] = scanner.nextInt(); // 获取数组中的元素
}
merge_sort(0,n-1,nums); // 进行归并排序
for (int i = 0; i < n; i++) {
System.out.print(nums[i] + " ");
}
}
public static void merge_sort (int l,int r,int[] nums) {
if (l>=r) {
return;
}
int mid = (l+r) >> 1;
int i = l,j = mid + 1; // 两个指针指向两段的首元素
merge_sort(l,mid,nums); // 左区间[l,mid]
merge_sort(mid+1,r,nums); // 右区间[mid+1,r]
int[] temp = new int[r - l + 1]; // 临时数组中存储归并后的数据
int k = 0; // 临时数组的指针,用来存储已经排序好的下标位置
while (i <= mid && j <= r) {
if (nums[i] <= nums[j]) {
// temp[k] = nums[i]; // 把较小的数存储到临时数组中
// k++; // 临时数组指针移动
// i++; // 数组指针移动
temp[k++] = nums[i++];
} else {
temp[k++] = nums[j++];
}
}
// 此时说明i中仍有剩余元素,即j已经走完全路程
while (i <= mid) {
temp[k++] = nums[i++]; // 将剩余元素存储到临时数组中
}
// 此时说明j中仍有剩余元素,即i已经走完全路程
while (j <= r) {
temp[k++] = nums[j++]; // 将剩余元素存储到临时数组中
}
// 临时数组归位
for (int q = l,p = 0; q <= r; q++) {
nums[q] = temp[p++];
}
}
}
逆序对的数量
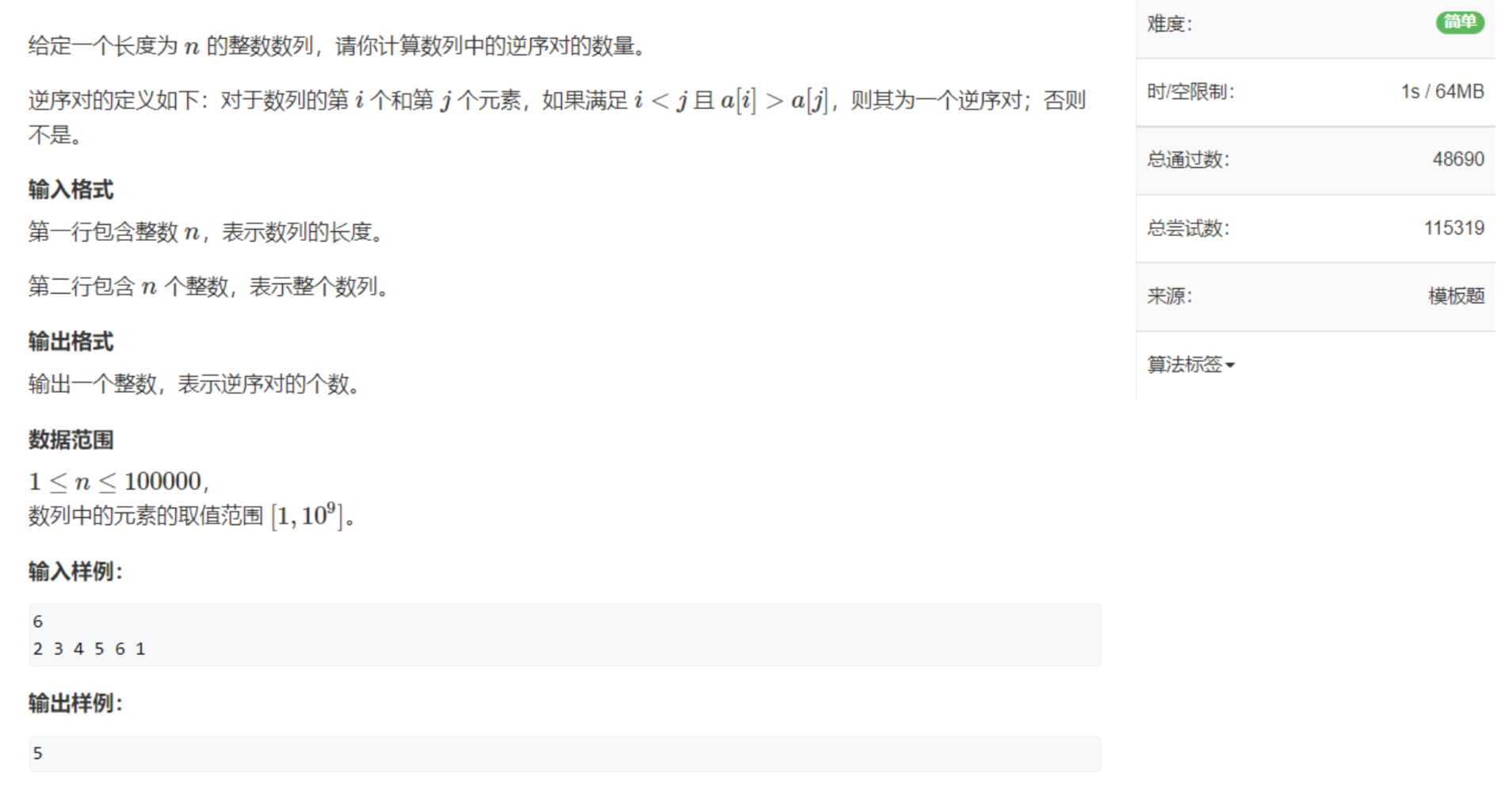
二分法
有单调性可以进行二分,没有也可以
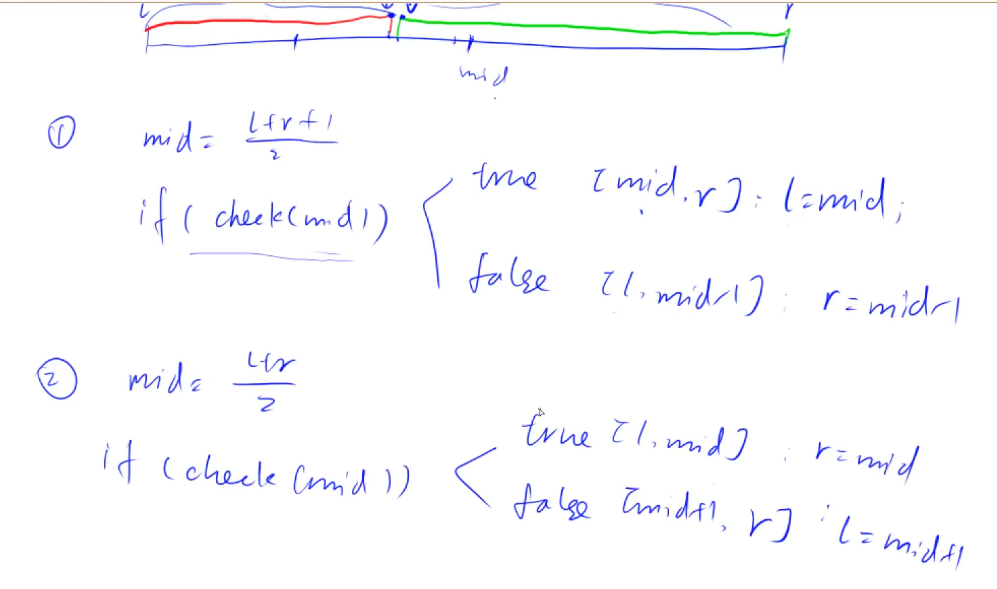
整数二分法
-
第一个大于等于x的数 || 最后一个大于等于x的数
- l=mid,需要补一个1
假设此时l=r-1,那么mid=(l+r)/2=l,在刚好true的时候,l=mid=l,[l,r]没变,则死循环。
如果补1,那么mid=(l+r+1)/2=r,l=mid=r,则刚好结束。 - r=mid,不需要补一个1
- l=mid,需要补一个1
-
整体逻辑
- 先正常写,每次写一个mid,写一个check函数,想一下答案怎么划分,如果l=mid,则需要+1
- check函数:需要选择答案所在的区间,要保证这个区间内部一定有答案

-
起始位置
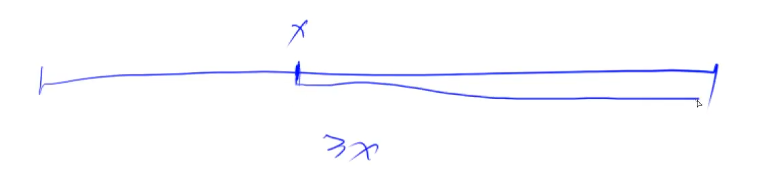
-
终结位置

import java.util.*;
public class Main {
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = scanner.nextInt();
}
for (int i = 0; i < m; i++) {
int x = scanner.nextInt();
// 首先需要找第一个和它相同的数作为起始位置p
int p = 0,q = 0; // 起始位置p(第一次出现),结束位置q(最后一次出现)
int l = 0,r = n-1;
while (l < r) {
int mid = (l+r)>>1;
// 找的是x的起始位置即>=x,更新成[l,mid]
// 最前面那个满足>=x的数就是二分的位置
if (nums[mid] >= x) {
r = mid; // 不用补上+1了
} else {
l = mid+1;
}
}
p = r; // 起始位置(nums[l]==nums[r])
l = 0;
r = n-1;
while (l < r) {
int mid = (l+r+1)>>1;
// 找的是x的最终位置即<=x,更新成[mid,r]
// 最后面那个满足<=x的数就是二分的位置
if (nums[mid] <= x) {
l = mid; // 需要补上+1
} else {
r = mid-1;
}
}
q = r; // 最终位置
if (nums[q] != x) {
System.out.println(-1 + " " + -1);
} else {
System.out.println(p + " " + q);
}
}
}
}
浮点数二分法
import java.util.*;
public class Main {
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
double n = scanner.nextDouble();
// double l = (double)-1e5;
double l = 0;
// double r = 1e5*1.0;
double r = n;
// 当浮点数区间的长度已经很小的时候就已经可以算作答案了
// 浮点数也没有边界的问题
while (r - l > 1e-8) {
double mid = (l+r)/2;
if (mid * mid * mid >= n) {
r = mid;
} else {
l = mid;
}
}
System.out.printf("%.6f",l); // 6位小数就写1e-8,4位就写1e-6
}
}
高精度
- 大整数的存储:用一个数组来存大整数的每一位上的数。
- 这里将大整数的个位,存到数组的第一位,大整数的最高位,存到数组的最后一位,即采用小端序。
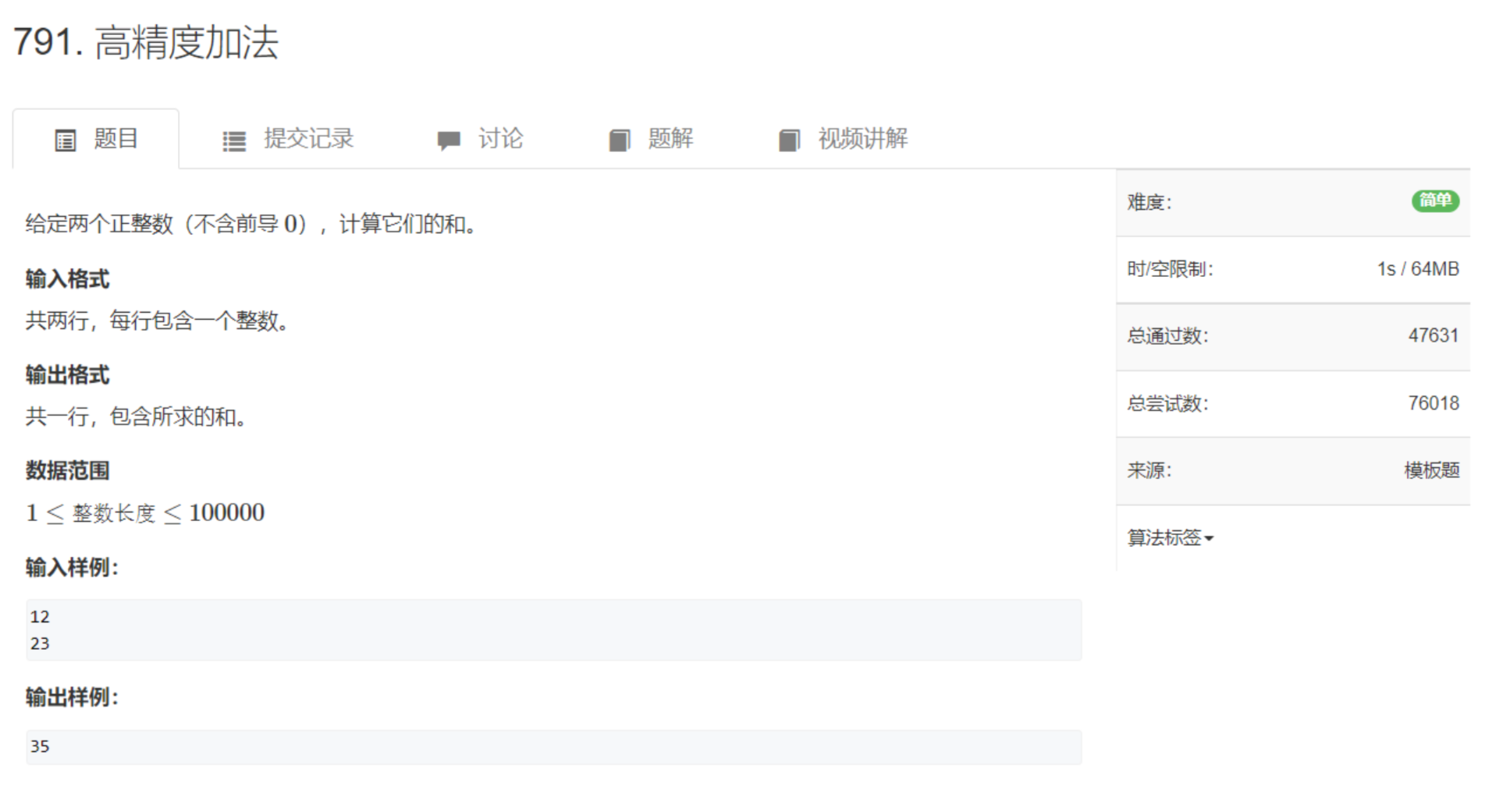
高精度加法
A + B:两个大整数相加
高精度加法的流程,就是模拟人手动做加法的过程,将每一位依次相加,并带上前一位的进位。
import java.io.BufferedInputStream;
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
BigInteger a = scanner.nextBigInteger();
BigInteger b = scanner.nextBigInteger();
System.out.println(a.add(b));
scanner.close();
}
}
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String s1 = scanner.next();
String s2 = scanner.next();
List<Integer> A = new ArrayList<>(s1.length());
List<Integer> B = new ArrayList<>(s2.length());
for (int i = s1.length() - 1; i >= 0; i--) A.add(s1.charAt(i) - '0');
for (int i = s2.length() - 1; i >= 0; i--) B.add(s2.charAt(i) - '0');
List<Integer> C = add(A, B);
for (int i = C.size() - 1; i >= 0; i--) System.out.printf(C.get(i) + "");
}
private static List<Integer> add(List<Integer> A, List<Integer> B) {
List<Integer>C=new ArrayList<>(Math.max(A.size(),B.size())+2);
int t=0;
for(int i=0;i<A.size() || i<B.size();i++){
if(i<A.size())t+=A.get(i);
if(i<B.size())t+=B.get(i);
C.add(t%10);
t/=10;
}
if(t!=0) C.add(t);
return C;
}
}
// java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
public class Main {
private static List<Integer> add(List<Integer> num1, List<Integer> num2) {
int c = 0; // 进位
List<Integer> res = new ArrayList<>();
for (int i = 0; i < num1.size() || i < num2.size(); i++) {
if (i < num1.size()) c += num1.get(i);
if (i < num2.size()) c += num2.get(i);
res.add(c % 10);
c /= 10;
}
// 加完, 看有无进位
if (c > 0) res.add(c);
return res;
}
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String n1, n2;
n1 = reader.readLine();
n2 = reader.readLine();
List<Integer> num1 = new ArrayList<>(), num2 = new ArrayList<>();
for (int i = n1.length() - 1; i >= 0; i--) num1.add(n1.charAt(i) - '0');
for (int i = n2.length() - 1; i >= 0; i--) num2.add(n2.charAt(i) - '0');
List<Integer> res = add(num1, num2);
for (int i = res.size() - 1; i >= 0 ; i--) System.out.print(res.get(i));
}
}
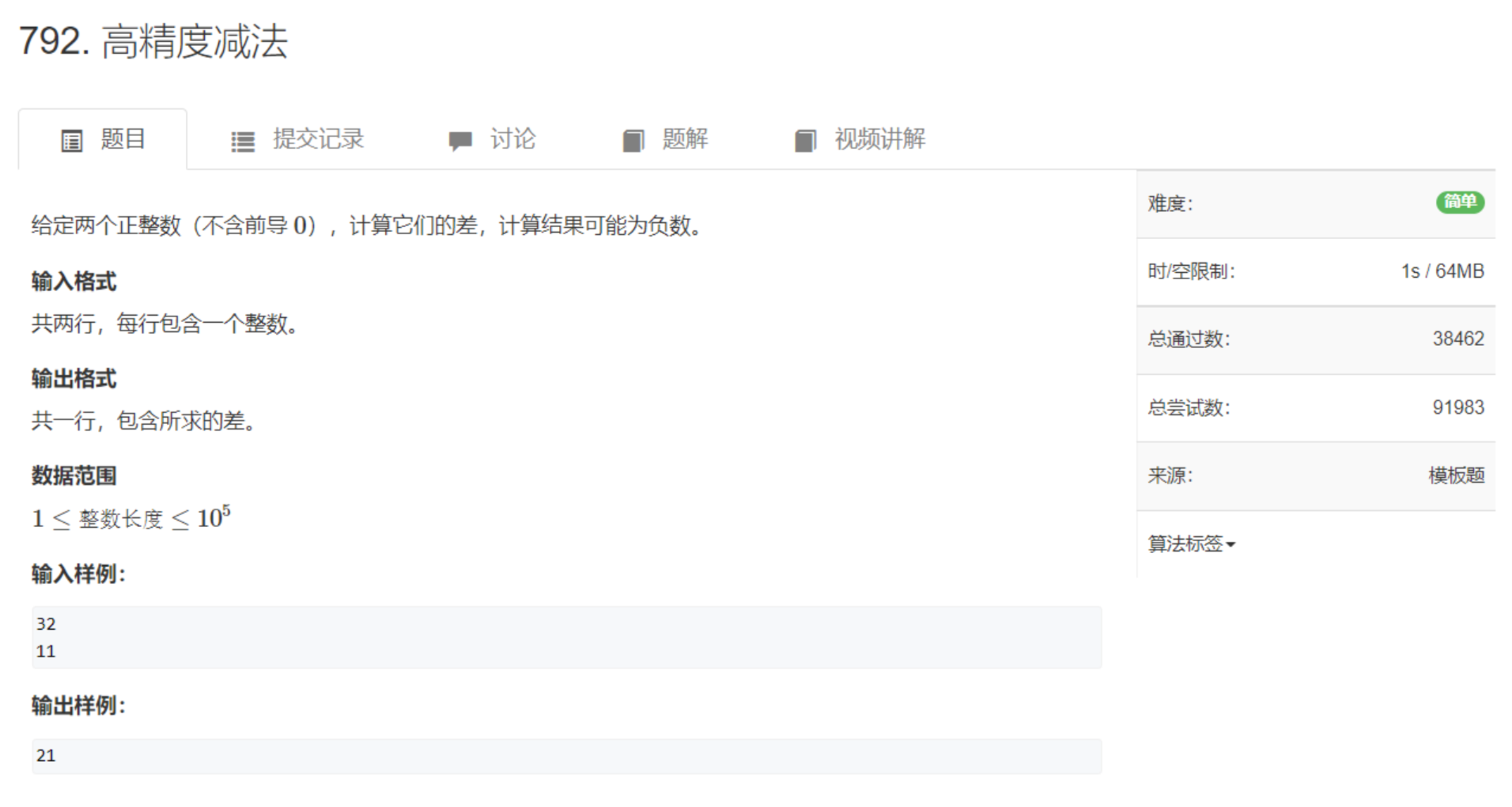
高精度减法
A - B:两个大整数相减
先判断一下A和B的相对大小,若
A >= B,则直接计算减法
A < B,计算B - A,并在结果前面加上负号-
高精度减法的流程,也是模拟人手动做减法的流程,当某一位不够减时,会有借位的概念
import java.io.*;
import java.math.BigInteger;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BigInteger a = new BigInteger(reader.readLine());
BigInteger b = new BigInteger(reader.readLine());
System.out.println(a.subtract(b));
reader.close();
}
}
import java.util.Scanner;
import java.util.List;
import java.util.ArrayList;
public class Main{
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
String s1 = scanner.next();
String s2 = scanner.next();
List<Integer> A = new ArrayList<>();
List<Integer> B = new ArrayList<>();
for(int i = s1.length() - 1;i >= 0;i --) A.add(s1.charAt(i) - '0');
for(int i = s2.length() - 1;i >= 0; i --) B.add(s2.charAt(i) - '0');
if(!cmp(A,B)){
System.out.print("-");
}
List<Integer> C = sub(A,B);
for(int i = C.size() - 1;i >= 0; i --){
System.out.print(C.get(i));
}
}
public static List<Integer> sub(List<Integer> A,List<Integer> B){
if(!cmp(A,B)){
return sub(B,A);
}
List<Integer> C = new ArrayList<>();
int t = 0;
for(int i = 0;i < A.size();i ++){
//这里应该是A.get(i) - B.get(i) - t ,因为可能B为零,所以需要判断一下是不是存在
t = A.get(i) - t;
if(i < B.size()) t -= B.get(i);
C.add((t + 10) % 10);
if(t < 0) t = 1;
else t = 0;
}
//删除指定下标下面的值
while(C.size() > 1 && C.get(C.size() - 1) == 0) C.remove(C.size() - 1);
return C;
}
public static boolean cmp(List<Integer> A,List<Integer> B){
if(A.size() != B.size()) return A.size() > B.size();
/* if(A.size() >= B.size()){
return true;
}else{
return false;
}
*/
for(int i = A.size() - 1;i >= 0;i --){
if(A.get(i) != B.get(i)) {
return A.get(i) > B.get(i);
}
}
return true;
}
}
// java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
public class Main {
public static List<Integer> sub(List<Integer> num1, List<Integer> num2) {
List<Integer> res = new ArrayList<>();
for (int i = 0, t = 0; i < num1.size(); i++) {
t = num1.get(i) - t;
if (i < num2.size()) t -= num2.get(i);
res.add((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
// 去掉前缀的0
while (res.size() > 1 && res.get(res.size() - 1) == 0) res.remove(res.size() - 1);
return res;
}
// 当 num1 >= num2, 返回 true, 否则返回 false
public static boolean cmp(List<Integer> num1, List<Integer> num2) {
if (num1.size() != num2.size()) return num1.size() > num2.size();
else {
for (int i = num1.size() - 1; i >= 0 ; i--) {
if (num1.get(i).intValue() != num2.get(i).intValue()) return num1.get(i) > num2.get(i);
}
return true; // num1 == num2
}
}
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String n1, n2;
n1 = reader.readLine();
n2 = reader.readLine();
List<Integer> num1 = new ArrayList<>(), num2 = new ArrayList<>();
for (int i = n1.length() - 1; i >= 0; i--) num1.add(n1.charAt(i) - '0');
for (int i = n2.length() - 1; i >= 0; i--) num2.add(n2.charAt(i) - '0');
if (cmp(num1, num2)) {
List<Integer> res = sub(num1, num2);
for (int i = res.size() - 1; i >= 0 ; i--) System.out.print(res.get(i));
} else {
List<Integer> res = sub(num2, num1);
System.out.print("-");
for (int i = res.size() - 1; i >= 0 ; i--) System.out.print(res.get(i));
}
}
}
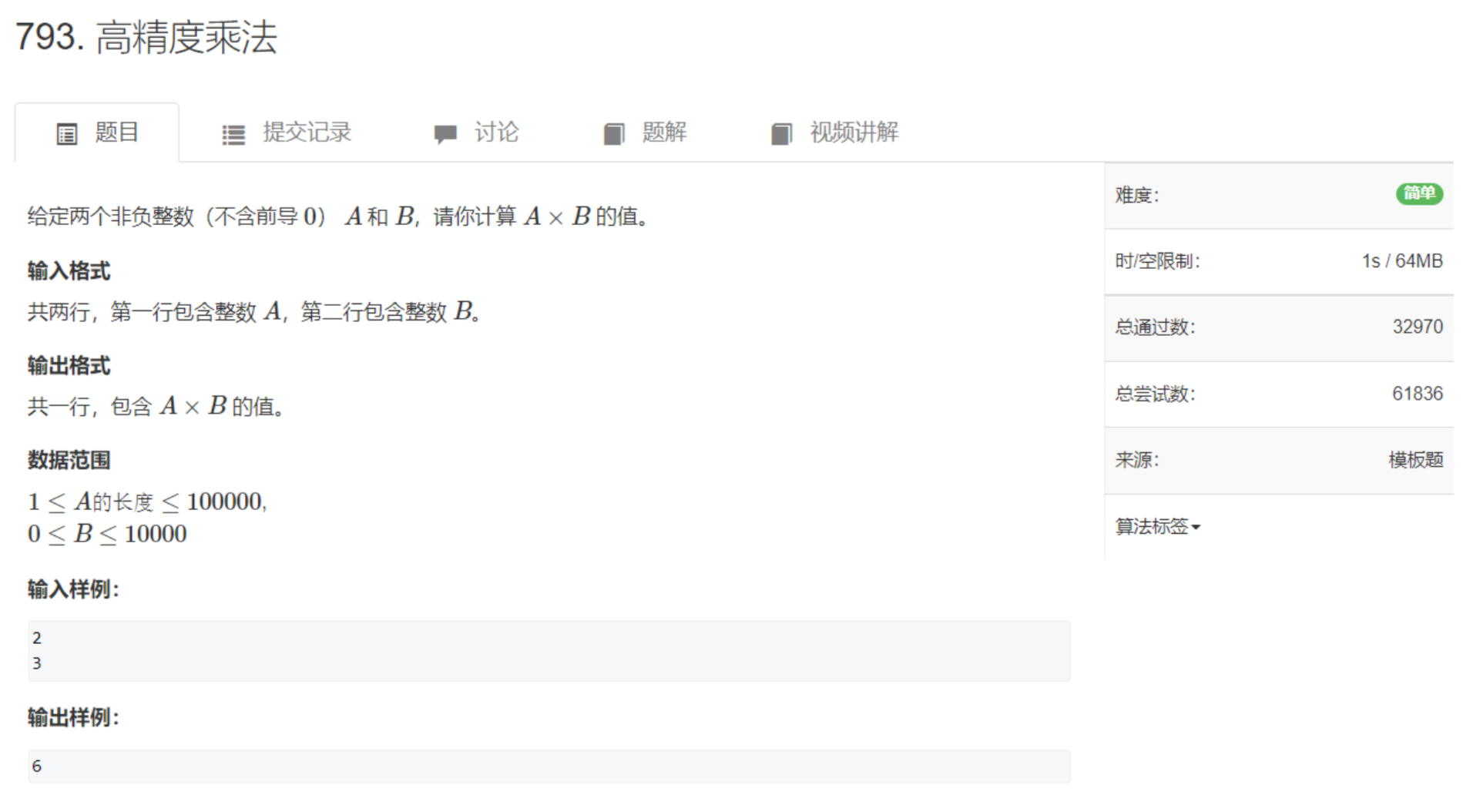
高精度乘法
A × b:一个大整数乘一个小整数
把b看成一个整体,和A的每一位去做乘法。例如:123 × 12。
首先从A的最低位开始,计算3 × 12,得36,则结果中的个位为:36 % 10 = 6,产生的进位为36 / 10 = 3;继续下一位,计算2 × 12,得24,加上进位3,得27,结果中的十位为:27 % 10 = 7,产生的进位是27 / 10 = 2;继续下一位,1 × 12 + 2 = 14,则百位上的结果为14 % 10 = 4,产生进位14 / 10 = 1,则最终结果为1476。
// import java.io.BufferedReader;
// import java.io.IOException;
// import java.io.InputStreamReader;
// import java.io.PrintWriter;
import java.io.*;
import java.math.BigInteger;
public class Main {
static BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
static PrintWriter pw=new PrintWriter(System.out);
public static void main(String args[]) throws IOException{
BigInteger a=new BigInteger(bf.readLine());
BigInteger b=new BigInteger(bf.readLine());
BigInteger res=a.multiply(b);
pw.println(res);
pw.close();
}
}
import java.util.*;
public class Main {
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
String a = scanner.next();
int b = scanner.nextInt();
List<Integer> A = new ArrayList<>(a.length());
for (int i = a.length()-1; i >= 0; i--) A.add(a.charAt(i) - '0');
List<Integer> C = mul(A,b);
for (int i = C.size()-1; i >= 0; i--) System.out.print(C.get(i));
}
public static List<Integer> mul (List<Integer> A,int b) {
List<Integer> C = new ArrayList<>(A.size());
int t = 0;
for (int i = 0; i < A.size(); i++) {
t = t + A.get(i)*b;
C.add(t%10);
t /= 10;
}
while (t != 0) {
C.add(t%10);
t /= 10;
}
while (C.size() > 1 && C.get(C.size()-1) == 0) {
C.remove(C.size() - 1);
}
return C;
}
}
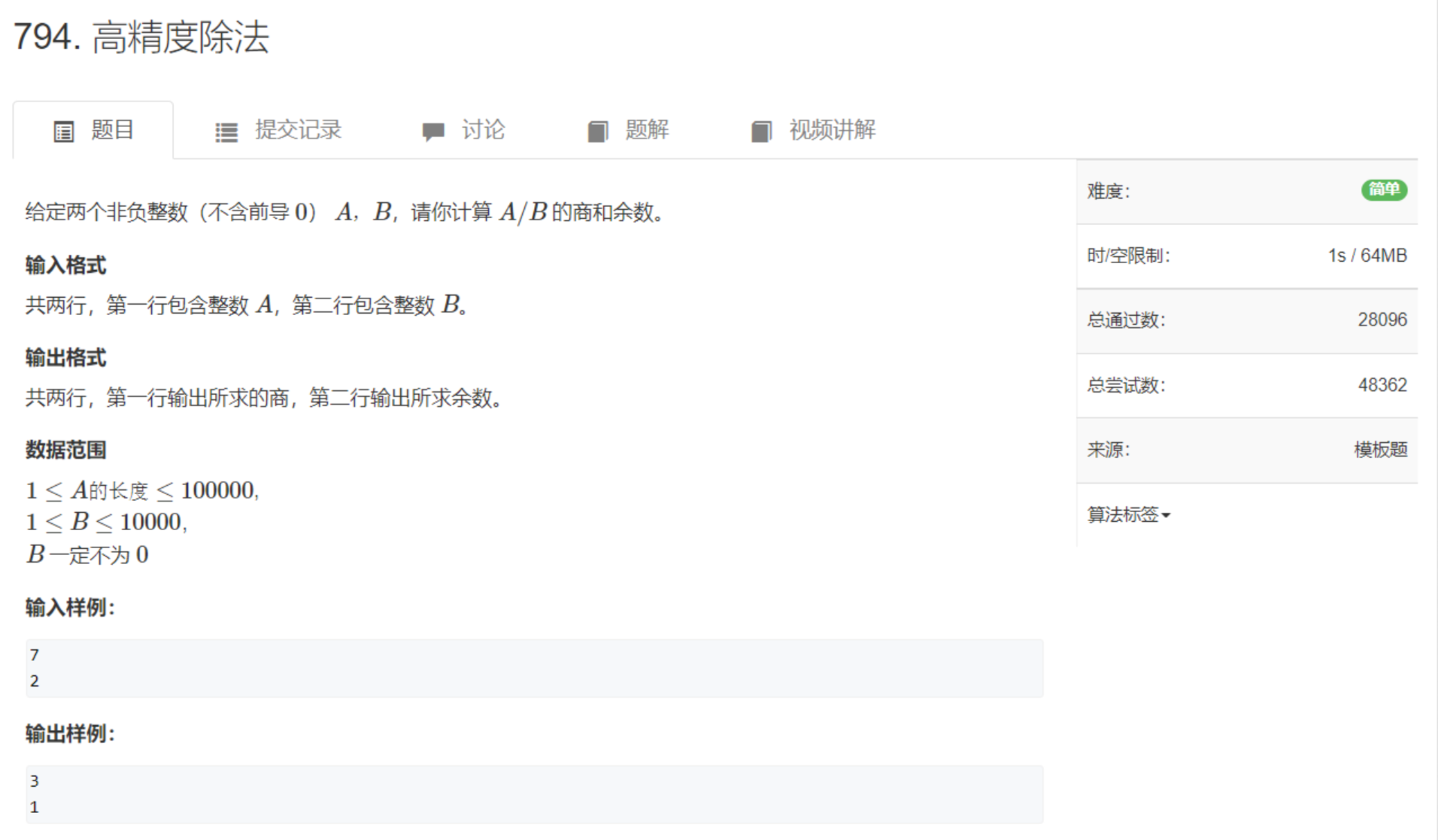
高精度除法
A ÷ b:一个大整数除以一个小整数
算法的流程,是模拟人手动做除法的流程。从最高位除起,依次做商和取余。每一轮的余数,乘以10,加上下一位的数,作为下一轮的被除数。
- 比如123 ÷ 12

// import java.io.BufferedReader;
// import java.io.IOException;
// import java.io.InputStreamReader;
// import java.io.PrintWriter;
import java.io.*;
import java.math.BigInteger;
public class Main {
static BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
static PrintWriter pw=new PrintWriter(System.out);
public static void main(String args[]) throws IOException{
BigInteger a=new BigInteger(bf.readLine());
BigInteger b=new BigInteger(bf.readLine());
BigInteger res1=a.divide(b);
BigInteger res2=a.mod(b);
pw.println(res1);
pw.println(res2);
pw.close();
}
}
// java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Main {
static class Pair {
List<Integer> quotient;
int remainder;
public Pair(List<Integer> quotient, int remainder) {
this.quotient = quotient;
this.remainder = remainder;
}
}
public static Pair div(List<Integer> num1, int num2) {
List<Integer> quotient = new ArrayList<>();
int r = 0;
for (int i = num1.size() - 1; i >= 0 ; i--) {
r = r * 10 + num1.get(i);
quotient.add(r / num2);
r = r % num2;
}
// 反转
Collections.reverse(quotient);
// 去除前缀0
while (quotient.size() > 1 && quotient.get(quotient.size() - 1) == 0) quotient.remove(quotient.size() - 1);
return new Pair(quotient, r);
}
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String n1 = reader.readLine();
int n2 = Integer.parseInt(reader.readLine());
List<Integer> num1 = new ArrayList<>();
for (int i = n1.length() - 1; i >= 0; i--) num1.add(n1.charAt(i) - '0');
Pair res = div(num1, n2);
for (int i = res.quotient.size() - 1; i >= 0 ; i--) System.out.print(res.quotient.get(i));
System.out.printf("\n%d\n", res.remainder);
}
}
前缀和与差分
前缀和
Acwing - 795:前缀和
假设有一个数组:a1,a2,a3,a4,a5,…,an(注意,下标从1开始)
前缀和 Si = a1 + a2 + a3 + … + ai (即前i个数的和)
显然的,前缀和满足 Si = Si-1 + ai ,特殊的,我们可以定义S0 = 0,这样,任何区间[l, r],我们都可以用 Sr - Sl-1 这样的公式来计算,而不需要对边界进行特殊处理(当l = 1时,求[l, r]的所有数的和,其实就是求 Sr)。
前缀和的最大作用,就是用来求任意一段区间的所有数的和。比如,要求区间[l, r]的全部元素的和。若没有前缀和数组,则我们需要遍历原数组,时间复杂度为O(n)。若有前缀和数组,我们只需要计算 Sr - Sl-1,时间复杂度为O(1)。
因为 Sr = a1 + a2 + a3 + … + al-1 + al + … + ar
而 Sl-1 = a1 + a2 + a3 + … + al-1

import java.util.*;
public class Main {
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] a = new int[n+1];
int[] s = new int[n+1];
for (int i = 1; i <= n; i++) { a[i] = scanner.nextInt(); }
s[1] = a[1];
for (int i = 2; i <= n; i++) {
s[i] = a[i] + s[i-1];
}
while (m-- != 0) {
int l = scanner.nextInt();
int r = scanner.nextInt();
System.out.println(s[r]-s[l-1]);
}
}
}
Acwing - 796: 子矩阵的和
假设有如下的矩阵
a11 ,a12,a13,a14,…,a1n
a21,a22,a23,a24,…, a2n
…
…
am1,am2,am3,am4,…,amn
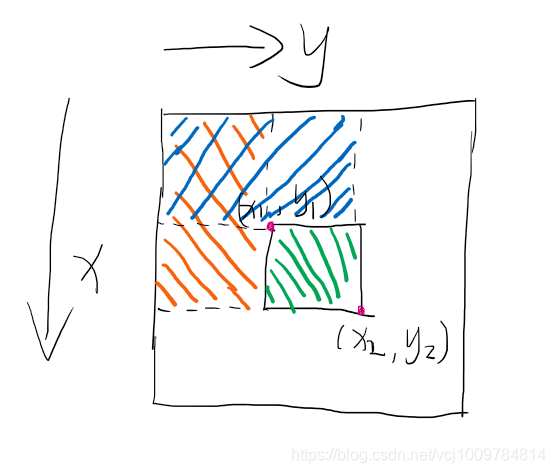
前缀和 Sij 表示点 aij 及其左上角区域的所有数的和。
经过简单推导(面积计算),可以得到 Sij = Si-1,j + Si,j-1 + aij - Si-1,j-1
若要计算左上角边界点为[x1, y1],右下角点为[x2, y2],这2个点之间部分的子矩阵的和(也是求任意一段区间内所有数的和),经过简单推导,能够得到下面的公式
S = Sx2,y2 - Sx1-1,y2 - Sx2,y1-1 + Sx1-1,y1-1(由于矩阵中是离散的点,所以计算时边界需要减掉1)

import java.util.*;
public class Main {
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int q = scanner.nextInt();
int[][] a = new int[n+1][m+1];
int[][] s = new int[n+1][m+1];
for (int i = 1; i <= n; i++){
for (int j = 1; j <= m; j++) {
a[i][j] = scanner.nextInt();
}
}
for(int i = 1 ; i <= n ; i ++ ){
for(int j = 1 ;j <= m ; j ++ ){
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
}
}
while (q-->0) {
int x1 = scanner.nextInt();
int y1 = scanner.nextInt();
int x2 = scanner.nextInt();
int y2 = scanner.nextInt();
System.out.println(s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);
}
}
}
差分
差分,是前缀和的逆运算
Acwing - 797: 差分
假设有一个数组,a1,a2,a3,a4,a5,…,an
针对这个数组,构造出另一个数组,b1,b2,b3,b4,b5,…,bn
使得a数组是b数组的前缀和,即使得 ai = b1 + b2 + … + bi
此时,称b数组为a数组的差分
如何构造b数组呢:
b1 = a1,b2 = a2 - a1,b3 = a3 - a2,…,bn = an - an-1
实际可以不用如此来构造,在输入数组a时,可以先假想数组a和数组b的全部元素都是0。然后每次进行一次插入操作(指的是对数组a的[l, r]区间的每个数加上常数C),比如
对a数组区间[1,1],加(插入)常数a1;对区间[2,2],加常数a2,…,这样在输入数组a的同时,就能够快速构造出其差分数组b
- 差分的作用:
- 若要对a数组中[l, r]区间内的全部元素都加上一个常数C,若直接操作a数组的话,时间复杂度是O(n)。而如果操作其差分数组b,则时间复杂度是O(1)。这是因为,数组a是数组b的前缀和数组,只要对 bl 这个元素加C,则a数组从l位置之后的全部数都会被加上C,但r位置之后的所有数也都加了C,所以我们通过对 br+1 这个数减去C,来保持a数组中r位置以后的数的值不变。
- 于是,对a数组的[l, r]区间内的所有数都加上一个常数C,就可以转变为对 bl 加C,对br+1 减 C。

import java.util.*;
public class Main {
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] nums = new int[n+2];
for (int i = 1; i <= n; i++) {
nums[i] = scanner.nextInt();
}
for (int i = n; i >= 1; i--) {
nums[i] = nums[i]-nums[i-1];
}
for (int i = 0; i < m; i++) {
int l = scanner.nextInt();
int r = scanner.nextInt();
int c = scanner.nextInt();
nums[l] += c;
nums[r+1] -= c;
}
for (int i = 1; i <= n; i++) {
nums[i] += nums[i-1];
System.out.printf("%d ",nums[i]);
}
}
}
Acwing - 798: 差分矩阵
即差分矩阵
对于矩阵a,存在如下一个矩阵b
b11 ,b12,b13,b14,…,b1n
b21,b22,b23,b24,…, b2n
…
…
bm1,bm2,bm3,bm4,…,bmn
使得aij = 矩阵b中[i, j]位置的左上角的所有数的和
称矩阵b为矩阵a的差分矩阵。
同样的,如果期望对矩阵a中左上角为[x1, y1],右下角为[x2, y2]的区域内的全部元素,都加一个常数C,则可以转化为对其差分矩阵b的操作。
先对b中[x1, y1]位置上的元素加C,这样以来,a中[x1, y1]这个点的右下角区域内的所有数都加上了C,但是这样就对[x2, y2]之后的区域也都加了C。我们对[x2, y2]之外的区域需要保持值不变,所以需要进行减法。对bx2+1,y1 减掉C,这样下图红色区域都被减了C,再对bx1,y2+1减掉C,这样下图蓝色区域都被减了C,而红色区域和蓝色区域有重叠,重叠的区域被减了2次C,所以要再加回一个C,即对bx2+1,y2+1 加上一个C。这样,就完成了对[x1, y1],[x2, y2]区域内的所有数(下图绿色区域),都加上常数C。
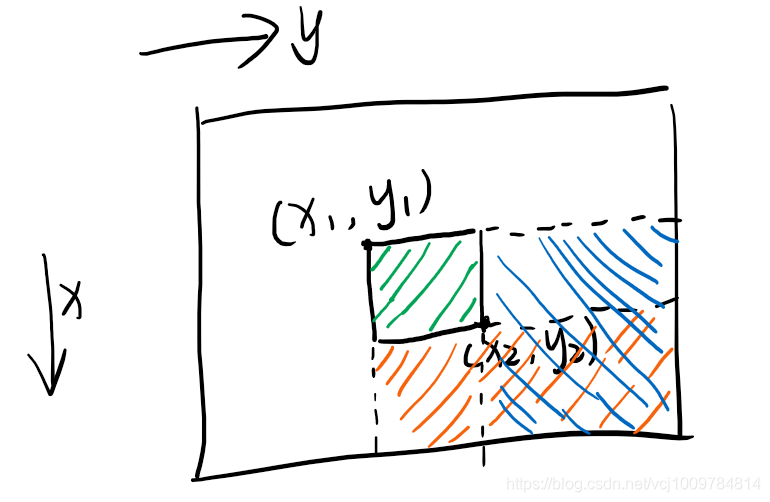
- 总结起来,对原矩阵a,在[x1, y1]到[x2, y2]区域内的全部元素加C,可以转换为对其差分矩阵b做如下操作
- bx1,y1 + C
- bx1,y2+1 - C
- bx2+1,y - C
- bx2+1,y2+1 + C
- 简单记忆为:对b的[x1, y1]加C,对[x2, y2]这个点,分别取x2 + 1,y2 + 1(另一个轴则取y1和x1),减C,然后对[x2 + 1, y2 + 1]加C
- 构造矩阵b,采用与上面相同的方式,先假设矩阵a和矩阵b的元素全都为0,此时矩阵b是矩阵a的差分矩阵,依次进行插入操作即可。
- 即对矩阵a的[1,1]到[1,1],加a[1][1],对[1,2]到[1,2],加a[1][2],…,如此即可构造出矩阵b

import java.util.*;
public class Main {
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int q = scanner.nextInt();
int[][] splits = new int[n+2][m+2];
int[][] sum = new int[n+2][m+2];
for (int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
sum[i][j] = scanner.nextInt();
splits[i][j] = sum[i][j] - sum[i-1][j] - sum[i][j-1] + sum[i-1][j-1];
}
}
for (int i = 0; i < q; i++) {
int x1 = scanner.nextInt();
int y1 = scanner.nextInt();
int x2 = scanner.nextInt();
int y2 = scanner.nextInt();
int c = scanner.nextInt();
splits[x1][y1] += c;
splits[x1][y2+1] -= c;
splits[x2+1][y1] -= c;
splits[x2+1][y2+1] += c;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
sum[i][j] = splits[i][j] + sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1];
System.out.print(sum[i][j] + " ");
}
System.out.println();
}
}
}
小结
- 前缀和是用来:求任意区间的所有数的和,时间复杂度O(1)
- 差分是用来:对任意区间内的所有数加上一个常数,时间复杂度O(1)
- 前缀和与差分互为逆运算
- 前缀和,差分的题目,数组下标从1开始取,可以避免对边界特殊处理。
// 下面称S为a的前缀和数组(矩阵),或者称a为S的差分数组(矩阵)
/*一维
前缀和 Si = Si-1 + ai,数组a任意区间[l, r]的和等于 Sr - Sl-1
差分 ai = Si - Si-1 ,但实际不会这样构造差分数组,直接定义一个函数 insert(int l, int r, int c),表示对S数组的[l, r]区间内的所有数加c。初始时,假想S数组和a数组全为0,对i = 1~n。每次调用insert(i, i, S[i]),即完成对差分数组a的构造。其中insert函数定义如下
*/
void insert(int l, int r, int c) {
// 对前缀和数组S的[l, r]区间的所有元素加上一个常数C, 只需要对S的差分数组a, 对a[l]加C, 对a[r + 1]减C
a[l] += c;
a[r + 1] -= c;
}
/*二维
前缀和 Si,j = Si-1,j + Si,j-1 - Si-1,j-1 + ai,j,矩阵a任意区间[x1, y1]到[x2, y2]的所有元素的和等于Sx2,y2 - Sx1-1,y2 - Sx2,y1-1 + Sx1-1,y1-1
简单记忆为,[x2, y2]的前缀和,减去,取 x2,y2(另一个轴取y1 - 1,x1 - 1)的前缀和,由于有重叠部分被减了2次,所以再加上[x1 - 1, y1 - 1]的前缀和
差分 ai,j ,这里也和一维差分一样的构造方式。直接定义一个函数insert(int x1, int y1, int x2, int y2, int c)。初始时,假想S矩阵和a矩阵全为0,对于每个点[i, j],每次调用insert(i, j, i, j, S[i][j]),即完成对差分矩阵a的构造。其中insert函数定义如下
*/
void insert(int x1, int y1, int x2, int y2, int c) {
a[x1][y1] += c;
a[x2 + 1][y1] -= c;
a[x1][y2 + 1] -= c;
a[x2 + 1][y2 + 1] += c;
}
双指针算法


位运算
离散化

区间合并