FFT与游戏开发(三)
FFT与游戏开发(三)
仅仅是将傅里叶变换的复杂度降到$$O(log(n))$$还不够,能不能再快一点呢?很容易地可以想到,可以将FFT搬到GPU上去实现,这里我实现了一个简单易懂的版本,代码附在最后,有兴趣的同学可以进一步进行优化,例如多尝试使用位运算等。
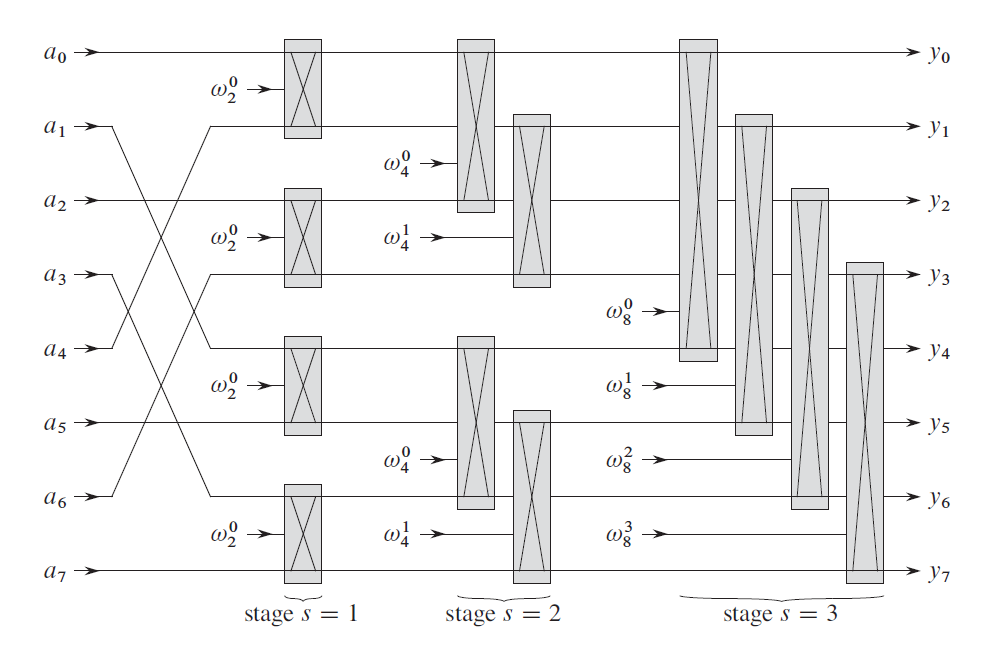
蝶形结构
FFT的蝶形结构很容易使其并行化,而且蝶形结构之间的计算不会互相影响。
Shared Memory
使用shared memory可以保存计算的中间结果,而不用反复地将其存到system memory中,它有着最大32KB的空间。
同步
多个线程同时访问shared memory需要使用GroupMemoryBarrierWithGroupSync/GroupMemoryBarrier进行手动同步.两个同步函数不同的地方在于:
- 不带
WithGroupSync后缀的同步函数,仅仅会保证warp中的线程访问不会出现data race - 而带
WithGroupSync后缀的同步函数,除了保证同一个warp不会出现data race之外,还会同步不同warp中的线程。
除非知道group中所有的线程都会在同一个wrap中执行,否则使用第二种同步方式。
GPUFFT的实现
#pragma kernel FFT
static const uint FFT_DIMENSION = 8;
static const uint FFT_BUTTERFLYS = 4;
static const uint FFT_STAGES = 3;
static const float PI = 3.14159265;
groupshared float2 pingPongArray[FFT_DIMENSION * 2];
RWStructuredBuffer<float2> srcData;
RWStructuredBuffer<float2> dstData;
uint ReverseBits(uint index, uint count) {
return reversebits(index) >> (32 - count);
}
float2 ComplexMultiply(float2 a, float2 b) {
return float2(a.x * b.x - a.y * b.y, a.y * b.x + a.x * b.y);
}
void ButterFlyOnce(float2 input0, float2 input1, float2 twiddleFactor, out float2 output0, out float2 output1) {
float2 t = ComplexMultiply(twiddleFactor, input1);
output0 = input0 + t;
output1 = input0 - t;
}
float2 Euler(float theta) {
float2 ret;
sincos(theta, ret.y, ret.x);
return ret;
}
[numthreads(FFT_BUTTERFLYS, 1, 1)]
void FFT(uint3 id : SV_DispatchThreadID)
{
uint butterFlyID = id.x;
uint index0 = butterFlyID * 2;
uint index1 = butterFlyID * 2 + 1;
pingPongArray[index0] = srcData[ReverseBits(index0, FFT_STAGES)];
pingPongArray[index1] = srcData[ReverseBits(index1, FFT_STAGES)];
uint2 offset = uint2(0, FFT_BUTTERFLYS);
[unroll]
for (uint s = 1; s <= FFT_STAGES; s++) {
GroupMemoryBarrierWithGroupSync();
// 每个stage中独立的FFT的宽度
uint m = 1 << s;
uint halfWidth = m >> 1;
// 属于第几个FFT
uint nFFT = butterFlyID / halfWidth;
// 在FFT中属于第几个输入
uint k = butterFlyID % halfWidth;
index0 = k + nFFT * m;
index1 = index0 + halfWidth;
if (s != FFT_STAGES) {
ButterFlyOnce(
pingPongArray[offset.x + index0], pingPongArray[offset.x + index1],
Euler(-2 * PI * k / m),
pingPongArray[offset.y + index0], pingPongArray[offset.y + index1]);
offset.xy = offset.yx;
} else {
ButterFlyOnce(
pingPongArray[offset.x + index0], pingPongArray[offset.x + index1],
Euler(-2 * PI * k / m),
dstData[index0], dstData[index1]);
}
}
}
参考资料
- Introduction to Algorithms, 3rd
- Understanding Digital Signal Processing
- Practical Rendering and Computation with DirectX11


