FFT与游戏开发(二)
FFT与游戏开发(二)
首先补充下傅里叶变换的原理——把函数分解到一系列正交基上,这些正交基复合下面的条件:
\[\begin{cases}
\int_{-\infty}^{+\infty} f_k(x) f_j(x) \mathrm d x \neq 0 & k=j \\
\int_{-\infty}^{+\infty} f_k(x) f_j(x) \mathrm d x = 0 & k\neq j
\end{cases}
\]
其实这就是一种基的变换,图形学中也有一些变换,如坐标系的变换,球面函数变换到SH,SG等等。
一、从一维DFT到二维DFT
和一维DFT一样,二维DFT所做的事情是把二维空间上的信号分解上二维空间上不同方向的三角函数信号之和。下图解释了这一点。
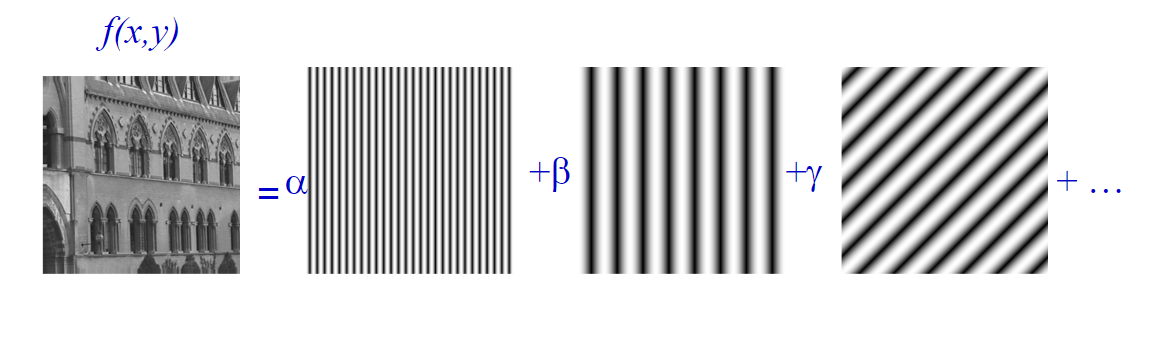
注意到转换后的结果是旋转对称的,一维DFT的结果也可以看出来是对称的。
- 一维DFT的输入
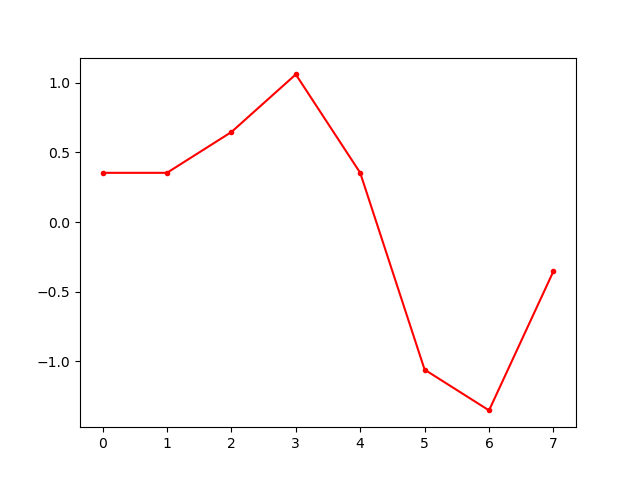
- 一维DFT的输出
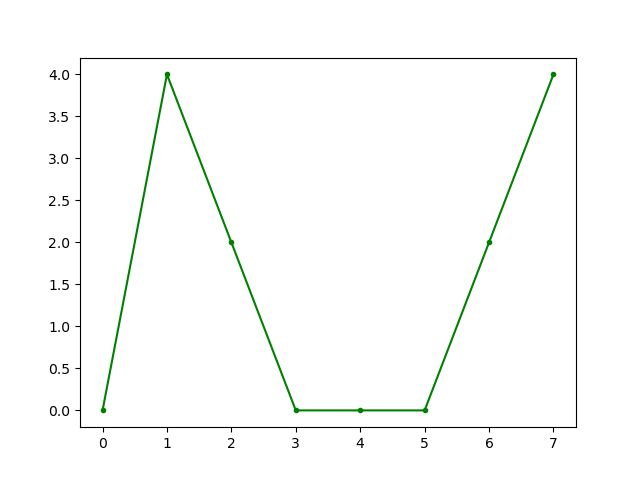
二、二维DFT的可分离特性
原始公式:
\[F(k, l) = \frac{1}{MN} \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f(m, n) e^{-j2\pi
\left(
\frac{k}{M}m + \frac{l}{N}n
\right)}
\]
注意到,这个计算是可分离的,就是可以把二维DFT的计算分成内外两层1维DFT的计算:
\[F(k, l) =
\frac{1}{M} \sum_{m=0}^{M-1} \left[
\frac{1}{N} \sum_{n=0}^{N-1} f(m, n) e^{-j2\pi \frac{ln}{N}}
\right] e^{-j2\pi\frac{km}{M}}
\]
具体做法是,对每行/列元素进行一次DFT之后,对结果的每一列/行再进行一次DFT。



