WebGL学习笔记(二):WebGL坐标系及基础几何概念
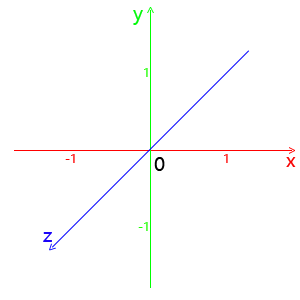
2019-07-17 13:36 阿诚de窝 阅读(3466) 评论(0) 收藏 举报WebGL使用的是正交右手坐标系,且每个方向都有可使用的值的区间,超出该矩形区间的图像不会绘制:
- x轴最左边为-1,最右边为1;
- y轴最下边为-1,最上边为1;
- z轴朝向你的方向最大值为1,远离你的方向最大值为-1;
注:这些值与Canvas的尺寸无关,无论Canvas的长宽比是多少,WebGL的区间值都是一致的。
如图:
向量
点积
p1.x * p2.x + p1.y * p2.y + p1.z * p2.z
两个向量的分量相乘之后再相加的结果,该结果和两个向量的夹角相关;两个向量的点积为0时,表示这两个向量的夹角为90度,即相互垂直或正交,大于0时,表示夹角小于90度,小于0时,表示夹角大于90度;
叉乘
叉乘之后的结果不是一个标量,而是一个新的向量,该结果向量和用来运算叉乘的两个向量所在的平面垂直;该向量即三角形平面的法向量;
齐次坐标
我们表示一个3维空间的向量或点时,一般使用包含3个分量的Vector3来表示,而齐次坐标则多引入了一个分量;
之所以多引入一个分量,是为了在仿射变换中的运算更加的方便,更具体的解说请看下面的文章:
https://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html
https://blog.csdn.net/janestar/article/details/44244849
矩阵
在3D中,一般使用4x4的矩阵。
相乘
矩阵相乘在3D图形中是一个非常重要的运算,在3D中无论是移动、旋转还是缩放大小,都是通过在当前矩阵的基础上乘以一个新的矩阵来达到目的。
单位矩阵
可以理解为常量中的1,任何矩阵乘于单位矩阵都不变。
逆矩阵
逆矩阵可以理解为倒数,即当前矩阵乘于其逆矩阵的结果为单位矩阵,需要注意的是,只有方阵(行列数量相等)才有逆矩阵,同时不是所有的方阵都有逆矩阵。
引入逆矩阵的原因之一是用来实现矩阵的除法。比如有矩阵X,A,B,其中X*A = B,我们要求X矩阵的值。本能来说,我们只需要将B/A就可以得到X矩阵了。但是对于矩阵来说,不存在直接相除的概念。我们需要借助逆矩阵,间接实现矩阵的除法。具体的做法是等式两边在相同位置同时乘以矩阵A的逆矩阵,如下所示,X*A*(A的逆矩阵)=B*(A的逆矩阵)。由于A*(A的逆矩阵)=I,即单位矩阵,任何矩阵乘以单位矩阵的结果都是其本身。所以,我们可以得到X=B*(A的逆矩阵)。
转置矩阵
转置矩阵是指将行列互换之后的矩阵,和逆矩阵常用于法线变换。
仿射变换
矩阵的仿射变换包含了主要包含了平移、旋转和缩放。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号