第十七天学习进度--规律寻找算法之算法统一（3）

前几天的多项式和幂次指数函数曲线函数拟合算法虽然各自都能够拟合很多种情况的曲线，而且之间有相通之处，但不可否认之处，二者在拟合曲线的时候还是都有各自单独拟合函数的情况，也就是说，如果没有把多项式函数拟合和幂函数指数函数拟合的两个算法统一起来的话，这样的时候能够拟合曲线的范围并不像两者统一起来的时候这么广泛，为了让前几天函数拟合曲线的范围更加广泛，也就是更加智能，所以有必要再写一个章节将二者统一

因此为了解决究竟是哪种情况更适用哪种情况的拟合，有必要假如对应的决策分析。所以大前天写的博客：相关系数和显著水平

这篇博文中的相关系数和显著水平成了评测哪一种预测效果更佳的决策参数，在此分析的基础上，对前几天的多项式函数拟合算法和幂函数指数函数的函数拟合多增加一个返回 相关系数*(1-显著水平) 的参数来评估对应的曲线对于函数拟合究竟是哪一种方式拥有更加好的效果。

然后我们编写出以下的统一二者的函数，其中funcmodel是多项式拟合的算法，funcmodel2是指数函数幂函数拟合的算法

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# @Time  : 2020/7/25 18:55
# @Author: hdq
# @File  : myfunctool.py

# 将会有更精准的拟合效果,但是载入速度更慢

from tools import funcmodel as func1
from tools import funcmodel2  as func2

#selectmode:1 func1,2 fucn2,3 func1 or func2
def find_logical(y, inpercent=100, limitfunc=lambda x: x ** 3,selectmode=3):
    fit_coef, alist, x, score=None,None,None,None
    fit_coef2, x2, func, score2=None,None,None,None
    if selectmode==3:
        fit_coef, alist, x, score = func1.auto_find_logical(y, inpercent)
        fit_coef2, x2, func, score2 = func2.find_logical(y, limitfunc)
    elif selectmode==2:
        fit_coef2, x2, func, score2 = func2.find_logical(y, limitfunc)
    elif selectmode==1:
        fit_coef, alist, x, score = func1.auto_find_logical(y, inpercent)

    if selectmode==1 or (selectmode == 3 and score > score2):
        return 1, fit_coef, alist,score, x
    else:
        return 2, fit_coef2, func,score2, x2


def func_general(info, x):
    if info[0] == 1:
        return func1.func_general(info[1], x)
    else:
        return info[2](x, *info[1])


def auto_func(x, y, inpercent=100, limitfunc=lambda x: x ** 3,selectmode=3):
    fit_coef, alist, score = None, None, None
    fit_coef2, func, score2 = None, None, None
    if selectmode == 3:
        fit_coef, alist, score = func1.auto_ax_bfit(x, y, inpercent)
        fit_coef2, func, score2 = func2.polyfit(x, y, limitfunc)
    elif selectmode == 2:
        fit_coef2, func, score2 = func2.polyfit(x, y, limitfunc)
    elif selectmode == 1:
        fit_coef, alist, score = func1.auto_ax_bfit(x, y, inpercent)
    if selectmode==1 or (selectmode == 3 and score > score2):
        return 1, fit_coef, alist,score, x
    else:
        return 2, fit_coef2, func,score2, x


# 展示函数图像
def show_func(info, x_min, x_max, exactvalue=201):
    if info[0] == 1:
        func1.show_func(info[1], x_min, x_max, exactvalue)
    else:
        func2.show_func(info[1], info[2], x_min, x_max, exactvalue)


# 得到函数公式
def get_func(info):
    result = "F(x)="
    if info[0] == 1:
        lennum = len(info[1])
        for i in range(lennum):
            if i == 0:
                result += "("+str(info[1][i])+")"
            else:
                result += "+("+str(info[1][i])+")"
            if (lennum - i) > 1:
                result += "X^%d" % (lennum - i)
            elif i == (lennum - 2):
                result += "X"
    else:
        if info[2].__name__ == "func_exxaxx":
            result += "(%e)*e^(%e)X+(%e)X^(%e)+(%e)X^(%e)X+(%e)" % (
                info[1][0], info[1][1], info[1][2], info[1][3], info[1][4], info[1][5], info[1][6])
        elif info[2].__name__ == "func_exxa":
            result += "(%e)*e^(%e)X+(%e)X^(%e)+(%e)" % (info[1][0], info[1][1], info[1][2], info[1][3], info[1][4])
        elif info[2].__name__ == "func_exxx":
            result += "(%e)*e^(%e)X+(%e)X^(%e)X+(%e)" % (info[1][0], info[1][1], info[1][2], info[1][3], info[1][4])
        elif info[2].__name__ == "func_xaxx":
            result += "(%e)X^(%e)+(%e)X^(%e)X+(%e)" % (info[1][0], info[1][1], info[1][2], info[1][3], info[1][4])
        elif info[2].__name__ == "func_ex":
            result += "(%e)*e^(%e)X+(%e)" % (info[1][0], info[1][1], info[1][2])
        elif info[2].__name__ == "func_xa":
            result += "(%e)X^(%e)+(%e)" % (info[1][0], info[1][1], info[1][2])
        elif info[2].__name__ == "func_xx":
            result += "(%e)X^(%e)X+(%e)" % (info[1][0], info[1][1], info[1][2])
    return result

 

对于一个每次增加2^n的数列

[1,3,7,15,31,63]

预测他的下一个数,正确答案是127

#规律寻找
info=find_logical([1,3,7,15,31,63])
print(func_general(info,[info[-1][-1]+1]))

 

看看结果：

 

 

 

 

对于输入斐波那契数列，展示他的前20个数函数走势

# 图像展示
info = find_logical([1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765])
show_func(info, 1, 20)

斐波那契数列函数拟合结果如下

 

 

 

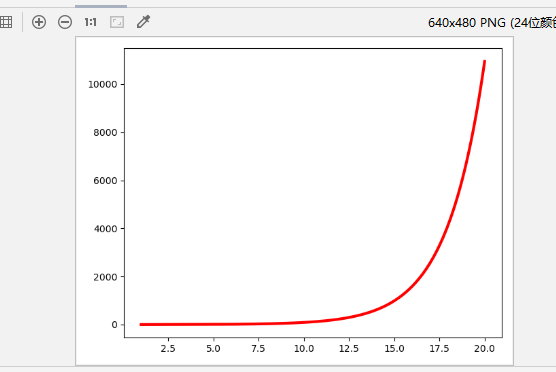
接下来拟合斐波那契数列，并预测他的下一个数值，通过前几天的学习我们知道斐波那契数列的下一个数值是10946

#曲线匹配
x=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]
y=[1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765]
info=auto_func(x,y)
print(func_general(info,[info[-1][-1]+1]))

看看预测结果：

 

 

 

接下来如果通过输入一个数列，如何得到他的拟合函数表达式

数列

[1,11,111,1111,11111,111111]

# 获得曲线表示函数(selectmode 设置特定函数)
info = find_logical([1,11,111,1111,11111,111111])
print("下一个值",func_general(info,[info[-1][-1]+1]))
print(get_func(info))