第十四天学习进度--相关系数和显著水平

昨天学习到曲线拟合的python实现方式，今天，就是根据提供的数据，然后获得对应数据线性相关程度的表示量，以此来获得两组数据间的关联程度

相关系数R是研究数据之间线性相关程度的量，就是说一组数据的改变会不会有某种原因导致另外一组数据的改变之间的相关程度。当相关系数在0.7以上就说明两组数据之间的关系非常紧密，0.4-0.7则是说明关系紧密，0.2-0.4说明的是关系一般，以下的话说明两组数据之间的基本不相关。

而相关系数并不是决定两组关系之间唯一的量，因为即使是两组数据之间的数据的关系紧密，也有可能是由于偶然而引起的关系紧密。这个时候就要用到另外一个量，显著水平（P值），来说明两组数据之间的关系之间的偶然关系程度的强弱。

显著系数的值是说明两组数据之间的关系之间的偶然关系程度的强弱，也就表示的两组数据之间的相关是不是因为偶然因素引起的。当P<0.05时表示这两组数据之间显著相关，而当P<0.01时，则表示非常显著相关。当P>0.05时，则表示两组数据间的关系很有可能是因为偶然关系导致的相关性。

用具体的例子来说明 当P=0.03，相关系数R=0.364的时候，表示的是两组数据之间显著相关（有相关关系），相关系数为0.364（简单来说相当于线性相关的程度）。

而当P=0.07时，相关系数为R=0.9时，表示的是两组数据之间的相关程度很有可能是因为偶然而导致的相关关系（无相关关系），虽然两组数据相关系数很大为0.9。

而在Python中，已经为我们提供了一个很方便的函数用来计算两组数据之间的相关程度spicy中的stats中就有方法

stats.pearsonr(a,b)

返回的是一个(相关系数,显著水平)的元组

 

有了上述的方法之后，让我们来实验一番

利用昨天我们自己想的数据作为参考，代入

函数 y=2x^3+x^2+1

分别取x=[1,2,3,4,5]

对应的y就为y=[4,21,64,145,276]

#相关系数分析
x=[1,2,3,4,5]
y=[4,21,64,145,276]
import scipy.stats as stats
print(stats.pearsonr(x,y))

结果如下

 

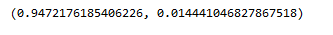
 可以看到两组关系之间的相关系数是0.947左右，也就是说相关程度非常非常大

而显著水平接近0.01左右，也就是说基本上可以看成是非常显著了，也就是说两组数据之间的关系的相关程度很大程度上不是因为偶然的因素引起的。

所以两个系数得到了之后，就基本上可以说，列表x和列表y之间基本非常显著有很大的相关程度

 

而如果修改其中的一个数值，来破坏其中的相关程度呢?我们来看看效果

将y值对应的5的值修改为0，此时y=[4,21,64,145,0]

此时数据如下

#相关系数分析
x=[1,2,3,4,5]
y=[4,21,64,145,0]
import scipy.stats as stats
print(stats.pearsonr(x,y))

实验结果

 

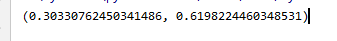
 可以看到显著水平值很大，也就是说两者间的0.3的关系基本上可以断定是因为偶然因素引起的。