基于Julia语言简单实现了ADAM优化算法

基于Julia语言实现了简单的ADAM优化算法

2023-01-28

    ADAM优化方法来自于Kingma D在2014年的一篇文章，后来广泛应用于神经网络训练中。为学习Adam也为了熟悉julia语言的操作，这里用Julia实现了Adam算法。

Kingma D ,  Ba J . Adam: A Method for Stochastic Optimization[J]. Computer Science, 2014.

1.首先是待优化的函数，这里使用一个二维的函数：

f(x)=5x²+2y²+0.1x-5y+4

它的函数图像是：

 

 

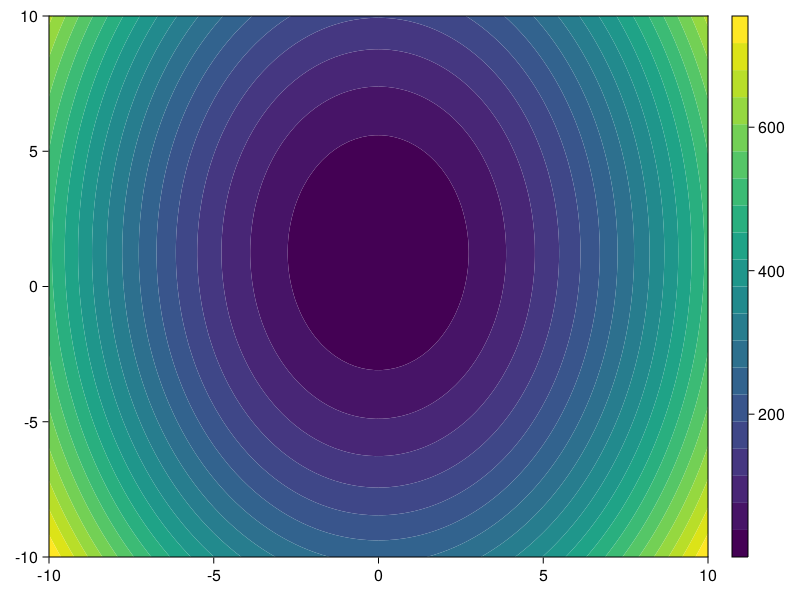
将其用代码表示：

function func(x::AbstractVector)
    val = 5*x[1]^2 + 2*x[2]^2 + 0.1*x[1] - 5*x[2] + 4
end

2.该函数的一介导函数

function grad_func(x)
    val1 = 10*x[1] + 0.1
    val2 = 4*x[2] - 5
    [val1;val2]
end

3.Adam算法实现，将其放在函数myadam里

查看代码

"""
    myadam(paranum,func,grad_func;...)
    
My ADAM methed from Kingma D,it get one input of number of parameters.

paranum:参数数目
func:优化函数
grad_func:优化函数一介导
lamb: 学习率
maxiternum:最大迭代次数
numpara:存储参数迭代的间隔

    reference:
[1] Kingma D ,  Ba J . Adam: A Method for Stochastic Optimization[J]. Computer Science, 2014.

Examples
========
    julia>max(2,5,1)
    5
"""
function myadam(paranum,func,grad_func;lamb=0.01, maxiternum=10000, numpara=10)
    ϵ = 1e-10
    gamma = 0.9
    θ = 1e-8
    β1 = 0.9
    β2 = 0.999
    
    #x0 = 1;y0 = 1
    #f1 = func(x0, y0)
    para = rand(paranum) .+ 7 #初始化参数值
    npara = copy(para')
    f1 = func(para)
    f2 = 0
    iter = 0
    mₜ = 0; vₜ = 0

    while true
        if abs(f1 - f2) < ϵ || iter > maxiternum
            break
        end
        f1 = func(para)
        #g = [grad_func_x(para);grad_func_y(para)]
        g = grad_func(para)
        mₜ = β1*mₜ .+ (1-β1)*g
        vₜ = β2*vₜ .+ (1-β2)*(g.*g)
        m_hat = mₜ/(1-β1)
        v_hat = vₜ/(1-β2)

        para = para .- lamb ./ (θ .+ sqrt.(v_hat)) .* m_hat
        f2 = func(para)
        if iter % numpara == 0
            npara = vcat(npara,para')
        end
        iter += 1
    end
    println("The best solution is:", f2)
    println("now the parameter is:", para)
    println("number of iter is:", iter)
    f2, para, iter, npara
end

4.使用函数func来进行测试

查看代码

using CairoMakie
f2, para, iter, npara = myadam(2,func,grad_func)
#
xs = LinRange(-10, 10, 100)
ys = LinRange(-10, 10, 100)
x = [xs ys]'
y = func(x)
fig = Figure()
ax1 = Axis(fig[1,1])
co = contourf!(xs,ys,y,levels = 20)
scatterlines!(npara[:,1],npara[:,2],color = :skyblue)
Colorbar(fig[1,2], co)
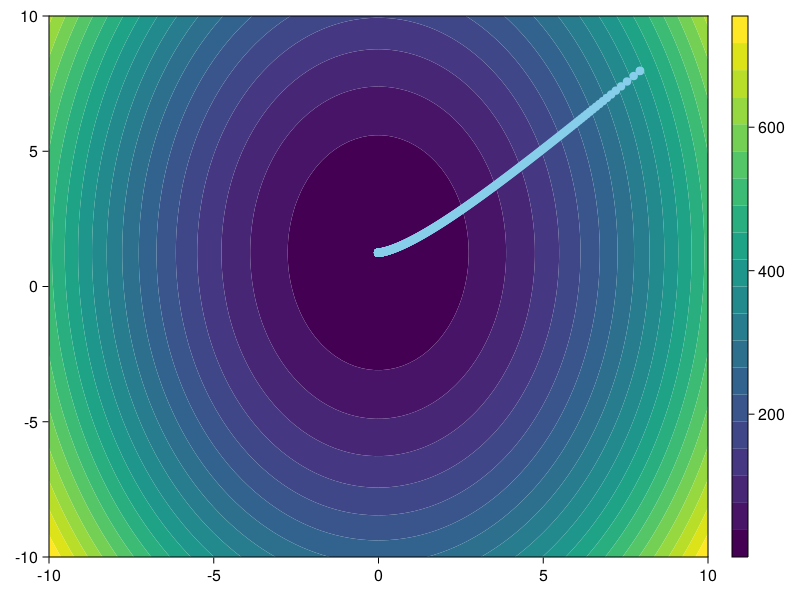
fig

5.结果展示

The best solution is:0.8745000076080198
now the parameter is:[-0.009960992354842862, 1.2500001378197478]
number of iter is:5184