吴恩达深度学习第二课第一周编程作业_Initialization（初始化）

Initialization（初始化）

本文作业是在jupyter notebook上一步一步做的，带有一些过程中查找的资料等（出处已标明）并翻译成了中文，如有错误，欢迎指正！

欢迎来到“改进深度神经网络”的第一个作业。

训练神经网络需要指定权重的初始值。一个精心选择的初始化方法将有助于学习。

如果您完成了这个专门化的前一门课程，那么您可能按照我们的说明进行了权重初始化，到目前为止，它已经完成了。但是如何选择一个新的神经网络的初始化呢?在这个笔记本中，您将看到不同的初始化如何导致不同的结果。

一个精心选择的初始化可以:
•加速梯度下降的收敛
•增加梯度下降收敛为较低训练(和泛化)误差的几率

首先，运行以下单元格以加载包和您将尝试分类的平面数据集。

import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from init_utils import sigmoid, relu, compute_loss, forward_propagation, backward_propagation
from init_utils import update_parameters, predict, load_dataset, plot_decision_boundary, predict_dec

%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots 设置图形的默认大小
plt.rcParams['image.interpolation'] = 'nearest'#设置插值为最近的
plt.rcParams['image.cmap'] = 'gray' #设置颜色样式

# load image dataset: blue/red dots in circles 加载图像数据集:蓝色/红色圆点在圆圈
train_X, train_Y, test_X, test_Y = load_dataset()

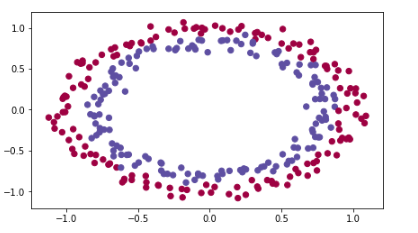
您需要一个分类器来区分蓝点和红点。

　　Scikit-learn(sklearn)是机器学习中常用的第三方模块，对常用的机器学习方法进行了封装，包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)、聚类　　(Clustering)等方法。

　　Python之Sklearn使用教程，来自爱折腾的大懒猪，链接：https://www.jianshu.com/p/6ada34655862

1 - Neural Network model 神经网络模型

您将使用一个3层神经网络(已经为您实现了)。这里是你将试验的初始化方法:
•zero初始化——设置初始化=“zero”在输入参数中。
•随机初始化——在输入参数中设置初始化=“Random”。这会将权重初始化为较大的随机值。
•He初始化——设置初始化=输入参数中的“He”。这将根据He等人2015年的一篇论文将权重初始化为按比例缩放的随机值。

说明:请快速阅读下面的代码，并运行它。在下一部分中，您将实现这个模型()调用的三个初始化方法。

 1 def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he"):
 2     """
 3     Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
 4     
 5     Arguments:
 6     X -- input data, of shape (2, number of examples) 输入数据，形状为（2, 样本数）
 7     Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples) 真是标签向量（0为红点，1为蓝点），形状（1, y样本数）
 8     learning_rate -- learning rate for gradient descent 梯度下降的学习率
 9     num_iterations -- number of iterations to run gradient descent 运行梯度下降的迭代次数
10     print_cost -- if True, print the cost every 1000 iterations如果为真，每1000次迭代打印成本
11     initialization -- flag to choose which initialization to use ("zeros","random" or "he")
12     
13     Returns:
14     parameters -- parameters learnt by the model 模型学习的参数
15     """
16         
17     grads = {}
18     costs = [] # to keep track of the loss 记录损失情况
19     m = X.shape[1] # number of examples 样本数量
20     layers_dims = [X.shape[0], 10, 5, 1] #每层的神经单元数，分别是第0层，第一层
21     
22     # Initialize parameters dictionary.初始化参数字典，如下：有三种方式
23     if initialization == "zeros":
24         parameters = initialize_parameters_zeros(layers_dims)
25     elif initialization == "random":
26         parameters = initialize_parameters_random(layers_dims)
27     elif initialization == "he":
28         parameters = initialize_parameters_he(layers_dims)
29 
30     # Loop (gradient descent)循环，梯度下降
31 
32     for i in range(0, num_iterations):
33 
34         # Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
35         a3, cache = forward_propagation(X, parameters)
36         
37         # Loss损失
38         cost = compute_loss(a3, Y)
39 
40         # Backward propagation.反向传播 
41         grads = backward_propagation(X, Y, cache)
42         
43         # Update parameters.更新参数
44         parameters = update_parameters(parameters, grads, learning_rate)
45         
46         # Print the loss every 1000 iterations
47         if print_cost and i % 1000 == 0:
48             print("Cost after iteration {}: {}".format(i, cost))
49             costs.append(cost)
50             
51     # plot the loss
52     plt.plot(costs)
53     plt.ylabel('cost')
54     plt.xlabel('iterations (per hundreds)')
55     plt.title("Learning rate =" + str(learning_rate))
56     plt.show()
57     
58     return parameters

2 - Zero initialization 零初始化

在神经网络中有两种类型的参数需要初始化:

•权重矩阵(W^[1]，W^[2]，W^[3]，…)，W ^[L−1]，W^[L])
•偏差向量(b^[1]，b^[2]，b^[3]，…)，b^[L−1]，b^[L])

练习:实现以下函数，将所有参数初始化为零。稍后您将看到，这并不能很好地工作，因为它不能“破坏对称”，但让我们无论如何尝试一下，看看会发生什么。使用np. 0((..，..))和正确的形状。

 1 # GRADED FUNCTION: initialize_parameters_zeros 
 2 
 3 def initialize_parameters_zeros(layers_dims):
 4     """
 5     Arguments:
 6     layer_dims -- python array (list) containing the size of each layer. python数组(列表)，包含每一层的大小。
 7     
 8     Returns:
 9     parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
10                     W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
11                     b1 -- bias vector of shape (layers_dims[1], 1)
12                     ...
13                     WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
14                     bL -- bias vector of shape (layers_dims[L], 1)
15     """
16     
17     parameters = {}
18     L = len(layers_dims)            # number of layers in the network 网络的层数
19     
20     for l in range(1, L):
21         ### START CODE HERE ### (≈ 2 lines of code)
22         parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l - 1]))
23         parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
24         ### END CODE HERE ###
25     return parameters

# GRADED FUNCTION: initialize_parameters_zeros

parameters = initialize_parameters_zeros([3,2,1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

结果：

运行以下代码，使用零初始化对模型进行15,000次迭代。

parameters = model(train_X, train_Y, initialization = "zeros")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

结果：

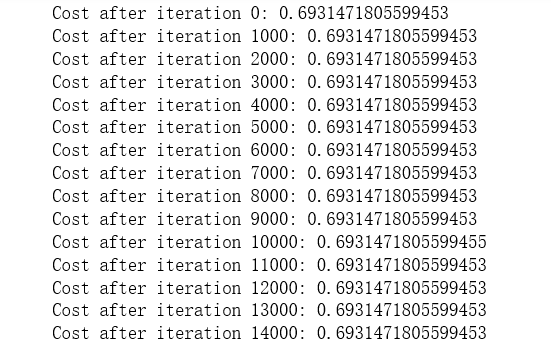
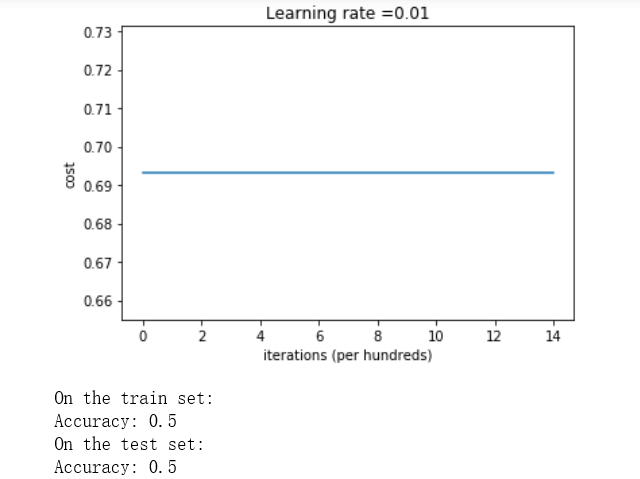
性能是非常糟糕的,并不真正降低成本,算法的表现没有比随机猜测更好。为什么?让我们看看预测和决策边界的细节:

print ("predictions_train = " + str(predictions_train))
print ("predictions_test = " + str(predictions_test))

plt.title("Model with Zeros initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

这儿会出现错误，还是由于数组维度的问题：

 1 TypeError                                 Traceback (most recent call last)
 2 D:\ProgramData\Anaconda3\lib\site-packages\matplotlib\colors.py in to_rgba(c, alpha)
 3     165     try:
 4 --> 166         rgba = _colors_full_map.cache[c, alpha]
 5     167     except (KeyError, TypeError):  # Not in cache, or unhashable.
 6 
 7 TypeError: unhashable type: 'numpy.ndarray'
 8 
 9 During handling of the above exception, another exception occurred:
10 
11 ValueError                                Traceback (most recent call last)
12 D:\ProgramData\Anaconda3\lib\site-packages\matplotlib\axes\_axes.py in scatter(self, x, y, s, c, marker, cmap, norm, vmin, vmax, alpha, linewidths, verts, edgecolors, **kwargs)
13    4287                 # must be acceptable as PathCollection facecolors
14 -> 4288                 colors = mcolors.to_rgba_array(c)
15    4289             except ValueError:
16 
17 D:\ProgramData\Anaconda3\lib\site-packages\matplotlib\colors.py in to_rgba_array(c, alpha)
18     266     for i, cc in enumerate(c):
19 --> 267         result[i] = to_rgba(cc, alpha)
20     268     return result
21 
22 D:\ProgramData\Anaconda3\lib\site-packages\matplotlib\colors.py in to_rgba(c, alpha)
23     167     except (KeyError, TypeError):  # Not in cache, or unhashable.
24 --> 168         rgba = _to_rgba_no_colorcycle(c, alpha)
25     169         try:
26 
27 D:\ProgramData\Anaconda3\lib\site-packages\matplotlib\colors.py in _to_rgba_no_colorcycle(c, alpha)
28     222     if len(c) not in [3, 4]:
29 --> 223         raise ValueError("RGBA sequence should have length 3 or 4")
30     224     if len(c) == 3 and alpha is None:
31 
32 ValueError: RGBA sequence should have length 3 or 4
33 
34 During handling of the above exception, another exception occurred:
35 
36 ValueError                                Traceback (most recent call last)
37 <ipython-input-12-0ec6f7c907fb> in <module>()
38       3 axes.set_xlim([-1.5,1.5])
39       4 axes.set_ylim([-1.5,1.5])
40 ----> 5 plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
41 
42 ~\Downloads\代码作业\第二课第一周编程作业\assignment1\init_utils.py in plot_decision_boundary(model, X, y)
43     215     plt.ylabel('x2')
44     216     plt.xlabel('x1')
45 --> 217     plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
46     218     plt.show()
47     219 
48 
49 D:\ProgramData\Anaconda3\lib\site-packages\matplotlib\pyplot.py in scatter(x, y, s, c, marker, cmap, norm, vmin, vmax, alpha, linewidths, verts, edgecolors, hold, data, **kwargs)
50    3473                          vmin=vmin, vmax=vmax, alpha=alpha,
51    3474                          linewidths=linewidths, verts=verts,
52 -> 3475                          edgecolors=edgecolors, data=data, **kwargs)
53    3476     finally:
54    3477         ax._hold = washold
55 
56 D:\ProgramData\Anaconda3\lib\site-packages\matplotlib\__init__.py in inner(ax, *args, **kwargs)
57    1865                         "the Matplotlib list!)" % (label_namer, func.__name__),
58    1866                         RuntimeWarning, stacklevel=2)
59 -> 1867             return func(ax, *args, **kwargs)
60    1868 
61    1869         inner.__doc__ = _add_data_doc(inner.__doc__,
62 
63 D:\ProgramData\Anaconda3\lib\site-packages\matplotlib\axes\_axes.py in scatter(self, x, y, s, c, marker, cmap, norm, vmin, vmax, alpha, linewidths, verts, edgecolors, **kwargs)
64    4291                 raise ValueError("c of shape {} not acceptable as a color "
65    4292                                  "sequence for x with size {}, y with size {}"
66 -> 4293                                  .format(c.shape, x.size, y.size))
67    4294         else:
68    4295             colors = None  # use cmap, norm after collection is created
69 
70 ValueError: c of shape (1, 300) not acceptable as a color sequence for x with size 300, y with size 300

错误情况

解决办法：参考自：十一点三十六，链接：https://blog.csdn.net/qq_33782064/article/details/80259141

结果：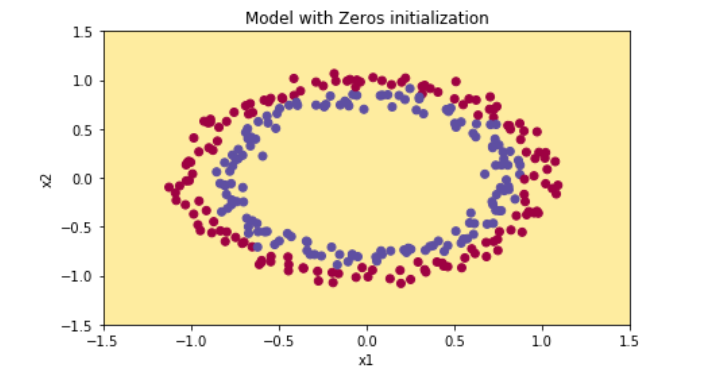

模型对每个例子的预测都是0。

一般来说，将所有权值初始化为零会导致网络无法破坏对称性。这意味着每一层中的每一个神经元都将学习相同的东西，你也可以用n^[l] =1来训练一个神经网络，而这个网络并不比线性分类器(比如logistic回归)更强大。

**你应该记住的**：-权重W^[l]应该被随机初始化以打破对称性。-然而，将偏差b^[l]初始化为零是可以的。随机初始化W^[l]仍然破坏了对称性。

3 - Random initialization 随机初始化

为了打破对称性，让权重随机化。在随机初始化之后，每个神经元可以继续学习其输入的不同函数。在这个练习中，您将看到如果权重被随机地初始化，但是权重是非常大的值会发生什么。

练习：执行以下函数，将权重初始化为大的随机值(按*10的比例缩放)，并将偏差初始化为零。为了偏见，使用np.random.randn(..，..) * 10来表示权重和np. 0 (..)。我们使用固定的np.random.seed(..)来确保您的“随机”权重与我们的匹配，所以如果运行几次您的代码总是给您相同的参数初始值，也不用担心。

 1 # GRADED FUNCTION: initialize_parameters_random
 2 
 3 def initialize_parameters_random(layers_dims):
 4     """
 5     Arguments:
 6     layer_dims -- python array (list) containing the size of each layer.
 7     
 8     Returns:
 9     parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
10                     W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
11                     b1 -- bias vector of shape (layers_dims[1], 1)
12                     ...
13                     WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
14                     bL -- bias vector of shape (layers_dims[L], 1)
15     """
16     
17     np.random.seed(3)               # This seed makes sure your "random" numbers will be the as ours
18     parameters = {}
19     L = len(layers_dims)            # integer representing the number of layers
20     
21     for l in range(1, L):
22         ### START CODE HERE ### (≈ 2 lines of code)
23         parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * 10
24         parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
25         ### END CODE HERE ###
26 
27     return parameters

# GRADED FUNCTION: initialize_parameters_random

parameters = initialize_parameters_random([3, 2, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

结果：

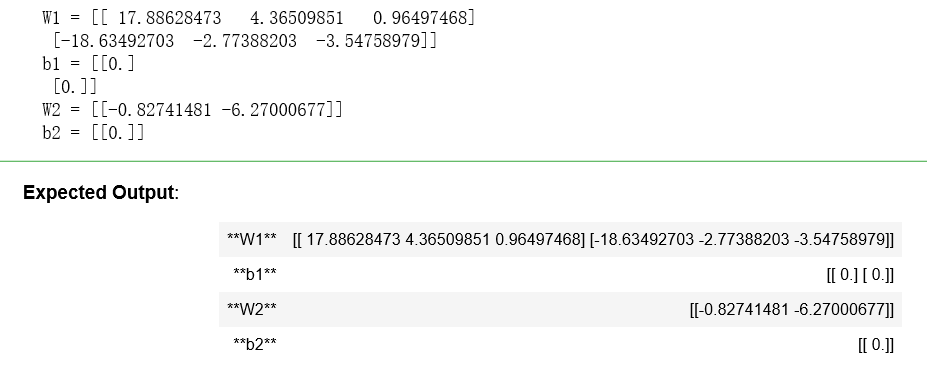
运行以下代码，使用随机初始化对模型进行15,000次迭代训练。

parameters = model(train_X, train_Y, initialization = "random")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

结果：

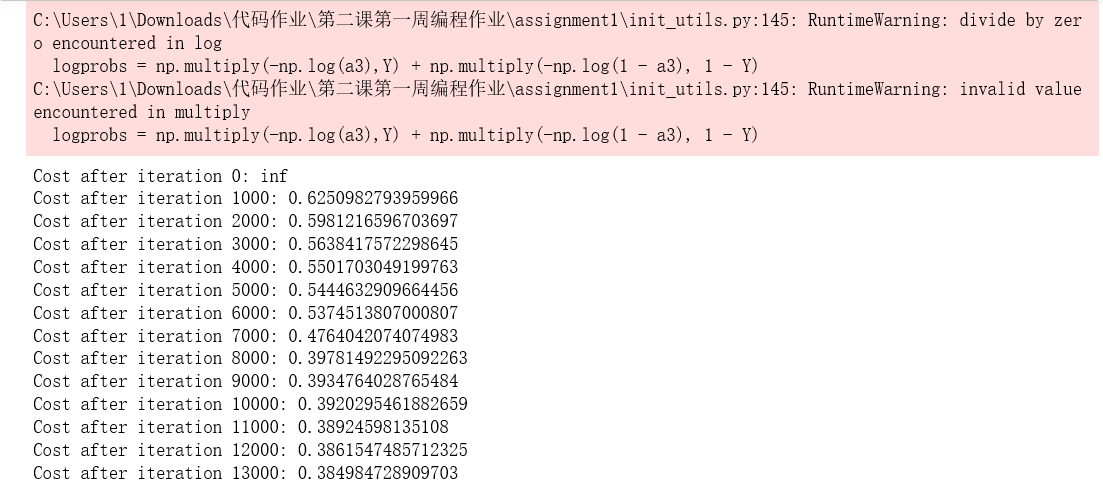
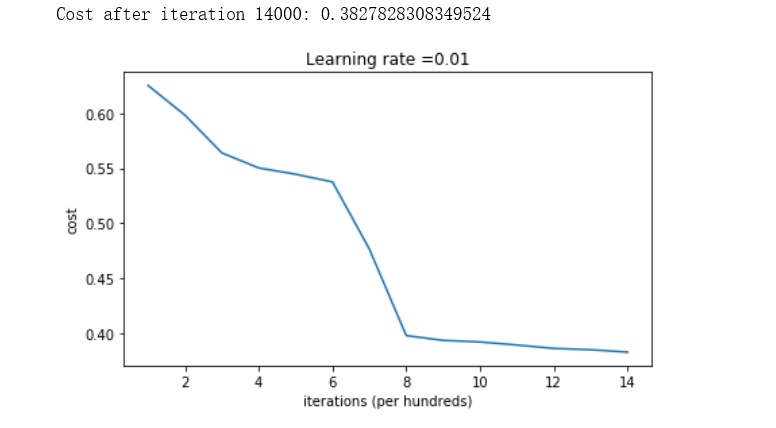
神经网络中的RuntimeWarning: divide by zero encountered in log问题，参考：BUB1997

如果你看到“inf”是迭代0之后的代价，这是因为数值舍入;一个更复杂的数字实现可以解决这个问题。但就我们的目的而言，这并不值得担心。
不管怎么说，看起来你破坏了对称性，这就得到了更好的结果。比以前。模型不再输出所有0。

print (predictions_train)
print (predictions_test)

plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

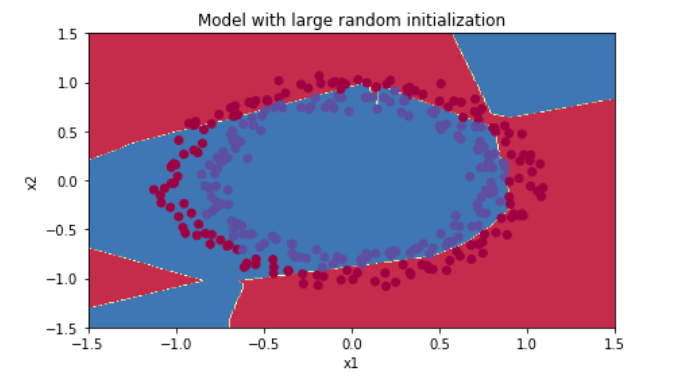
观察：
•成本一开始就很高。这是因为对于大型随机值权重，最后一个激活(sigmoid)在某些示例中输出的结果非常接近于0或1，而当它错误地执行该示例时，会对该示例造成非常大的损失。确实，当log(a^[3])=log(0)时，损失趋于无穷。
•糟糕的初始化会导致梯度消失/爆炸，这也会减慢优化算法。
•如果你训练这个网络的时间更长，你会看到更好的结果，但初始化过大的随机数会降低优化速度。
-将权重初始化为非常大的随机值并不能很好地工作。希望用小的随机值初始化效果更好。重要的问题是:这些随机值应该有多小?让我们在下一部分中揭晓答案!

4 - He initialization He初始化

最后，尝试“He初始化”；以He et al.， 2015的第一作者命名。(如果您听说过“Xavier初始化”，这与此类似，除了Xavier初始化为sqrt(1./layers_dims[l-1])的权重W^[l]使用一个比例因子，其中初始化将使用sqrt(2./layers_dims[l-1])。)

练习:实现以下函数来初始化参数。

提示：这个函数类似于前面的initialize_parameters_random(…)。唯一的区别是，不是将np.random.randn(..，..)乘以10，而是将其乘以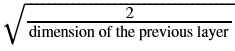

，这是他对ReLU激活的层的初始化建议。

 1 # GRADED FUNCTION: initialize_parameters_he
 2 
 3 def initialize_parameters_he(layers_dims):
 4     """
 5     Arguments:
 6     layer_dims -- python array (list) containing the size of each layer.
 7     
 8     Returns:
 9     parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
10                     W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
11                     b1 -- bias vector of shape (layers_dims[1], 1)
12                     ...
13                     WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
14                     bL -- bias vector of shape (layers_dims[L], 1)
15     """
16     
17     np.random.seed(3)
18     parameters = {}
19     L = len(layers_dims) - 1 # integer representing the number of layers
20      
21     for l in range(1, L + 1):
22         ### START CODE HERE ### (≈ 2 lines of code)
23         parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * np.sqrt(2. / layers_dims[l-1])
24         parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
25         ### END CODE HERE ###
26         
27     return parameters

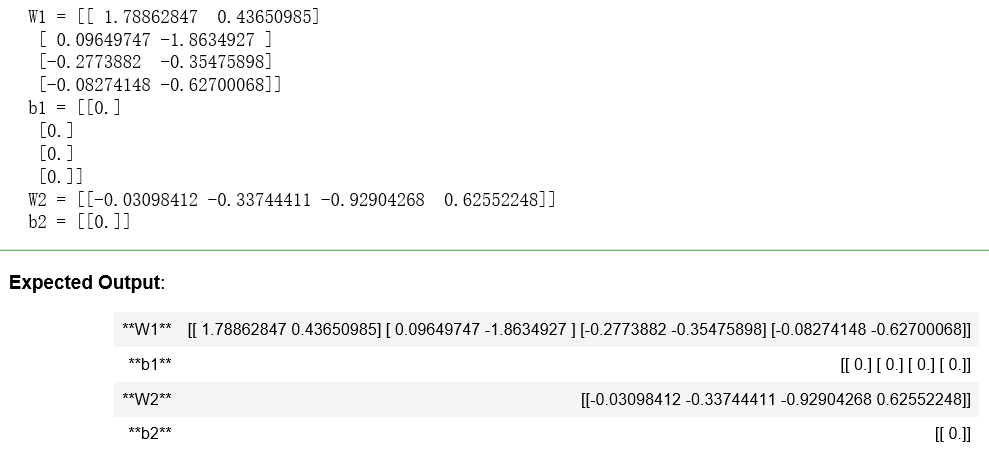
# GRADED FUNCTION: initialize_parameters_he

parameters = initialize_parameters_he([2, 4, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

结果：

运行以下代码，使用He初始化对模型进行15,000次迭代训练。

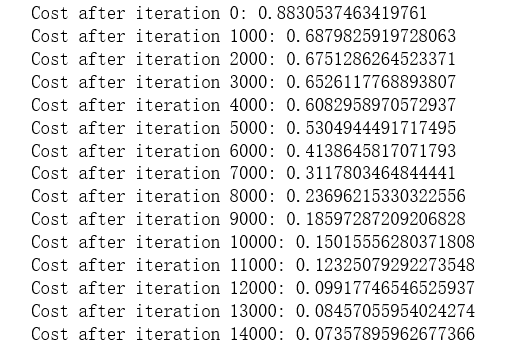
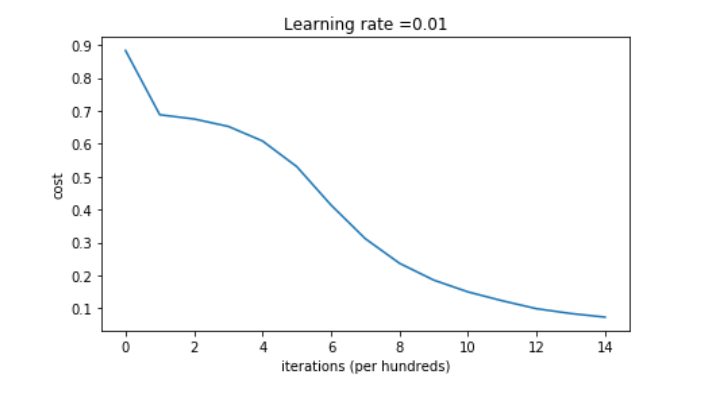
parameters = model(train_X, train_Y, initialization = "he")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

plt.title("Model with He initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

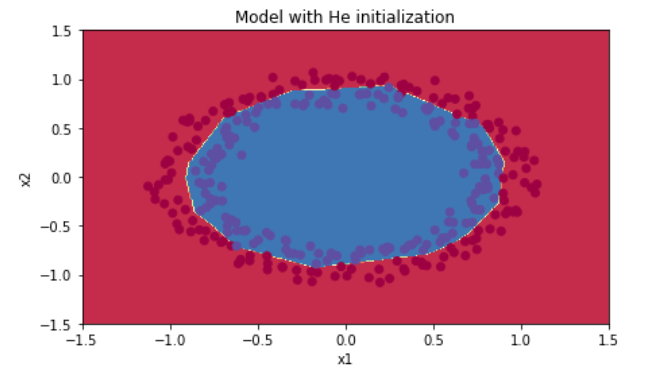
观察：
•具有He初始化的模型在少量的迭代中很好地分离了蓝色和红色的点。

5 - Conclusions 结论

</tr>
    <td>
    3-layer NN with zeros initialization
    </td>
    <td>
    50%
    </td>
    <td>
    fails to break symmetry
    </td>
<tr>
    <td>
    3-layer NN with large random initialization
    </td>
    <td>
    83%
    </td>
    <td>
    too large weights 
    </td>
</tr>
<tr>
    <td>
    3-layer NN with He initialization
    </td>
    <td>
    99%
    </td>
    <td>
    recommended method
    </td>
</tr>

这里单元格内是上面这串代码，但是运行了无法显示为表格，还未找到解决办法。

* *你应该从这个笔记本记得* *：

——不同的初始化导致不同的结果

——随机初始化用于打破对称,确保不同的隐藏单元可以学到不同的东西

——不要intialize值太大——他用ReLU激活初始化适用于网络。

posted @ 2020-07-29 10:26 廖海清阅读(1231) 评论(0) 编辑收藏举报

刷新页面返回顶部

Agiroy_70's Blog

吴恩达深度学习第二课第一周编程作业_Initialization（初始化）

Initialization（初始化）

1 - Neural Network model 神经网络模型

2 - Zero initialization 零初始化

3 - Random initialization 随机初始化

4 - He initialization He初始化

5 - Conclusions 结论

公告

Agiroy_70's Blog

吴恩达深度学习 第二课第一周编程作业_Initialization（初始化）

Initialization（初始化）

1 - Neural Network model 神经网络模型

2 - Zero initialization 零初始化

3 - Random initialization 随机初始化

4 - He initialization He初始化

5 - Conclusions 结论

公告

吴恩达深度学习第二课第一周编程作业_Initialization（初始化）