算法 -- 寻找两个正序数组的中位数（二分查找）
原题：
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1：
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2
示例 2：
输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
提示：
nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106
解答：
- 如果不考虑时间复杂度这个要求的话，直接归并数组，然后求中位数就行了 ----- 以下有两个思路
- 创新数组，双指针指向两个数组，哪个小放哪个进新数组，最后奇数return 新数组res[(length-1)/2]，偶数return (res[(length-1)/2]+res[length/2])/2.0
小提升 ： 可以只循环（m+n)/2次，减少一丢丢时间复杂度 - 不用创新数组，毕竟最后只需要返回中位数就行了，我们创两个变量，一个left，一个right，存储最终计算所需的两个数据，每次遍历时将上一步right的值赋给left，后面思路同第一个方法，只是把上面存储到新数组，换成改变right变量，最后两个数据相加再减半就好，如果是奇数，left与right值相等
- 重点来咯，如果按照上面两个解法，时间复杂度为O（（m+n）/2），明显不符合题意的O（log（m+n）），若想达到这种复杂度，无疑要使用二分查找
假设我们要找第 7 小的数字。
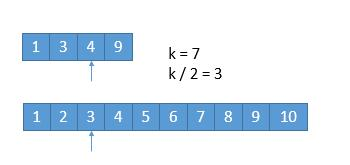
要找第7小的数字，由于两个数组都由从小到大排序，所以我们只需要递归找出两个数组中各自第k/2小的数字，再相互比较，数字小的则将其前面的数字（包括自己）删去，修改起始位置为当前数字+1，k改为k-删去数字数量
橙色的部分表示已经去掉的数字。
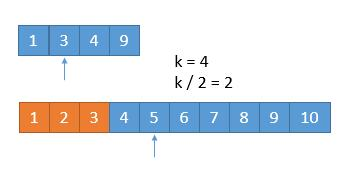
按照上面方法，排除了下排数组中的前三个数字[1,2,3]，k改为了4，即继续递归找各数组中第k/2 = 2的数字，3比5小，所以删去上排数组中的[1,3]
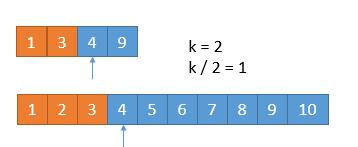
同上
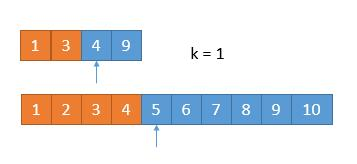
通过操作，k值来到了1，只需比较两排数组起始位置的数字即可，返回小的
所以第 7 小的数字是 4。
本题重点（边界，特殊值判断）
我们每次都是取 k/2 的数进行比较，有时候可能会遇到数组长度小于 k/2的时候。
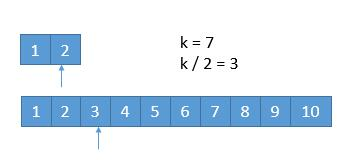
由于k/2 = 3大于了上排数组的总长度2，所以在判断数字前要先判断长度，若存在上图情况，将尾指针指向末尾就好
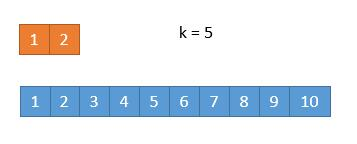
上图情况为某一排数组已经被删完了，即len1 = 0，我们该怎么办，非常好办，剩下k为多少，直接用另一个数组不就好了吗，记得加完k后要减1噢
上面图片 作者：windliang 链接：https://leetcode.cn/problems/median-of-two-sorted-arrays/solutions/8999/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-2/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
下面是我自己看完半抄半打的代码
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int m = nums1.length,n = nums2.length;
int left = (m+n+1)/2;
int right = (m+n+2)/2;
return (getK(nums1,0,m-1,nums2,0,n-1,left)+getK(nums1,0,m-1,nums2,0,n-1,right))/2.0;
}
private int getK(int[] nums1,int start1,int end1,int[] nums2,int start2,int end2,int k){
int len1 = end1-start1+1;
int len2 = end2-start2+1;
if(len1>len2)return getK(nums2,start2,end2,nums1,start1,end1,k);
if(len1 == 0)return nums2[start2+k-1];
if(k==1)return Math.min(nums1[start1],nums2[start2]);
int i = start1+ Math.min(len1,k/2)-1;
int j = start2+ Math.min(len2,k/2)-1;
if(nums1[i]<nums2[j]){
return getK(nums1,i+1,end1,nums2,start2,end2,k-(i-start1+1));
}else{
return getK(nums1,start1,end1,nums2,j+1,end2,k-(j-start2+1));
}
}
}```
