优化算法系列-模拟退火算法（1）——0-1背包问题
优化算法系列之模拟退火算法（1）——0-1背包问题
1问题描述
有一个窃贼在偷窃一家商店时发现有N件商品：第i件物品价值vi元，重wi磅，其中vi、wi都是整数。他希望带走的东西越值钱越好，但他的背包小，最多只能装下W磅的东西（W为整数）。如果每件物品或被带走或被留下，小偷应该带走哪几件东西？
2解空间
设xi表示第i件物品的取舍，1代表取，0代表舍，搜索空间为n元一维数组（x1,x2,x3,.....,xn）。因而解空间的取值范围可表示为（0，0，0，....，0），（0，0，0，......，1），（0，0，0，......，1，0），......，（1,1,1,1，......，1）。
以3个物品为例，解（0,1,0）表示（不取物品0，取物品1，不取物品2）。
3问题转化
给定W>0，wi>0，vi>0，要求找出一个n元的0-1向量（x1,x2,x3,......,xn），使得所取物品价值最大且重量之和小于W。
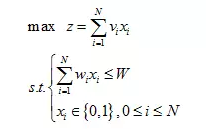
4求解结果
假设物品共10件，
其质量分别为8 12 24 16 6 9 35 21 18 19，
其价值分别为34 32 56 67 54 32 45 56 46 70，
背包能承受的最大质量为50。
根据模拟退火算法，通过MATLAB软件编程求得：
5求解代码
clc clear all close all a=0.95;%温度衰减速度 mar_length=1000;%马氏链长度 k=[34 32 56 67 54 32 45 56 46 70];%物品价值 d=[8 12 24 16 6 9 35 21 18 19];%物品重量 restriction=50;%背包能够承受的最大重量 num=length(k);%物品数量 sol_new=round(rand(1,num));%随机生成初始解 E_current=inf;E_best=inf;%E_current是当前解对应的目标函数，E_best是最优解，E_new是新解的目标函数值 t0=97;tf=3;t=t0; while t>tf for i=1:mar_length %产生随机扰动 temp1=ceil(rand*num); sol_new(1,temp1)=~sol_new(1,temp1); %检查是否满足约束 while (1) s=(sol_new*d'>restriction); if s %如果不满足约束随机放弃一个物品 temp2=find(sol_new==1); temp3=ceil(rand*length(temp2)); sol_new(temp2(temp3))=~sol_new(temp2(temp3)); else break end end %计算背包中物品的价值模拟退火算法只能求最小值，所以价值取负 E_new=sol_new*(-k'); if E_new<E_current E_current=E_new; sol_current=sol_new; if E_new<E_best E_best=E_new; sol_best=sol_new; end else if (rand<exp(-(E_new-E_current)./t)) E_current=E_new; sol_current=sol_new; else sol_new=sol_current; end end end t=t*a; end disp('最优解为') sol_best disp('物品总价值为') -E_best disp('背包中物品总重量') sol_best*d'
摘录网站：
1. https://mp.weixin.qq.com/s?__biz=MzI5OTU4NTMwNQ==&mid=2247483792&idx=1&sn=c92c179896cecc45c8efc614863e2bf9&chksm=ec951be6dbe292f0027ddc877ecd3f910df724d9b6be336e0f5b07b70c9cb55920518994ed7b&scene=21#wechat_redirect
3. https://blog.csdn.net/AI_BigData_wh/article/details/77943787?locationNum=2&fps=1
