java实现最小生成树的prim算法和kruskal算法
在边赋权图中,权值总和最小的生成树称为最小生成树。构造最小生成树有两种算法,分别是prim算法和kruskal算法。在边赋权图中,如下图所示:
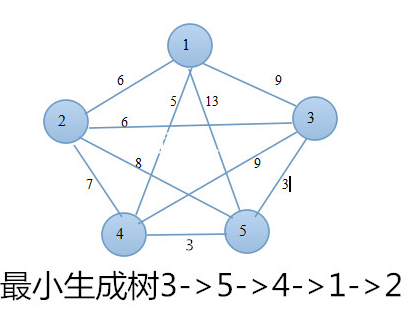
在上述赋权图中,可以看到图的顶点编号和顶点之间邻接边的权值,若要以上图来构建最小生成树。结果应该如下所示:
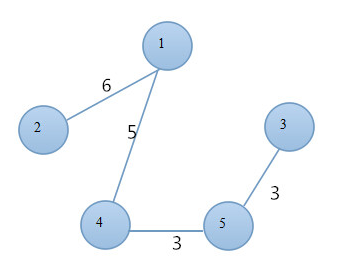
这样构建的最小生成树的权值总和最小,为17
在构建最小生成树中,一般有两种算法,prim算法和kruskal算法
在prim算法中,通过加入最小邻接边的方法来建立最小生成树算法。首先构造一个零图,在选一个初始顶点加入到新集合中,然后分别在原先的顶点集合中抽取一个顶点,使得构成的边为权值最小,然后将该笔边加入到图中,并将抽出的顶点加入到新集合中,重复这个过程,知道新集合等于原先的集合。
代码一:(java)

1 /** 2 * 最小生成树的prim算法 3 * @author liuy 4 */ 5 public class Prim { 6 7 public static void prim(int num, float[][] weight) { //num为顶点数,weight为权 8 float[] lowcost = new float[num + 1]; //到新集合的最小权 9 10 int[] closest = new int[num + 1]; //代表与s集合相连的最小权边的点 11 12 boolean[] s = new boolean[num + 1]; //s[i] == true代表i点在s集合中 13 14 s[1] = true; //将第一个点放入s集合 15 16 for(int i = 2; i <= num; i++) { //初始化辅助数组 17 lowcost[i] = weight[1][i]; 18 closest[i] = 1; 19 s[i] = false; 20 } 21 22 for(int i = 1; i < num; i++) { 23 float min = Float.MAX_VALUE; 24 int j = 1; 25 for(int k = 2; k <= num; k++) { 26 if((lowcost[k] < min) && (!s[k])) {//根据最小权加入新点 27 min = lowcost[k]; 28 j = k; 29 } 30 } 31 32 System.out.println("加入点" + j + ". " + j + "---" + closest[j]);//新加入点的j和与j相连的点 33 34 s[j] = true;//加入新点j 35 36 for(int k = 2; k <= num; k++) { 37 if((weight[j][k] < lowcost[k]) && !s[k]) {//根据新加入的点j,求得最小权 38 lowcost[k] = weight[j][k]; 39 closest[k] = j; 40 } 41 } 42 } 43 } 44 45 public static void main(String[] args) { 46 // ① 47 // / | / 48 // 6 1 5 49 // / | / 50 // ②-5--③--5--④ 51 // / // / 52 // 3 6 4 2 53 // // // 54 // ⑤--6-⑥ 55 //最小生成树为: 56 // ① 57 // | 58 // 1 59 // | 60 // ②-5--③ ④ 61 // / / / 62 // 3 4 2 63 // / // 64 // ⑤ ⑥ 65 // 66 float m = Float.MAX_VALUE; 67 float[][] weight = {{0, 0, 0, 0, 0, 0, 0}, 68 {0, m, 6, 1, 5, m, m}, 69 {0, 6, m, 5, m, 3, m}, 70 {0, 1, 5, m, 5, 6, 4}, 71 {0, 5, m, 5, m, m, 2}, 72 {0, m, 3, 6, m, m, 6}, 73 {0, m, m, 4, 2, 6, m}};//上图的矩阵 74 prim(weight.length - 1, weight); 75 //加入点3. 3---1 76 //加入点6. 6---3 77 //加入点4. 4---6 78 //加入点2. 2---3 79 //加入点5. 5---2 80 } 81 }
代码二:(java)

1 package 最小生成树; 2 /* 3 * 最小生成树prim算法,加入最小邻接边生成最小生成树。 4 * 首先构造一个零图,选择一个初始点加入到集合中, 5 * 然后分别从原来顶点的集合中抽取一个顶点, 6 * 选择的标准是构造成的树的权值最小, 7 * 循序渐进最终生成一棵最小生成树 8 */ 9 public class prim { 10 11 /* 12 * m:定义为无法到达的距离 13 * weight:邻接矩阵表,weight表示权值 14 * verNum:顶点的个数 15 * lowerW:到新集合的最小权值 16 * edge:存储到新集合的边 17 * checked:判定顶点是否被抽取的集合 18 */ 19 20 static int m=Integer.MAX_VALUE; 21 static int[][] weight={ 22 {0, 0, 0, 0, 0, 0}, 23 {0, m, 6, 9, 5, 13}, 24 {0, 6, m, 6,7,8}, 25 {0, 9,6,m,9,3}, 26 {0, 5,7,9,m,3}, 27 {0,13,8,3,3,m} 28 }; 29 static int verNum=weight.length; 30 static int []lowerW=new int[verNum]; 31 static int []edge=new int[verNum]; 32 static boolean []checked=new boolean[verNum]; 33 34 public void prim(int n,int [][]w){ 35 checked[1]=true; //抽取第一个顶点 36 37 for(int i=1;i<=n;i++){ //初始化顶点集合 38 lowerW[i]=w[1][i]; 39 edge[i]=1; 40 checked[i]=false; 41 } 42 43 for(int i=1;i<=n;i++){ 44 int min=Integer.MAX_VALUE; 45 int j=1; 46 for(int k=2;k<=n;k++){ //判定是否抽取该顶点 47 if(lowerW[k]<min&&(!checked[k])){ 48 min=lowerW[k]; 49 j=k; 50 } 51 } 52 if(i<n) //避免输出第一个顶点到第一个顶点的情况 53 System.out.println(j+"-->"+edge[j]); 54 55 checked[j]=true; //将顶点加入到新集合中 56 57 for(int k=2;k<=n;k++){ //根据新加入的顶点,求得最小的权值 58 if((w[j][k]<lowerW[k])&&(!checked[k])){ 59 lowerW[k]=weight[j][k]; 60 edge[k]=j; 61 } 62 } 63 } 64 } 65 66 public static void main(String[] args) { 67 // TODO Auto-generated method stub 68 prim p=new prim(); 69 p.prim(verNum-1,weight); 70 } 71 }
在kruskal算法中,根据边的权值以递增的方式逐渐建立最小生成树。具体操作是:将赋权图每个顶点都看做森林,然后将图中每条邻接边的权值按照升序的方式进行排列,接着从排列好的邻接边表中抽取权值最小的边,写入该边的起始顶点和结束顶点,连接顶点将森林构成树,然后读取起始结束顶点的邻接边,优先抽取权值小的邻接边,继续连接顶点将森林构成树。添加邻接边的要求是加入到图中的邻接边不构成回路。如此反复进行,直到已经添加n-1条边为止。
代码一:(java)

1 package 最小生成树; 2 import java.util.ArrayList; 3 import java.util.Scanner; 4 /* 5 * 最小生成树kruskal算法:首先将每个顶点作为一棵森林,升序比较该顶点的邻接边, 6 * 每次取最小权值的邻接边,将该邻接边连接的顶点与原先顶点构成一棵树,接着寻找 7 * 下一个顶点,继续按照邻接边权值升序进行比较,取权值最小的构成树... 8 * 9 * 该类用一个Edge类构成一个邻接边的信息,包括邻接边的起始顶点与结束顶点,权值。 10 * 用类Edge创建对象,录入对象信息,按照对象的权值进行比较,符合条件的对象加入 11 * 到链表中,最终按照链表顺序输出最小生成树。 12 */ 13 public class kruskal { 14 15 /* 16 * Max:定义顶点数组的最大值 17 * edge:链表edge,存储构造的Edge对象 18 * target:链表trget,存储最终得到结果的Edge对象 19 * parent:存储顶点信息的数组 20 * n:顶点数 21 */ 22 int Max=100; 23 ArrayList<Edge>edge=new ArrayList<Edge>(); 24 ArrayList<Edge>target=new ArrayList<Edge>(); 25 int[] parent=new int[Max]; 26 Float TheMax=Float.MAX_VALUE; 27 int n; 28 29 public void init(){ 30 /** 31 * p:起始顶点 32 * q:结束顶点 33 * w:边的权值 34 * n:顶点个数 35 */ 36 Scanner scan =new Scanner(System.in); 37 int p,q; 38 double w; 39 System.out.println("请输入结点的个数:"); 40 n=scan.nextInt(); 41 System.out.println("按照'A,B,C'的格式输入边与边的信息,ABC分别代表边的起始顶点,结束顶点,权值(输入-1 -1 -1结束输入):"); 42 while(true){ 43 p=scan.nextInt(); 44 q=scan.nextInt(); 45 w=scan.nextDouble(); 46 if(p<0||q<0||w<0)break; 47 Edge e=new Edge(); 48 e.start=p; 49 e.end=q; 50 e.weight=w; 51 edge.add(e); 52 } 53 for(int i=1;i<=n;++i){ //初始化边的信息数组 54 parent[i]=i; 55 } 56 } 57 58 /* 59 * 对象合并,将上一对象的结束边作为下一对象的起始边 60 */ 61 public void union(int j,int k){ 62 for(int i=1;i<=n;++i){ 63 if(parent[i]==j) 64 parent[i]=k; 65 } 66 } 67 68 public void kruskal(){ 69 int i=0; //顶点 70 while(i<n-1&&edge.size()>0){ //如果只有一条边或者没有边跳出 71 double min=Double.MAX_VALUE; 72 Edge temp=null; 73 for(int j=0;j<edge.size();++j){ //遍历图形 74 Edge tt=edge.get(j); 75 if(tt.weight<min){ //若两个顶点有权值,即相连 76 min=tt.weight; 77 temp=tt; 78 } 79 } 80 81 //构造一棵树 82 int jj=parent[temp.start]; 83 int kk=parent[temp.end]; 84 85 86 if(jj!=kk){ 87 ++i; //以end作为下一条边的start,寻找下一条边 88 target.add(temp); //将找到的边放入目标集合中 89 union(jj,kk); 90 } 91 edge.remove(temp); //将临时边删除 92 } 93 System.out.println("最小生成树的路径是:"); 94 for(int k=0;k<target.size();++k){ //输出最小生成树 95 Edge e=target.get(k); 96 System.out.println(e.start+"-->"+e.end); 97 } 98 } 99 100 public static void main(String[] args) { 101 // TODO Auto-generated method stub 102 kruskal kr=new kruskal(); 103 kr.init(); 104 kr.kruskal(); 105 } 106 } 107 /* 108 * start:起始顶点 109 * end:结束顶点 110 * weight:权值 111 */ 112 class Edge{ 113 public int start; 114 public int end; 115 public double weight; 116 }



