[******] 树问题:普通二叉树的创建与遍历
1. 二叉树的创建
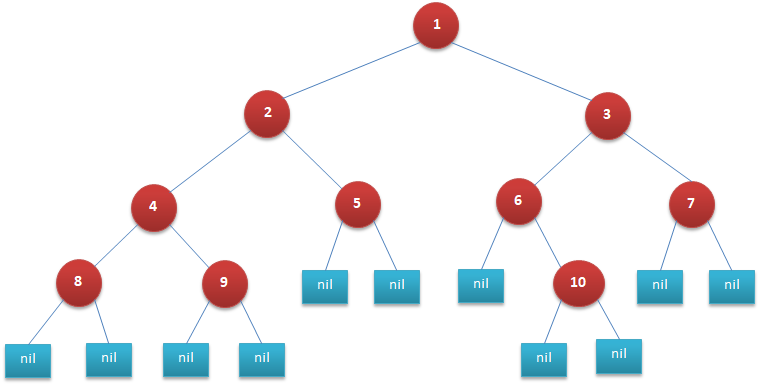
String pre_str = "1,2,4,8,-1,-1,9,-1,-1,5,-1,-1,3,6,-1,10,-1,-1,7,-1,-1";//先序输入
String post_str = "-1,-1,8,-1,-1,9,4,-1,-1,5,2,-1,-1,-1,10,6,-1,-1,7,3,1";//后序输入
String level_str = "1,2,3,4,5,6,7,8,9,-1,-1,-1,10,-1,-1";//层次输入
int[] in = {8,4,9,2,5,1,6,10,3,7}; //中序
int[] pre = {1,2,4,8,9,5,3,6,10,7}; //先序
int[] post = {8,9,4,5,2,10,6,7,3,1}; //后序
String input = "1(2(4(8,9),5),3(6(,10),7))";//括号表达式输入
static class TreeNode{ int value; TreeNode left; TreeNode right; public TreeNode(int value){ this.value = value; } }
1.1 前序遍历创建二叉树
核心思路:根左右,从左往右读
/**先序方法1*/ public static TreeNode pre_buildBTree1(InputChar ic, int flag) { int x = ic.pregetChar(); if (x == flag) return null; TreeNode t = new TreeNode(x); t.left = pre_buildBTree1(ic,flag); t.right = pre_buildBTree1(ic,flag); return t; } /**先序方法2*/ public static int position = -1; public static TreeNode pre_buildBTree2(int[] array, int flag) { int x = array[++position]; TreeNode node = null; if(position < array.length && x != flag){ node = new TreeNode(x); node.left = pre_buildBTree2(array,flag); node.right = pre_buildBTree2(array,flag); } return node; } /***用于获取值 */ static class InputChar { private int[] array; private int pos = 0; public InputChar(int[] array,int pos) { this.array = array; this.pos = pos; } public int pregetChar() { int i = pos; pos++; return array[i]; } public int postgetChar() { int i = pos; pos--; return array[i]; } } public static void main(String[] args) { /***********************先序创建二叉树***********************/ String pre_str = "1,2,4,8,-1,-1,9,-1,-1,5,-1,-1,3,6,-1,10,-1,-1,7,-1,-1";//先序 String[] array = pre_str.split(","); int [] intarray = new int[array.length]; for (int i = 0; i < intarray.length; i++) { intarray[i]=Integer.valueOf(array[i]); } //第一种先序遍历创建二叉树方法 InputChar inint = new InputChar(intarray,0); TreeNode root1 = pre_buildBTree1(inint,-1); //第二种先序遍历创建二叉树方法 position = -1; TreeNode root2 = pre_buildBTree2(intarray,-1); root1 = root2; }
1.2 后序遍历创建二叉树
核心思路:左右根,从右往左读
/**后序方法1*/ public static TreeNode post_buildBTree1(InputChar ic, int flag) { int x = ic.postgetChar(); if (x == flag) return null; TreeNode t = new TreeNode(x);//根 t.right = post_buildBTree1(ic,flag);//右 t.left = post_buildBTree1(ic,flag);//左 return t; } /**后序方法2*/ public static TreeNode post_buildBTree2(int[] array, int flag) { int x = array[--position]; TreeNode node = null; if(position >= 0 && x != flag){ node = new TreeNode(x); node.right = post_buildBTree2(array,flag); node.left = post_buildBTree2(array,flag); } return node; } /***用于获取值 */ static class InputChar { private int[] array; private int pos = 0; public InputChar(int[] array,int pos) { this.array = array; this.pos = pos; } public int pregetChar() { int i = pos; pos++; return array[i]; } public int postgetChar() { int i = pos; pos--; return array[i]; } } public static void main(String[] args) { /***********************后序创建二叉树***********************/ String post_str = "-1,-1,8,-1,-1,9,4,-1,-1,5,2,-1,-1,-1,10,6,-1,-1,7,3,1";//后序 String[] array2 = post_str.split(","); int [] intarray2 = new int[array.length]; for (int i = 0; i < intarray.length; i++) { intarray2[i]=Integer.valueOf(array2[i]); } //第一种先序遍历创建二叉树方法 InputChar inint2 = new InputChar(intarray2,intarray2.length-1); TreeNode root3 = post_buildBTree1(inint2,-1); root1 = root3; //第二种先序遍历创建二叉树方法 position = intarray2.length; TreeNode root4 = post_buildBTree2(intarray2,-1); root1 = root4; }
1.3 层次遍历创建二叉树
核心思路:利用二叉树的性质,左孩子=2*i,右孩子=2*i+1
/**层次遍历创建二叉树*/ public static TreeNode level_buildBTree(int[]array,int flag){ int len = array.length; //将数组转成list LinkedList<TreeNode> list = new LinkedList<>(); for (int i = 0; i < len; i++) { list.add(new TreeNode(array[i])); } //开始构建树 for (int i = 0; i < len/2; i++) { list.get(i).left = list.get(2*i+1).value!=flag?list.get(2*i+1):null; //记得处理最后一个父节点(len/2-1),因为有可能没有右孩子。 if(i<len/2-1 ||(i==len/2-1&& len%2!=0)){ list.get(i).right = list.get(2*i+2).value!=flag?list.get(2*i+2):null; } } return list.get(0); } public static void main(String[] args) { /***********************层次创建二叉树***********************/ String level_str = "1,2,3,4,5,6,7,8,9,-1,-1,-1,10,-1,-1";//层次 String[] array1 = level_str.split(","); int len = array1.length; int[] intlevelarray = new int[len]; for (int i = 0; i < len; i++) { intlevelarray[i] = Integer.valueOf(array1[i]); } TreeNode root5 = level_buildBTree(intlevelarray,-1); root1 = root5; }
1.4 前序和中序创建二叉树
/***从中序与先序遍历序列构造二叉树**/ public static TreeNode inpre_buildTree(int[] preOrder, int[] inorder) { TreeNode root = inpre_buildTreehelper(preOrder, 0, preOrder.length - 1, inorder, 0, inorder.length - 1); return root; } private static TreeNode inpre_buildTreehelper(int[] preOrder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd) { if (preStart > preEnd || inStart > inEnd) { return null; } int x = preOrder[preStart]; TreeNode root = new TreeNode(x); for (int i = inStart; i <= inEnd; i++) if (inorder[i] == x) { root.left = inpre_buildTreehelper(preOrder, preStart + 1, preStart + i - inStart, inorder, inStart, i - 1); root.right = inpre_buildTreehelper(preOrder, i - inStart + preStart + 1, preEnd, inorder, i + 1, inEnd); break; } return root; } public static void main(String[] args) { /***********************从中序与先序遍历序列构造二叉树***********************/ int[] in = {8,4,9,2,5,1,6,10,3,7}; int[] pre = {1,2,4,8,9,5,3,6,10,7}; root1 = inpre_buildTree(pre, in); }
1.5 后续和中序创建二叉树
/***从中序与后序遍历序列构造二叉树**/ public static TreeNode inpost_buildTree(int[] inorder, int[] postorder) { return inpost_buildTreehelper(postorder, 0, postorder.length - 1, inorder, 0, inorder.length - 1); } private static TreeNode inpost_buildTreehelper(int[] postorder,int postStart, int postEnd, int[] inorder, int inStart, int inEnd){ if (postStart > postEnd || inStart > inEnd) { return null; } int x = postorder[postEnd]; TreeNode root = new TreeNode(x); for (int i = inStart; i <= inEnd; i++) if (inorder[i] == x) { root.left = inpost_buildTreehelper(postorder, postStart, postEnd-(inEnd - i)-1, inorder, inStart, i - 1); root.right = inpost_buildTreehelper(postorder, postEnd-(inEnd - i), postEnd-1, inorder, i + 1, inEnd); break; } return root;
} public static void main(String[] args) { int[] in = {8,4,9,2,5,1,6,10,3,7}; int[] post = {8,9,4,5,2,10,6,7,3,1}; root1 = inpost_buildTree(in, post); }
1.6 括号表达式创建二叉树
//括号表达式构建二叉树 static TreeNode kuohao__buildTree(String input) { char[] str = input.toCharArray(); TreeNode root = null; TreeNode p = null; Stack<TreeNode> s = new Stack<TreeNode>(); int i = 0; int k = 0; char ch = str[i]; while(i<str.length){ switch(ch){ case '(':{ s.push(p);//括号左边的是父亲,入栈 k = 1;//括号右面的是左孩子 break; } case ',':{ k = 2;//逗号右边的是有孩子 break; } case ')':{ s.pop();//表示该节点的左右孩子已经确定,出栈 break; } default:{ int count = 0; boolean flag = false; while(i<str.length && (str[i] + "").matches("[0-9]")){ count = count * 10 + (str[i]-'0'); i++; flag = true; } if (flag = true) i--;//为了判断数字,多加了一次,所以减去 p = new TreeNode(count);//保存多位数字 if(root==null){ root = p;//保存根节点 }else{ if(k==1){ s.peek().left = p; }else if(k==2){ s.peek().right = p; } } break; } } i++; if(i<str.length){ ch = str[i]; } } return root; } public static void main(String[] args) { /***********************括号表达式构造二叉树***********************/ String input = "1(2(4(8,9),5),3(6(,10),7))"; TreeNode root6 = kuohao__buildTree(input); }
2. 二叉树的遍历
2.1 前序遍历(根左右)
/***递归先序遍历*/ public static void preOrder(TreeNode root,List<TreeNode> preorder){ if(root!=null){ preorder.add(root); preOrder(root.left,preorder); preOrder(root.right,preorder); } } /***非递归先序遍历*/ public static List<TreeNode> preOrderT(TreeNode root){ List<TreeNode> list = new LinkedList<TreeNode>(); Stack<TreeNode> stack = new Stack<TreeNode>(); if(root!=null){ stack.push(root); while(!stack.empty()){ TreeNode cur = stack.pop(); list.add(cur); if(cur.right!=null) stack.push(cur.right); if(cur.left!=null) stack.push(cur.left); } } return list; }
public static void main(String[] args) { System.out.println("==========递归先序遍历========="); List<TreeNode> preorder = new LinkedList<TreeNode>(); preOrder(root1,preorder);//递归先序遍历 printNonLevel(preorder);//打印 System.out.println("==========非递归先序遍历========="); List<TreeNode> preorderT = preOrderT(root1);//非递归先序遍历 printNonLevel(preorderT);//打印 } /***************************打印*************************/ /** * 打印一维链表(先序,中序,后序) * @param List<TreeNode> treeNode */ public static void printNonLevel(List<TreeNode> treeNode){ for (int i = 0; i < treeNode.size(); i++) { System.out.print(treeNode.get(i).value+" "); } System.out.println(); }
2.2 后序遍历(左右根)
addFirst
/***递归后序遍历*/ public static void postOrder(TreeNode root,List<TreeNode> postorder){ if(root!=null){ postOrder(root.left,postorder); postOrder(root.right,postorder); postorder.add(root); } } /***非递归后序遍历*/ public static List<TreeNode> postOrderT(TreeNode root){ LinkedList<TreeNode> list = new LinkedList<TreeNode>(); Stack<TreeNode> stack = new Stack<TreeNode>(); if(root!=null){ stack.push(root); while(!stack.empty()){ TreeNode cur = stack.pop(); list.addFirst(cur); if(cur.left!=null) stack.push(cur.left); if(cur.right!=null) stack.push(cur.right); } } return list; } public static void main(String[] args) { System.out.println("==========递归后序遍历========="); List<TreeNode> postorder = new LinkedList<TreeNode>(); postOrder(root1,postorder);//递归后序遍历 printNonLevel(postorder);//打印 System.out.println("==========非递归后序遍历========="); List<TreeNode> postorderT = postOrderT(root1);//递归后序遍历 printNonLevel(postorderT);//打印 } /***************************打印*************************/ /** * 打印一维链表(先序,中序,后序) * @param List<TreeNode> treeNode */ public static void printNonLevel(List<TreeNode> treeNode){ for (int i = 0; i < treeNode.size(); i++) { System.out.print(treeNode.get(i).value+" "); } System.out.println(); }
2.3 中序遍历(左根右)
/***递归中序遍历*/ public static void inOrder(TreeNode root, List<TreeNode> inorder){ if(root!=null){ inOrder(root.left,inorder); inorder.add(root); inOrder(root.right,inorder); } } /***非递归中序遍历*/ public static List<TreeNode> inOrderT(TreeNode root){ List<TreeNode> list = new LinkedList<TreeNode>(); Stack<TreeNode> stack = new Stack<TreeNode>(); TreeNode cur = root; while(cur!=null || !stack.empty()){ while(cur!=null){ stack.push(cur); cur = cur.left; } cur = stack.pop(); list.add(cur); cur = cur.right; } return list; } public static void main(String[] args) { System.out.println("==========递归中遍历========="); List<TreeNode> inorder = new LinkedList<TreeNode>(); inOrder(root1,inorder);//递归中序遍历 printNonLevel(inorder);//打印 System.out.println("==========非递归中序遍历========="); List<TreeNode> inorderT = inOrderT(root1);//非递归中序遍历 printNonLevel(inorderT);//打印 } /***************************打印*************************/ /** * 打印一维链表(先序,中序,后序) * @param List<TreeNode> treeNode */ public static void printNonLevel(List<TreeNode> treeNode){ for (int i = 0; i < treeNode.size(); i++) { System.out.print(treeNode.get(i).value+" "); } System.out.println(); }
2.4 广度优先遍历(层次遍历)
/***广度优先遍历或者层次遍历*/ public static List<List<TreeNode>> levelOrder(TreeNode root) { List<List<TreeNode>> res = new LinkedList<>(); if (root == null) { return res; } levelOrderHelper(res, root, 0); return res; } /**二叉树的深度*/ private static void levelOrderHelper(List<List<TreeNode>> res, TreeNode root, int depth) { if (root == null) { return; } if (res.size() <= depth) { res.add(new LinkedList<>());// 当前层的第一个节点,需要 new 一个 list 来存当前层. } res.get(depth).add(root);// depth 层,把当前节点加入 // 递归的遍历下一层. levelOrderHelper(res, root.left, depth + 1); levelOrderHelper(res, root.right, depth + 1); }
/**非递归 广度优先遍历或者层次遍历,用队列实现层次遍历*/ public static List<List<TreeNode>> levelOrderT(TreeNode root) { if(root == null) return new ArrayList<>(); List<List<TreeNode>> list = new ArrayList<>();
if(root == null) return list; Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.offer(root); while(!queue.isEmpty()){ int count = queue.size(); List<TreeNode> levellist = new ArrayList<TreeNode>(); while(count > 0){ TreeNode node = queue.poll(); levellist.add(node); if(node.left != null) queue.offer(node.left); if(node.right != null) queue.offer(node.right); count--; } list.add(levellist); } return list; }
public static void main(String[] args) { System.out.println("==========递归广度优先遍历 OR 层次遍历========="); List<List<TreeNode>> levelOrder = levelOrder(root1); printLevel(levelOrder); System.out.println("==========非递归层次遍历========="); List<List<TreeNode>> levelOrderT = levelOrderT(root1); printLevel(levelOrderT); }
/** * 打印二维链表(层次) * @param List<List<TreeNode>> treeNode */ public static void printLevel(List<List<TreeNode>> levelOrder){ for (int i = 0; i < levelOrder.size(); i++) { for (int j = 0; j < levelOrder.get(i).size(); j++) { System.out.print(levelOrder.get(i).get(j).value +" "); } System.out.println(); } }
2.4 深度优先遍历
/*** 深度优先遍历*/ public static void dfs(TreeNode node, List<List<TreeNode>> dfsResult, List<TreeNode> list) { if (node == null) return; if (node.left == null && node.right == null) { list.add(node); dfsResult.add(new ArrayList<>(list));//不能直接将list存入,需要新建一个list来实现,防止后序操作影响 list.remove(list.size() - 1);//将其最后一个存的节点删掉回溯 } list.add(node); dfs(node.left, dfsResult, list); dfs(node.right, dfsResult, list); list.remove(list.size() - 1); } public static void main(String[] args) { System.out.println("==========非递归层次遍历========="); List<List<TreeNode>> levelOrderT = levelOrderT(root1); printLevel(levelOrderT); } /** * 打印二维链表(层次) * @param List<List<TreeNode>> treeNode */ public static void printLevel(List<List<TreeNode>> levelOrder){ for (int i = 0; i < levelOrder.size(); i++) { for (int j = 0; j < levelOrder.get(i).size(); j++) { System.out.print(levelOrder.get(i).get(j).value +" "); } System.out.println(); } }

