数据结构与算法系列——排序(6)_树形选择排序
1. 工作原理（定义）
树形选择排序（Tree Selection Sort），又称锦标赛排序（Tournament Sort），是一种按照锦标赛思想进行选择排序的方法。
首先对n个记录的关键字进行两两比较，然后在其中[n/2]（向上取整）个较小者之间再进行两两比较，如此重复，直至选出最小关键字的记录为止。
胜者树和败者树是完全二叉树，是树形选择排序的变形。
2. 算法步骤
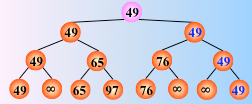
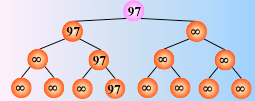
这个过程可以用一棵有n个叶子结点的完全二叉树表示。如图中的二叉树表示从8个关键字中选出最小关键字的过程：
8个叶子结点中依次存放排序之前的8个关键字，每个非终端结点中的关键字均等于其左、右孩子结点中较小的那个关键字，则根结点中的关键字为叶子结点中的最小关键字。
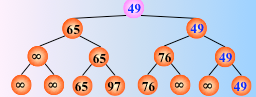
在输出最小关键字之后，根据关系的可传递性，欲选出次小关键字，仅需将叶子结点中的最小关键字（13）改为“最大值”，然后从该叶子结点开始，和其左右兄弟的关键字进行比较，修改从叶子结点到根结点的路径上各结点的关键字，则根结点的关键字即为次小值。
同理，可依次选出从小到大的所有关键字。
3. 图示
为了减少简单选择排序，我们利用前n-1次比较信息，减少下次选择。类似于锦标赛。根据锦标赛传递关系。亚军只能从被冠军击败的人中选出。 
实际算法中，我们把需要比较的记录全部作为叶子，然后从叶子开始两两比较，从底向上最后形成一棵完全二叉树。在我们选择出最小关键字后，根据关系的传递，只需要将最小关键字的叶子节点改成无穷大，重新从底到上比较一次就能够得出次小关键字。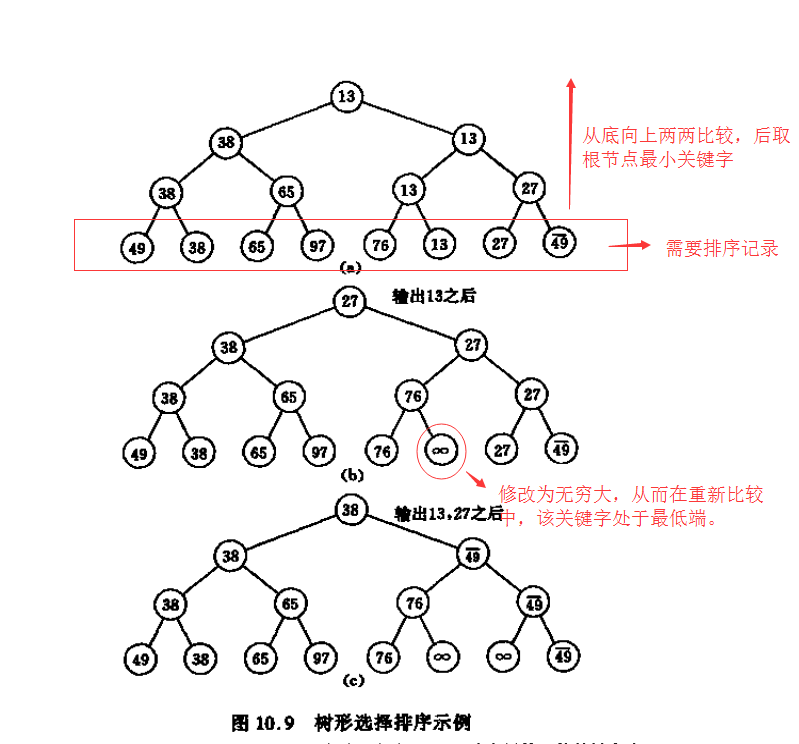 
然而虽然树形选择比较能够减少比较次数，却增加了辅助空间的使用。为了弥补此缺憾，威廉姆斯于1964年提出了堆排序。
具体的例子：
对 n 个关键字两两比较，直到选出最小关键字为止，一趟排序结束
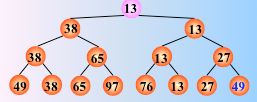
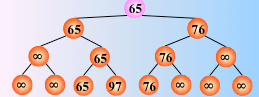
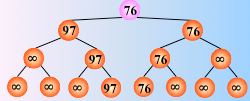
反复这个过程，仅需将叶子结点的最小关键字改为最大值∞，即可
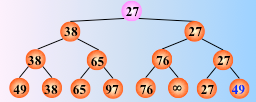
然后从该叶子结点开始，继续和其左右兄弟的关键字比较，找出最值
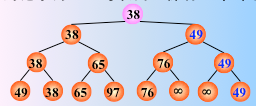
4. 性能分析
1. 时间复杂度
时间复杂度：由于含有 n 个叶子结点的完全二叉树的深度为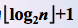
，则在树形选择排序中，除了最小关键字外，每选择一个次小关键字仅需进行 
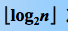次比较，故时间复杂度为 O(n logn)。
缺点： 1、与“∞”的比较多余； 2、辅助空间使用多。
为了弥补这些缺点，1964年，堆排序诞生。
2. 空间复杂度
选择排序过程中，需要临时变量存储待排序元素，因此空间复杂度为O(n)。
3. 算法稳定性
选择排序是不稳定的算法，在选择数值和交换过程中它们的顺序可能会发生变化。
6. 具体代码
import java.util.Arrays; public class TreeSelectionSort{ public static void main(String[] args) { int[] arr = {8,7,6,5,4,3,2,1}; System.out.println(Arrays.toString(treeSelectionSort(arr))); } public static int[] treeSelectionSort(int[] mData) { int n = mData.length; int MinValue = Integer.MIN_VALUE; // 得到树上节点的个数 int baseSize = 1; while (baseSize < n) { baseSize *= 2; } int treeSize = baseSize * 2 - 1;// 树的大小 // 初始化树,从下标1-treeSize,忽略下标0 int[] tree = new int[treeSize+1]; int i = 0; for (; i < n; i++) { tree[treeSize - i] = mData[i]; } for (; i < baseSize; i++) { tree[treeSize - i] = MinValue; } // 构造一棵树 for (i = treeSize; i > 1; i -= 2) { tree[i / 2] = (tree[i] > tree[i - 1] ? tree[i] : tree[i - 1]); } //每一趟得到一个最大值 while (n > 0 ) { // 根节点是最大值 int max = tree[1]; // 倒着放入数组之后得到的正向数组就是 从小到大 mData[--n] = max; // 将叶子节点中最大值的位置赋值为最小值 int maxIndex = treeSize; while (tree[maxIndex] != max) { maxIndex--; } tree[maxIndex] = MinValue; // 重新调整胜者树的值 while (maxIndex > 1) { if (maxIndex % 2 == 0) { tree[maxIndex / 2] = (tree[maxIndex] > tree[maxIndex + 1] ? tree[maxIndex] : tree[maxIndex + 1]); } else { tree[maxIndex / 2] = (tree[maxIndex] > tree[maxIndex - 1] ? tree[maxIndex] : tree[maxIndex - 1]); } maxIndex /= 2; } } return mData; } }
