数据结构与算法系列——排序(8.2)_鸡尾酒排序

1. 工作原理（定义）

　　核心思想：鸡尾酒排序是冒泡排序的一种改进和变型 ，又称“双向冒泡排序”，鸡尾酒排序是从低到高然后从高到低来回排序（选出最大和最小项），比冒泡排序的效率稍微好一点，原因是冒泡排序只从一个方向进行比对(由低到高)，每次循环只移动一个项目。 

2. 算法步骤

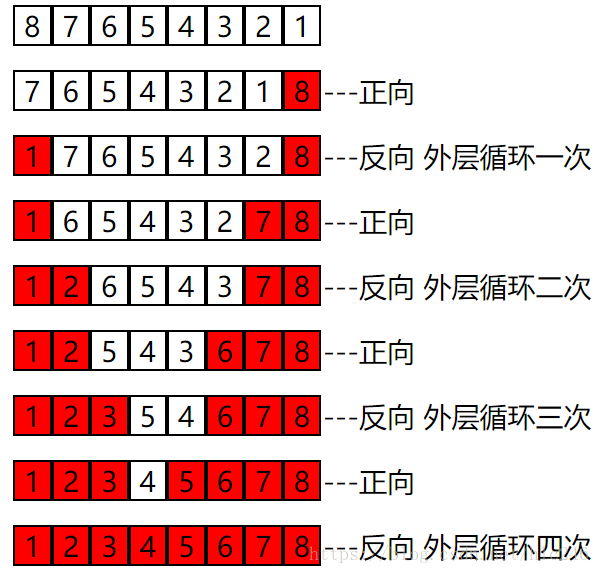
1. 先对数组从左到右进行冒泡排序（升序），则最大的元素去到最右端 
2. 再对数组从右到左进行冒泡排序（降序），则最小的元素去到最左端 
3. 循环1、2步操作，依次改变冒泡的方向，并不断缩小未排序元素的范围，直到最后一个元素结束

　　

4. 性能分析

　　鸡尾酒排序是冒泡排序的一种改进，倒并未有本质的改变，与冒泡排序的时间复杂度和空间复杂度相近，整体的性能都比较差。

1. 时间复杂度

　　（1）顺序排列时，鸡尾酒排序时间复杂度为O(n)； 
　　（2）逆序排序时，鸡尾酒排序时间复杂度为O(n^2)； 
　　（3）当原始序列杂乱无序时，平均时间复杂度为O(n^2)。

2. 空间复杂度

　　鸡尾酒排序排序过程中，Swap函数需要一个临时变量temp进行两两交换，所需要的额外空间为1，因此空间复杂度为O(1)。

3. 算法稳定性 

　　鸡尾酒排序是一种稳定的排序算法。

5. 具体代码

public class CockTailSort{
    public static void main(String[] args) {
        int[] arr = {8,7,6,5,4,3,2,1};
        cockTailSort(arr);
    }

    public static void cockTailSort(int[] arr) {
        boolean isSorted=false;
        int length = arr.length;
        //双向同时进行
        for(int i=0;i<length/2;i++) {
            isSorted=false;
            //升序排列
            for(int j=i;j<length-i-1;j++) {
                if(arr[j]>arr[j+1]) {
                    swap(arr, j, j + 1);
                    isSorted=true;
                }
            }
            //降序排列
            for(int j=length-i-1;j>i;j--) {
                if(arr[j] < arr[j-1]) {
                     swap(arr, j, j - 1);
                    isSorted=true;
                }
            }

            if(isSorted==false) {
                break;
            }
        }
    }
    //交换
    private static void swap(int[] arr, int a, int b) {
        int tmp = arr[a];
        arr[a] = arr[b];
        arr[b] = tmp;
    }
}

6. 参考网址

1. 排序算法系列之鸡尾酒排序