数据结构与算法系列——排序(14)_桶排序
1. 工作原理(定义)
桶排序的思想近乎彻底的分治思想。桶排序是鸽巢排序的一种归纳结果。
桶排序 (Bucket sort)或所谓的箱排序,是一个非比较排序算法,是基于映射函数实现的。工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间(Θ(n))。
桶排序是计数排序的升级版【可以实数】。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
- 在额外空间充足的情况下,尽量增大桶的数量
- 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中【在桶排序中保证元素均匀分布到各个桶尤为关键。】
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
2. 算法步骤
- 根据输入建立适当个数的桶,每个桶可以存放某个范围内的元素;【根据待排序集合中最大元素和最小元素的差值范围和映射规则(映射函数一般是 f = array[i] / k,k^2 = n; n是所有元素个数),确定申请的桶个数;】
- 将落在特定范围内的所有元素放入对应的桶中;
- 对每个非空的桶中元素进行排序,可以选择通用的排序方法,比如插入、快排;
- 按照划分的范围顺序,将桶中的元素依次取出。排序完成。

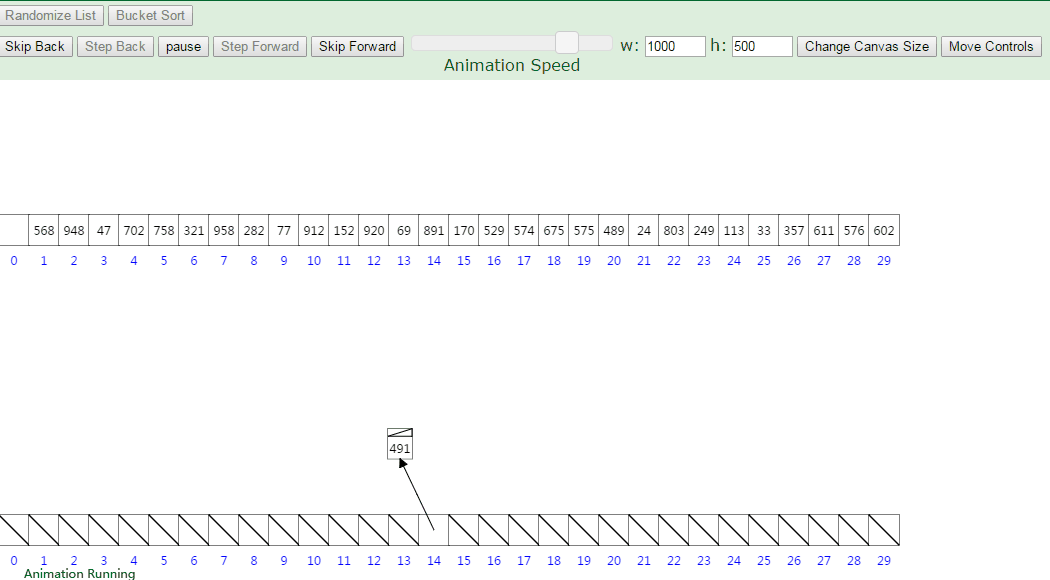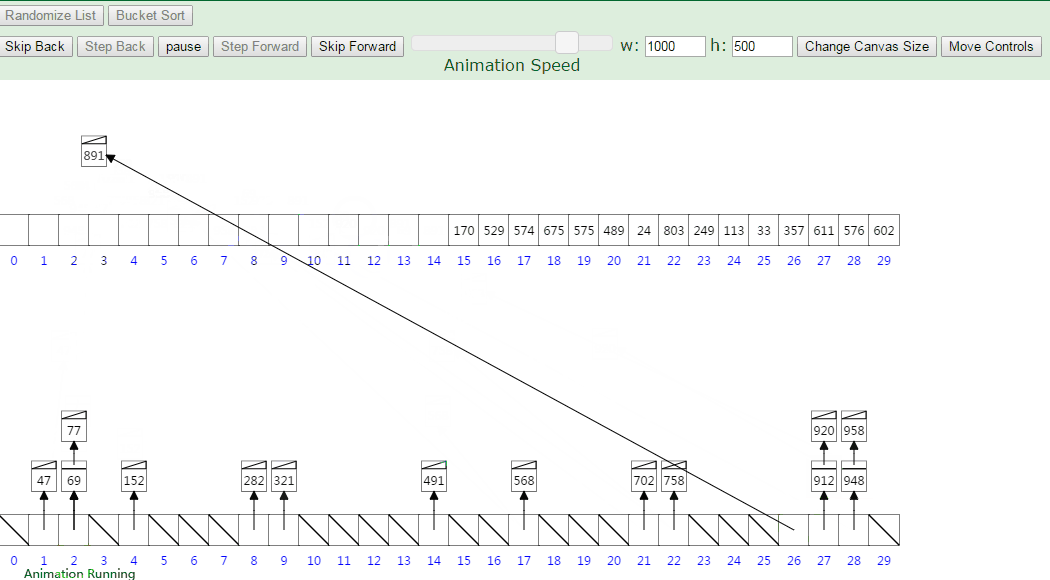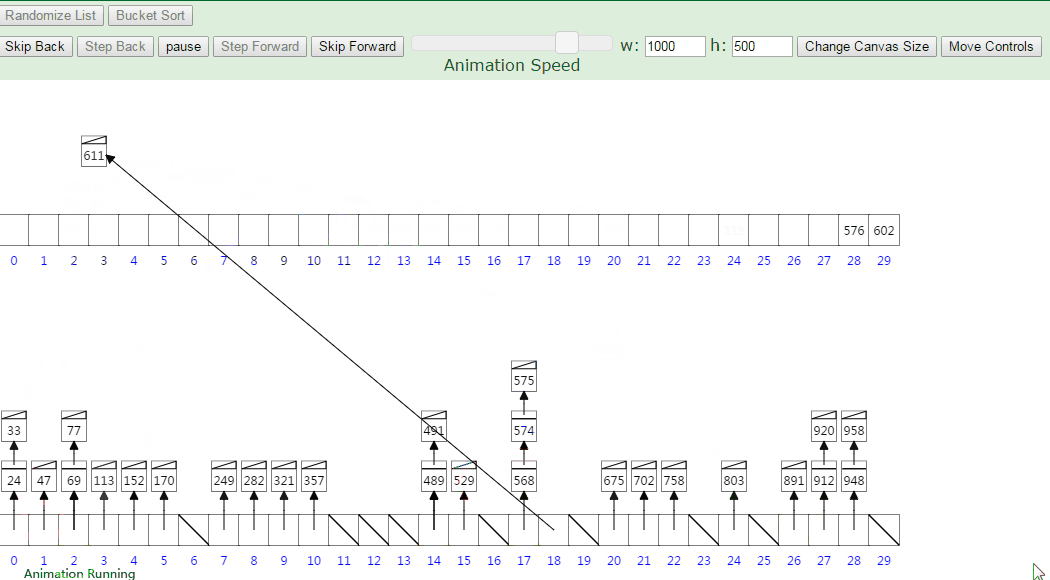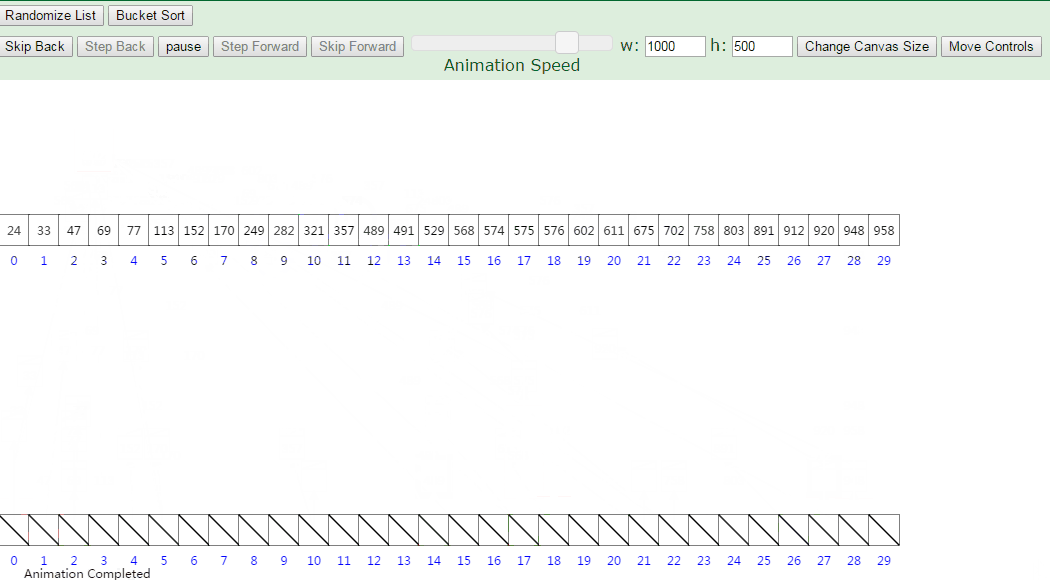
元素分布在桶中:
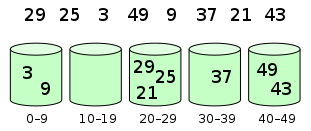
然后,元素在每个桶中排序:

3. 动画演示
Linked List Array index = Value * NUMBER_OF_ELEMENTS / (MAXIMUM_ARRAY_VALUE +1) = (value * 30)/1000
MAXIMUM_ARRAY_VALUE 加1是为了保证最大元素可以存到数组最后一个位置,即arr.length - 1处。
4. 性能分析
1. 时间复杂度
对于N个待排数据,M个桶,平均每个桶[N/M]个数据的桶排序平均时间复杂度为:O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM),桶排序的平均时间复杂度为线性的O(N+C),其中C=N*(logN-logM)。
当M=N时,即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。
当M=1时,即极限情况下只有一个桶时。桶排序的最坏效率达到O(N*logN)。
- 最坏时间复杂度:O(N*logN)。
- 最好时间复杂度:O(N)。
- 平均时间复杂度:O(N+N*logN-N*logM)
2. 空间复杂度
桶排序的空间复杂度 为O(N+M),如果输入数据非常庞大,而桶的数量也非常多,则空间代价较大。
3. 算法稳定性
桶排序是稳定的算法。【桶排序可以是稳定的。这取决于我们对每个桶中的元素采取何种排序方法,比如桶内元素的排序使用快速排序,那么桶排序就是不稳定的;如果使用的是插入排序,桶排序就是稳定的。】
6. 优缺点
桶排序也不能很好地应对元素值跨度很大的数组。比如[3, 2, 1, 0 ,4, 8, 6, 999],按照上面的映射规则,999会放入一个桶中,剩下所有元素都放入同一个桶中,在各个桶中元素分布极不均匀,这就失去了桶排序的意义。
桶排序和计数排序有个共同的缺点:耗费大量空间。
再细看桶排序,其实计数排序可以看作是桶排序的一种特例,计数排序相当于将所有相同的元素放入同一个桶中,而桶排序可以将一定范围内的元素都放入同一个桶中;另外,桶排序的数据结构很像基于拉链法的散列表,只是定义的映射函数不同。桶排序的映射函数将较大值映射成较大的索引,这两者是呈正相关的。而散列表的映射函数得到的哈希值是随意的。
7. 应用
7. 具体代码
import java.util.ArrayList; import java.util.Arrays; import java.util.*; public class BucketSort{
// 一般创建的桶数量等于原始数列的元素数量,除了最后一个桶只包含数列最大值,前面各个桶的区间按照比例确定。【OR 桶数量等于原始数列的元素数量+1,除了第一个桶只包含数列最小值,最后一个桶只包含数列最大值,中间各个桶的区间按照比例确定。】
// 区间跨度 = (最大值-最小值)/ (桶的数量 - 1)
// 定位元素属于第几个桶,是按照比例来定位:(array[i] - min) * (bucketNum-1) / (max - min)
public static double[] bucketSort(double[] array, int bucketNum){ //1.得到数列的最大值和最小值,并算出差值d double max = array[0]; double min = array[0]; for(int i=1; i<array.length; i++) { if(array[i] > max) { max = array[i]; } if(array[i] < min) { min = array[i]; } } // 下面的运行慢 // double max = Arrays.stream(array).max().getAsDouble(); // double min = Arrays.stream(array).min().getAsDouble(); double d = max - min; //2.初始化桶 //int bucketNum = array.length; ArrayList<LinkedList<Double>> bucketList = new ArrayList<LinkedList<Double>>(bucketNum); for(int i = 0; i < bucketNum; i++){ bucketList.add(new LinkedList<Double>()); } //3.遍历原始数组,将每个元素放入桶中 for(int i = 0; i < array.length; i++){ int num = (int)((array[i] - min) * (bucketNum-1) / d); bucketList.get(num).add(array[i]); } //4.对每个通内部进行排序 for(int i = 0; i < bucketList.size(); i++){ //JDK底层采用了归并排序或归并的优化版本 Collections.sort(bucketList.get(i)); } //5.输出全部元素 double[] sortedArray = new double[array.length]; int index = 0; for(LinkedList<Double> list : bucketList){ for(double element : list){ sortedArray[index] = element; index++; } } return sortedArray; } public static void main(String[] args) { double[] array = new double[] {4.12,6.421,0.0023,3.0,2.123,8.122,4.12, 10.09}; double[] sortedArray = bucketSort(array,3); System.out.println(Arrays.toString(sortedArray)); } }