数据结构与算法系列——排序(12)_计数排序
1. 工作原理(定义)
计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序,堆排序)
计数排序是一种稳定的线性时间排序算法。计数排序使用一个额外的数组 C ,其中第i个元素是待排序数组 A中值等于 i的元素的个数。然后根据数组 C 来将 A中的元素排到正确的位置。
2. 算法步骤
(1)找出待排序的数组中最大和最小的元素,确定数组大小C[max-min+1]。
(2)统计数组中每个值为i的元素出现的次数,存入数组C的第i项
(3)对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
(4)反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
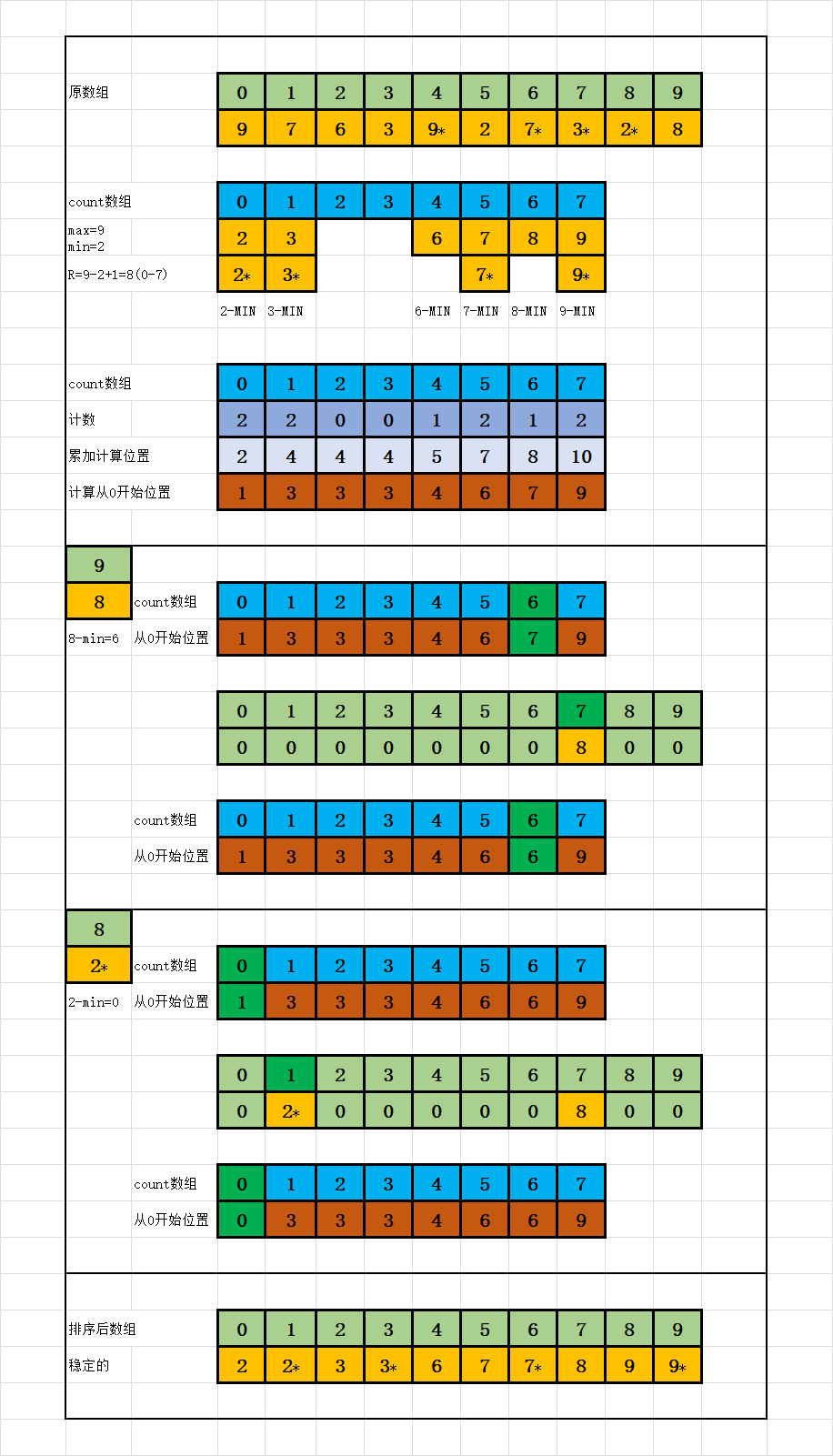
3. 动画演示

4. 性能分析
1. 时间复杂度
当输入的元素是 n 个 0 到 k 之间的整数时,它的运行时间是 Θ(n + k)。计数排序不是比较排序,排序的速度快于任何比较排序算法。故时间复杂度为O(N)。
2. 空间复杂度
排序过程中,需要一个辅助空间,因此空间复杂度为O(n)。
3. 算法稳定性
是稳定的算法。
4. 初始顺序状态
- 比较次数:
- 移动次数:
- 复杂度:
- 排序趟数:
5. 归位
6. 优点
它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序,堆排序)
7. 具体代码
import java.util.Arrays; public class CountingSort { public static void main(String[] args) { int[] a = {9, 7, 6, 3, 9, 2, 7, 3, 2, 8}; countingSort(a); System.out.println(Arrays.toString(a)); } //方法1,归位的时候是反向 public static void countingSort(int[] arr) { // 计算最大最小值,严谨实现最好用ifPresent检查下 int max = Arrays.stream(arr).max().getAsInt(); int min = Arrays.stream(arr).min().getAsInt(); int N = arr.length; int R = max - min + 1; // 最大最小元素之间范围[min, max]的长度 // 1. 计算频率,在需要的数组长度上额外加1 int[] count = new int[R]; for (int i = 0; i < N; i++) { // 使用加1后的索引,有重复的该位置就自增 count[arr[i] - min]++; } // 2. 频率 -> 元素的开始索引 for (int r = 1; r < R; r++) { count[r] += count[r-1]; } // 3. 元素按照开始索引分类,用到一个和待排数组一样大临时数组存放数据 int[] aux = new int[N]; for (int i = N-1; i >=0; i--) { // 填充一个数据后,自增,以便相同的数据可以填到下一个空位 aux[count[arr[i] - min]-1] = arr[i]; count[arr[i] - min]--; } // 4. 数据回写 for (int i = 0; i < N; i++) { arr[i] = aux[i]; } } //方法2,归位的时候是正向 public static void countingSort2(int[] arr) { // 计算最大最小值,严谨实现最好用ifPresent检查下 int max = Arrays.stream(arr).max().getAsInt(); int min = Arrays.stream(arr).min().getAsInt(); int N = arr.length; int R = max - min + 1; // 最大最小元素之间范围[min, max]的长度 // 1. 计算频率,在需要的数组长度上额外加1 int[] count = new int[R+1]; for (int i = 0; i < N; i++) { // 使用加1后的索引,有重复的该位置就自增 count[arr[i] - min + 1]++; } // 2. 频率 -> 元素的开始索引 for (int r = 0; r < R; r++) { count[r + 1] += count[r]; } // 3. 元素按照开始索引分类,用到一个和待排数组一样大临时数组存放数据 int[] aux = new int[N]; for (int i = 0; i < N; i++) { // 填充一个数据后,自增,以便相同的数据可以填到下一个空位 aux[count[arr[i] - min]++] = arr[i]; } // 4. 数据回写 for (int i = 0; i < N; i++) { arr[i] = aux[i]; } } }
反向图解释