数据结构与算法系列——排序(11)_基数排列
1. 工作原理(定义)
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
2. 算法步骤
最高位优先(Most Significant Digit first)法,简称MSD法:先按k1排序分组,同一组中记录,关键码k1相等,再对各组按k2排序分成子组,之后,对后面的关键码继续这样的排序分组,直到按最次位关键码kd对各子组排序后。再将各组连接起来,便得到一个有序序列。
最低位优先(Least Significant Digit first)法,简称LSD法:先从kd开始排序,再对kd-1进行排序,依次重复,直到对k1排序后便得到一个有序序列。
LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好。
-
将所有待比较数值(正整数)统一为同样的数位长度(最大元素长度),数位较短的数前面补零。
-
从最低位开始,依次进行一次排序。
-
重复操作,直至完成最高位的排序。
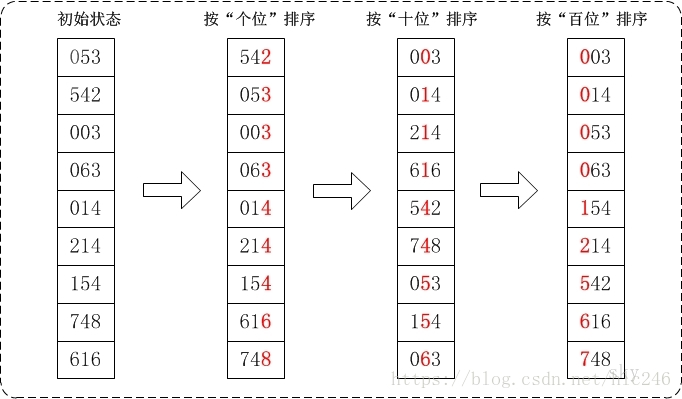
3. 动画演示

4. 性能分析
1. 时间复杂度
时间复杂度为:k* length;其中 k为数组元素最高位数,length为元素个数;故时间复杂度为O(K*N)。
在基数排序中,因为没有比较操作,所以在复杂上,最好的情况与最坏的情况在时间上是一致的。因此无论是最好,最坏还是平均复杂度都是O(d * (n + r))。其中,d 为位数,r 为基数,n 为原数组个数。
设待排序列为n个记录,d个关键码,关键码的取值范围为radix,则进行链式基数排序的时间复杂度为O(d(n+radix)),其中,一趟分配时间复杂度为O(n),一趟收集时间复杂度为O(radix),共进行d趟分配和收集。 空间效率:需要2*radix个指向队列的辅助空间,以及用于静态链表的n个指针。
2. 空间复杂度
空间复杂度O(n+dr)
3. 算法稳定性
稳定的算法。
4. 初始顺序状态
- 比较次数:
- 移动次数:
- 复杂度:
- 排序趟数:
5. 归位
不能归位
6. 优点
7. 具体代码
普通正整数
import java.util.ArrayList; import java.util.List; public class RadixSort { /** * MSD方法1--两个数组,基于计数排序 * @param arr */ public static void radixSortMSD(int[] arr) { int exp; // 指数。当对数组按各位进行排序时,exp=1;按十位进行排序时,exp=10;... int max = getMax(arr); //最大值 int maxDigit = maxDigit(max);//最大数位 for (exp = (int) Math.pow(10, maxDigit-1); exp >1 ; exp /= 10){//高位->低位 countingSort(arr, exp); } } /** * LSD 方法1--两个数组,基于计数排序 * @param arr */ public static void radixSort(int[] arr) { int exp; // 指数。当对数组按各位进行排序时,exp=1;按十位进行排序时,exp=10;... int max = getMax(arr);// 数组arr中的最大值 for (exp = 1; max/exp > 0; exp *= 10){//低位->高位 countingSort(arr, exp); } } public static void countingSort(int[]arr, int exp){ int[] output = new int[arr.length]; // 存储"被排序数据"的临时数组 int[] buckets = new int[10]; // 将数据出现的次数存储在buckets[]中 for (int i = 0; i < arr.length; i++){ buckets[ (arr[i]/exp)%10 ]++; } // 更改buckets[i]。目的是让更改后的buckets[i]的值,是该数据在output[]中的位置。 for (int i = 1; i < 10; i++) buckets[i] += buckets[i - 1]; // 将数据存储到临时数组output[]中 for (int i = arr.length - 1; i >= 0; i--) { output[buckets[ (arr[i]/exp)%10 ] - 1] = arr[i]; buckets[ (arr[i]/exp)%10 ]--; } // 将排序好的数据赋值给a[] for (int i = 0; i < arr.length; i++){ arr[i] = output[i]; } } /** * LSD 方法2--二维数组 * @param arr */ public static void radixSort2(int[] arr) { int maxDigit = maxDigit(getMax(arr)); int digitValue=1;//代表位数对应的数:1,10,100... int RADIX = 10; int length=arr.length; int[][] bucket=new int[RADIX][length];//排序桶用于保存每次排序后的结果,这一位上排序结果相同的数字放在同一个桶里 int[] order=new int[RADIX];//用于保存每个桶里有多少个数字 while(digitValue < Math.pow(RADIX, maxDigit+1)) { for(int num:arr) { //将数组arr里的每个数字放在相应的桶里 int digit=(num/digitValue)%RADIX; bucket[digit][order[digit]]=num; order[digit]++; } int k=0;//保存每一位排序后的结果用于下一位的排序输入 for(int i=0;i<RADIX;i++) {//将前一个循环生成的桶里的数据覆盖到原数组中用于保存这一位的排序结果 if(order[i]!=0) {//这个桶里有数据,从上到下遍历这个桶并将数据保存到原数组中 for(int j=0;j<order[i];j++) { arr[k++]=bucket[i][j]; } } order[i]=0;//将桶里计数器置0,用于下一次位排序 } digitValue*=RADIX; } } /** * LSD 方法3--数组列表 * @param arr */ public static void radixSort3(int[] arr) { int maxDigit = maxDigit(getMax(arr)); List<List<Integer>> list = new ArrayList<List<Integer>>(); for(int i = 0; i < 10; i ++) { list.add(new ArrayList<Integer>()); } for(int i = 0, factor = 1; i < maxDigit; factor *= 10, i ++) { for(int j = 0; j < arr.length; j ++) { list.get((arr[j]/factor)%10).add(arr[j]); } for(int j = 0, k = 0; j < list.size(); j ++) { while(!list.get(j).isEmpty()) { arr[k] = list.get(j).get(0); list.get(j).remove(0); k ++; } } } } /** * LSD 方法4--队列 * @param arr */ public static void radixSort4(int[] arr) { //求最大位数 int count = maxDigit(getMax(arr)); int len = arr.length; //十个队列,分别存储数位数值为0-9的元素 BucketQueue [] queues = new BucketQueue[10]; //各队列初始化 for(int i = 0; i < 10; i++) { queues[i] = new BucketQueue(); queues[i].data = new int[len]; queues[i].front = queues[i].rear = -1; } int m = 1;//m控制取第几位(从个位开始取直到count) while(count > 0) { for(int i = 0; i < len; i++) { int t = arr[i] / m % 10; //根据数值分配入队 queues[t].data[++queues[t].rear] = arr[i]; } //从队号0-9顺序出队收集元素 int s = 0; for(int j = 0; j < 10; j++) { while(queues[j].front != queues[j].rear) { arr[s++] = queues[j].data[++queues[j].front]; } //收集后队列清空,方便下一趟排序 queues[j].front = queues[j].rear = -1; } m *= 10; count--; } } /** * 获取数组arr中最大值 */ private static int getMax(int[] arr) { int max; max = arr[0]; for (int i = 1; i < arr.length; i++){ if (arr[i] > max){ max = arr[i]; } } return max; } //计算数组里元素的最大位数 private static int maxDigit(int max) { if (max == 0) { return 1; } int lenght = 0; for (int temp = max; temp != 0; temp /= 10) { lenght++; } return lenght; } public static void main(String[] args) { int[] A=new int[]{73,22, 93, 43, 55, 14, 28, 65, 39, 81}; radixSortMSD(A); for(int num:A) { System.out.println(num); } } } class BucketQueue { int data[]; int front; int rear; }
字符串
public class RadixSort { public static void main(String[] args) { String[] words = {"Java", "Mongodb", "Redis", "Kafka", "javascript", "mysql", "mybatis", "kindle", "rpc", "Algorithm", "mergeSort", "quickSort", "Adobe"}; radixSort(words); for (String word : words) { System.out.println(word.replaceAll("0", "")); } } //基数排序(单词 private static void radixSort(String[] words){ int exp = 0; int maxLength = getMaxLength(words); autoComplete(words, maxLength); for(exp = 1; exp <= maxLength; exp++){ countingSort(words, exp); } } //计数排序(单词) private static void countingSort(String[] words, int exp){ int n = words.length; String[] r = new String[n]; int[] c = new int[122]; for(int i = 0; i < n; ++i){ int asc = (byte)words[i].charAt(words[i].length() - exp); c[asc]++; } for(int i = 1; i < 122; ++i){ c[i] = c[i-1] + c[i]; } for (int i = n - 1; i >= 0; --i){ int asc = (byte)words[i].charAt(words[i].length() - exp); int index = c[asc]; r[index - 1] = words[i]; c[asc]--; } for(int i = 0; i < n; ++i){ words[i] = r[i]; } } //自动补全单词 private static void autoComplete(String[] words, int maxLength){ int i = 0; for (String word : words) { if(word.length() < maxLength){ int value = maxLength - word.length(); StringBuilder sb = new StringBuilder(); for(int j = 0; j < value; ++j){ sb.append("0"); } words[i] = word + sb; } i++; } } //获取字符串最大的长度 private static int getMaxLength(String[] words){ int maxLength = words[0].length(); for(int i = 1; i < words.length; ++i){ if(words[i].length() > maxLength) maxLength = words[i].length(); } return maxLength; } }

