数据结构与算法系列——排序(10)_归并排序
1. 工作原理(定义)
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法,指的是将两个已经排序的序列合并成一个序列的操作。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
- 自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第 2 种方法);
- 自下而上的迭代;
2. 算法步骤
1. 从下往上的归并排序【迭代】:
-
通过分治法将长度为n的序列划分为n个长度为1的子序列。
-
进行两两归并比较,得到 n/2 个长度为 2 的有序子序列
-
重复第 2 步,直到所有子序列归并成一个长度为 n 的有序序列。
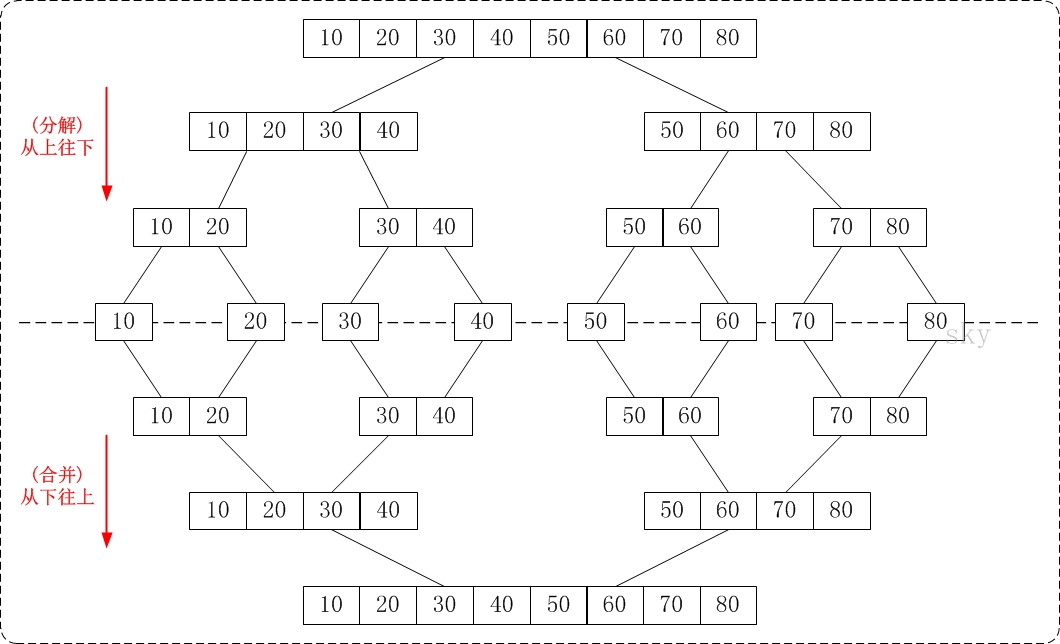
2. 从上往下的归并排序【递归】:
-
分解 -- 将当前区间一分为二,即求分裂点 mid = (low + high)/2;
-
求解 -- 递归地对两个子区间a[low...mid] 和 a[mid+1...high]进行归并排序。递归的终结条件是子区间长度为1。
-
合并 -- 将已排序的两个子区间a[low...mid]和 a[mid+1...high]归并为一个有序的区间a[low...high]。
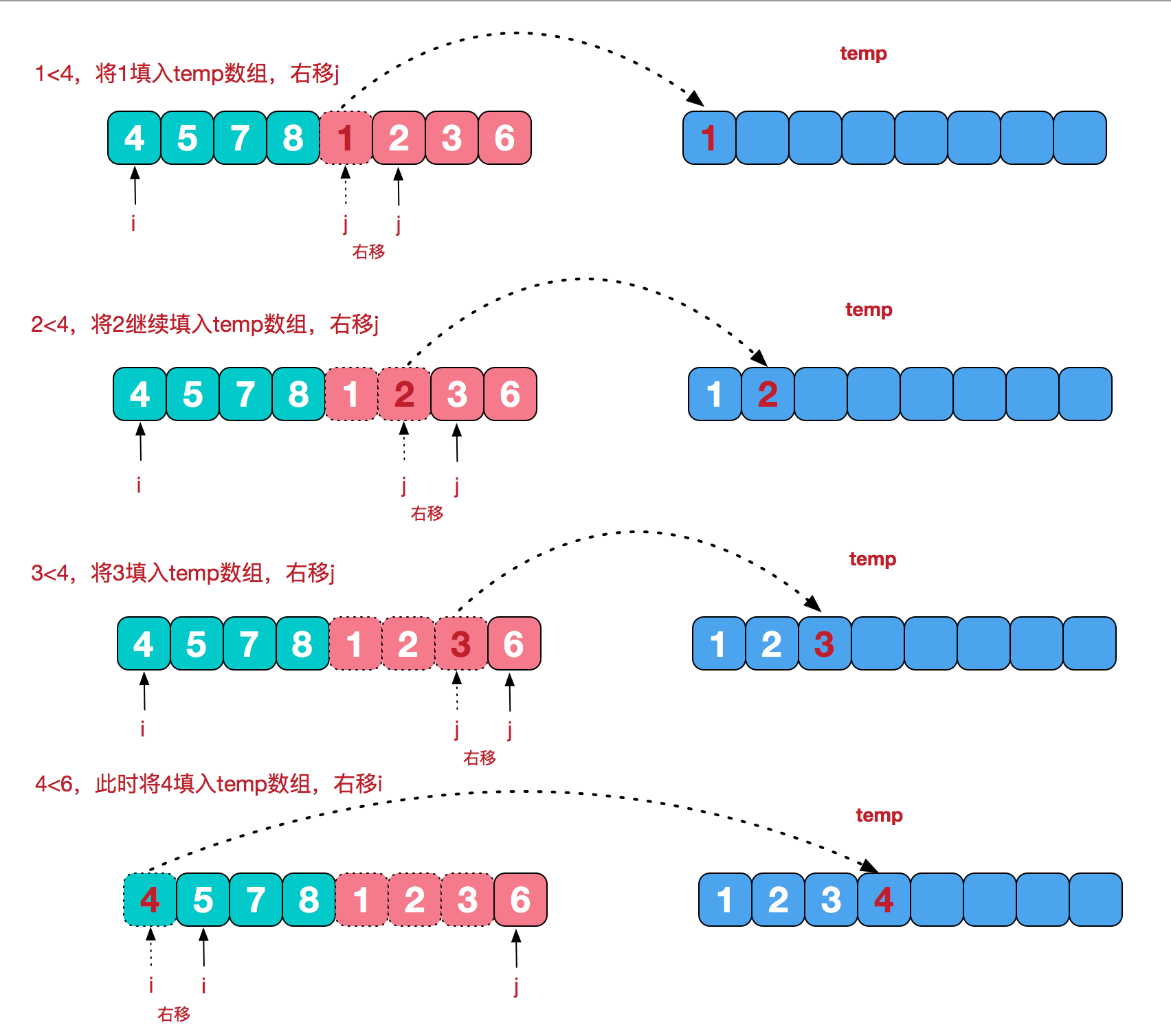
3. 归并步骤:
-
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
-
设定两个指针,最初位置分别为两个已经排序序列的起始位置;
-
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
-
重复步骤 3 直到某一指针达到序列尾;
-
将另一序列剩下的所有元素直接复制到合并序列尾。
3. 动画演示


4. 性能分析
1. 时间复杂度
归并排序的效率是比较高的,设数列长为N,将数列分开成小数列一共要 logN 步,每步都是一个合并有序数列的过程,时间复杂度可以记为O(N),故一共为O(N*logN),故时间复杂度为O(nlogn)。
2. 空间复杂度
归并排序过程中,需要一个辅助空间来暂存两有序子文件归并的结果,因此空间复杂度为O(n)。
3. 算法稳定性
归并是稳定的算法,在分解和并归过程中元素相对顺序未发生改变。
4. 初始顺序状态
- 比较次数:
- 移动次数:
- 复杂度:
- 排序趟数:
5. 归位
不能归位
6. 优点
- 排序:速度仅次于快速排序,为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列
- 求逆序对数:在归并的过程中计算每个小区间的逆序对数,进而计算出大区间的逆序对数(也可以用树状数组来求解)
7. 具体代码
public class MergeSort { // 归并排序(从上往下,递归) public static void mergeSortUp2Down(int [] arr, int start, int end){ if(arr!=null && start<end){//当子序列中只有一个元素时结束递归 int mid=(start+end)/2;//划分子序列 mergeSortUp2Down(arr, start, mid);//对左侧子序列进行递归排序 mergeSortUp2Down(arr, mid+1, end);//对右侧子序列进行递归排序 merge(arr, start, mid, end);//合并 } } //归并排序(从下往上,迭代) public static void mergeSortDown2Up(int [] arr){ if(arr!=null){ int len = arr.length; //gap表示有序数组的长度(1,2,4,8……) for(int gap = 1; gap < len; gap*=2){ int i; // 将"每2个相邻的子数组" 进行合并排序。 for(i = 0; i+2*gap-1 < len; i+=(2*gap)){ merge(arr, i, i+gap-1, i+2*gap-1); } // 若 i+gap-1 < len-1,则剩余一个子数组没有配对。 // 将该子数组合并到已排序的数组中。 if (i+gap-1 < len-1){ merge(arr, i, i+gap-1, len-1); } } } } //两路归并算法,两个排好序的子序列合并为一个子序列 public static void merge(int []arr, int left, int mid, int right){ int []tmp=new int[arr.length];//辅助数组 int p1=left,p2=mid+1,k=left;//p1、p2是检测指针,k是存放指针 while(p1<=mid && p2<=right){ if(arr[p1]<=arr[p2]) tmp[k++]=arr[p1++]; else tmp[k++]=arr[p2++]; } while(p1<=mid) tmp[k++]=arr[p1++];//如果第一个序列未检测完,直接将后面所有元素加到合并的序列中 while(p2<=right) tmp[k++]=arr[p2++];//同上 //复制回原素组 for (int i = left; i <=right; i++) arr[i]=tmp[i]; } public static void main(String[] args){ int[] arr = { 49, 38, 65, 97, 76, 13, 27, 50 }; //mergeSortUp2Down(arr, 0, a.length-1); mergeSortDown2Up(arr); System.out.println("排好序的数组:"); for (int e : arr) System.out.print(e+" "); } }

