数据结构与算法系列——排序(8.1)_冒泡排序
1. 工作原理（定义）
核心思想：冒泡排序是一种典型的 交换排序 ，通过比较相邻元素大小来决定是否交换位置
冒泡排序的思想：不停地比较相邻的两个记录，如果相邻的两个记录的次序是反序则交换，直到所有的记录都已经排好序了（使关键字最小或最大的记录如气泡一般逐渐往上“漂浮”直至“水面”，所以叫冒泡排序）。
2. 算法步骤
-
比较相邻的元素。如果第一个比第二个大，就交换他们两个。
-
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
-
针对所有的元素重复以上的步骤，除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
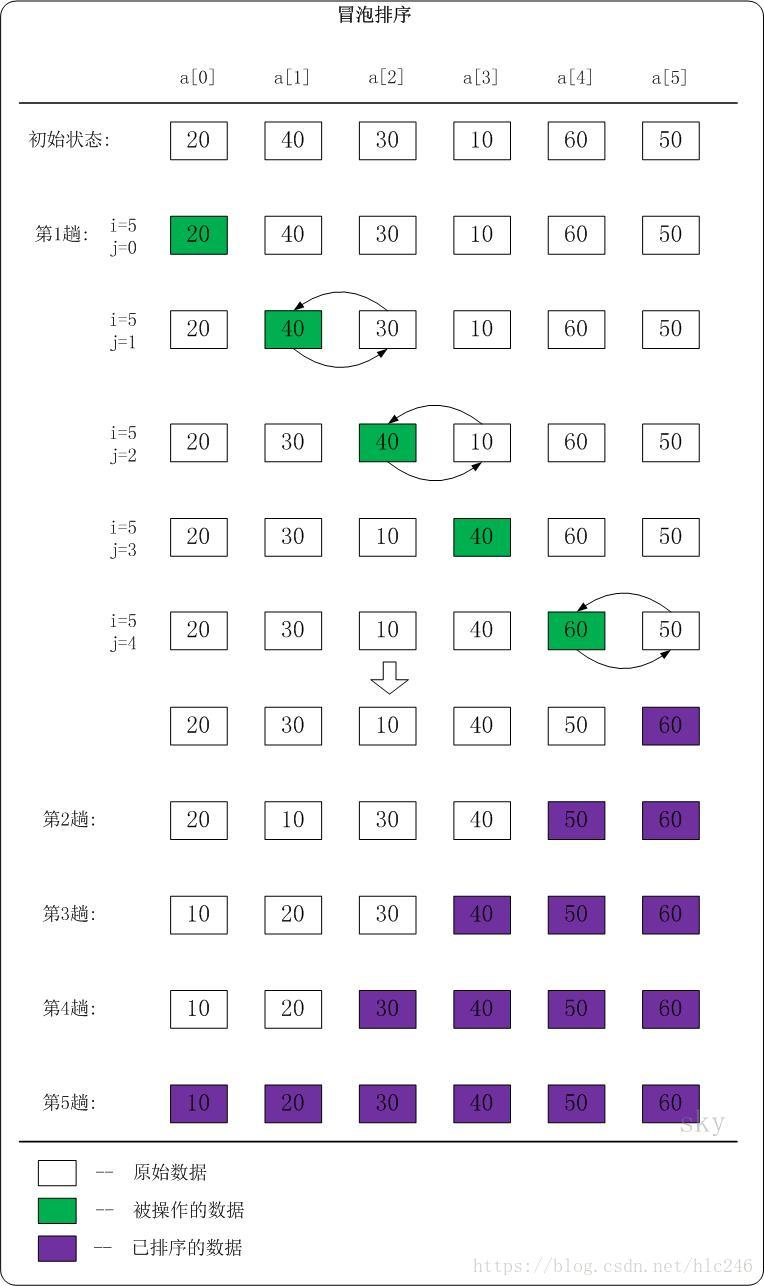
3. 动画演示
4. 性能分析
1. 时间复杂度
（1）顺序排列时，冒泡排序总的比较次数为n-1（比较一轮后就跳出循环），移动次数为0；
（2）逆序排序时，冒泡排序总的比较次数为n(n-1)/2，移动次数为n(n-1)/2次；
（3）当原始序列杂乱无序时，平均时间复杂度为O(n^2)。
若文件的初始状态是正序的，一趟扫描即可完成排序。所需的关键字比较次数 
和记录移动次数 
均达到最小值： 
， 
。所以，冒泡排序最好的时间复杂度为 
。
和记录移动次数 均达到最小值： ， 。所以，冒泡排序最好的时间复杂度为 。 若初始文件是反序的，需要进行 
趟排序。每趟排序要进行 
次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值： 。冒泡排序的最坏时间复杂度为 
。综上，因此冒泡排序总的平均时间复杂度为 。
趟排序。每趟排序要进行 次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值： 。冒泡排序的最坏时间复杂度为 。综上，因此冒泡排序总的平均时间复杂度为 。2. 空间复杂度
冒泡排序排序过程中，Swap函数需要一个临时变量temp进行两两交换，所需要的额外空间为1，因此空间复杂度为O(1)。
3. 算法稳定性
冒泡排序在排序过程中，元素两两交换时，相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。
4. 初始顺序状态
- 比较次数：
- 移动次数：
- 复杂度：
- 排序趟数：
5. 归位
能归位，每一趟排序有一个元素归位。
6. 优点
6. 改进算法
- 对于是否已经是有序排列进行判断；
- 对已经排序好的元素不参与重复的比较。
7. 具体代码
public int[] bubbleSort1(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝，不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
for (int i = 1; i < arr.length; i++) {
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {//等于就不交换，保证了稳定性
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
return arr;
}
/*
*设置一个标识，如果在某一趟遍历中没有发生交换，说明排序已经完成，即算法完成
*/
public int[] bubbleSort2(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝，不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
for (int i = 1; i < arr.length; i++) {
// 设定一个标记，若为true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已经完成。
boolean flagChange = true;
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flagChange = false;
}
}
if (flagChange) {
break;
}
}
return arr;
}
// set flag to indicate what next step should begin from
public int[] bubbleSort3(int[] sourceArray) {
// 对 arr 进行拷贝，不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int tmpNextPosition = sourceArray.length-1;
for (int i = 1; i < arr.length; i++) {
// 设定一个标记，若为true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已经完成。
boolean flagChange = true;
int nextPosition = tmpNextPosition;
for (int j = 0; j < nextPosition; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flagChange = false;
tmpNextPosition = j;
}
}
if (flagChange) {
break;
}
}
return arr;
}
