数据结构与算法系列——排序(7)_堆排序
1. 工作原理(定义)
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
- 大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
- 小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
2. 算法步骤
-
创建一个最大堆 H[0……n-1];
-
把堆首(最大值)和堆尾互换;
-
把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
-
重复步骤 2,直到堆的尺寸为 1。
创建最大堆(Build-Max-Heap)的作用是将一个数组改造成一个最大堆,,接受数组和堆大小两个参数,Build-Max-Heap 将自下而上的调用 Max-Heapify 来改造数组,建立最大堆【注意从非叶子节点开始】。因为 Max-Heapify 能够保证下标 i 的结点之后结点都满足最大堆的性质,所以自下而上的调用 Max-Heapify 能够在改造过程中保持这一性质。

堆排序(Heap-Sort)是堆排序的接口算法,Heap-Sort先调用Build-Max-Heap将数组改造为最大堆,然后将堆顶和堆底元素交换,之后将底部上升,最后重新调用Max-Heapify保持最大堆性质【因为 Max-Heapify 能够保证下标 i 的结点之后结点都满足最大堆的性质,所以自下而上的调用 Max-Heapify 能够在改造过程中保持这一性质。】。由于堆顶元素必然是堆中最大的元素,所以一次操作之后,堆中存在的最大元素被分离出堆,重复n-1次之后,数组排列完毕。整个流程如下:

3. 动画演示

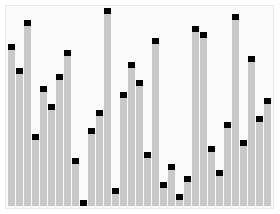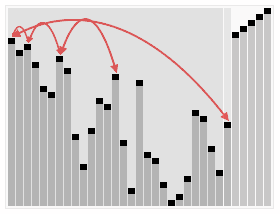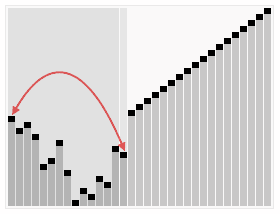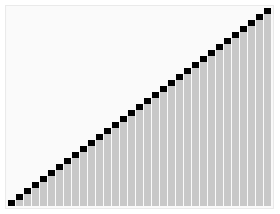
4. 性能分析
1. 时间复杂度
堆排序的时间等于建堆和进行堆调整的时间。
构建最大堆大概需进行n/2 * 2 = n次比较和n/2次交换,故时间复杂度为O(n)。
堆调整的时间为(n - 1)*O(log2(n))。
堆排序的时间复杂度为O(n*logn)。
在最优、最坏和平均情况下,其时间复杂度为 O(n*logn)。
2. 空间复杂度
堆排序为就地排序,因此空间复杂度为O(1)。
3. 算法稳定性
堆排序是不稳定的算法,在构建堆过程中元素的顺序可能会发生变化。
4. 初始顺序状态
- 比较次数:
- 移动次数:
- 复杂度:
- 排序趟数:
5. 归位
能归位,每一趟排序有一个元素归位。
6. 优点
6. 具体代码
import java.util.Arrays; public class HeapSort { public static void main(String[] args) { int [] array = new int[]{2,3,5,6,7,8,23,1,9}; array = heapSort(array); for (int i = 0; i < array.length; i++) { System.out.print(array[i]+" "); } } // 堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算 public static int[] heapSort(int[] sourceArray) { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); int len = arr.length; // 建立最大堆 buildMaxHeap(arr, len); // 首尾元素交换,长度减一,尾部元素最大 for (int i = len - 1; i > 0; i--) { swap(arr, 0, i); len--; heapify(arr, 0, len); } return arr; } /** * 创建最大堆(Build-Max-Heap)的作用是将一个数组改造成一个最大堆,接受数组和堆大小两个参数, * Build-Max-Heap 将自下而上的调用 Max-Heapify 来改造数组,建立最大堆【注意从非叶子节点开始】。 * 因为 Max-Heapify 能够保证下标 i 的结点之后结点都满足最大堆的性质,所以自下而上的调用 Max-Heapify 能够在改造过程中保持这一性质。 */ private static void buildMaxHeap(int[] arr, int len) { // 非叶子节点开始 for (int i = (int) Math.floor(len / 2); i >= 0; i--) { heapify(arr, i, len); } } // 最大堆调整(Max Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点 private static void heapify(int[] arr, int i, int len) { int left = 2 * i + 1; int right = 2 * i + 2; int largest = i; if (left < len && arr[left] > arr[largest]) { largest = left; } if (right < len && arr[right] > arr[largest]) { largest = right; } if (largest != i) {//保证下标 i 的结点之后结点都满足最大堆的性质 swap(arr, i, largest); heapify(arr, largest, len); } } private static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }

