数据结构与算法系列——排序(2)_直接插入排序
1. 工作原理(定义)
直接插入排序(Straight Insertion Sort)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,将它插入到有序表中的适当位置,使之成为新的有序表,重复n-1次可完成排序过程。
【通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。】
2. 算法步骤
设数组为a[0…n]。
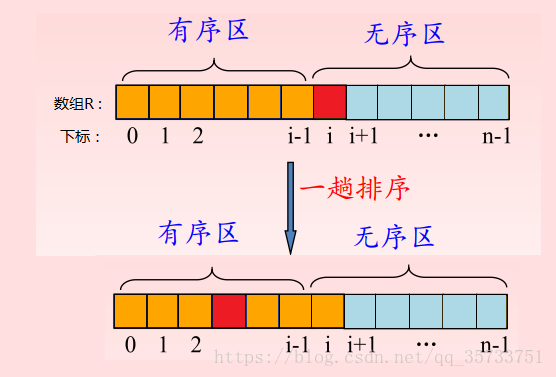
1. 将原序列分成有序区和无序区。a[0…i-1]为有序区,a[i…n] 为无序区。(i从1开始)
2. 从无序区中取出第一个元素,有序区中从后向前扫描查找要插入的位置索引j。
3. 将a[j]到a[i-1]的元素后移,并将a[i]赋值给a[j],使R[0 … i]变为新的有序区。【增量法】
4. 重复步骤2~3,直到无序区元素为0。
3. 动画演示
1. 最好的情况
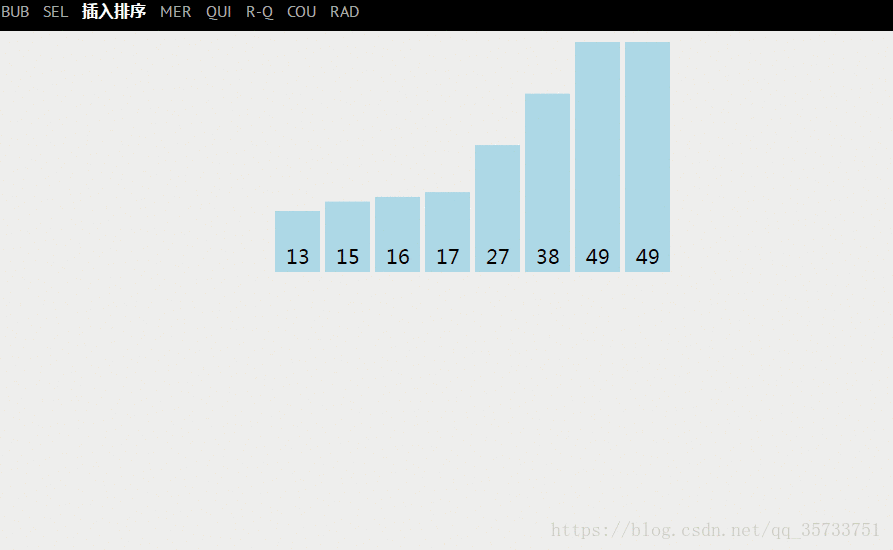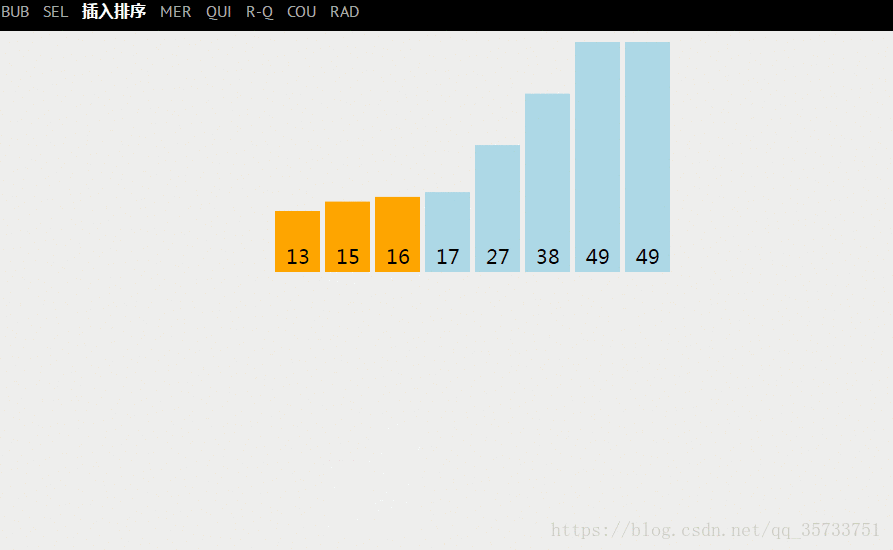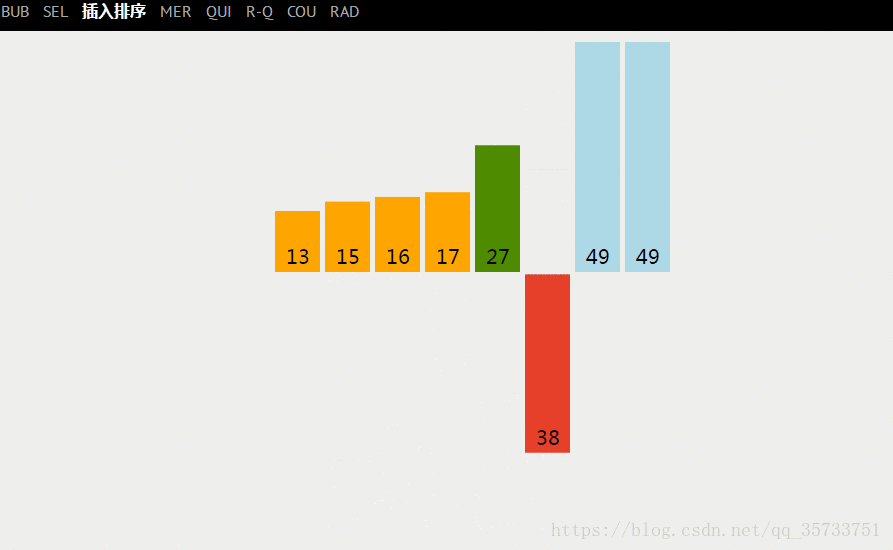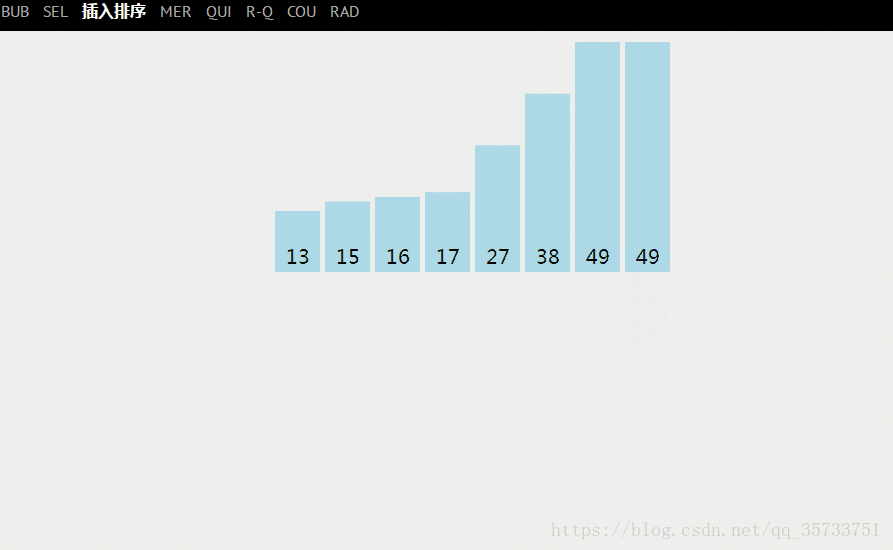
最好的情况就是,待排关键字序列的顺序本身就是有序的(即从小到大的方式排列),这样的话,在排序进行比较的时候每次只比较一次就行了,那么总的“比较”次数为:n-1。【![]() 】
】
在直接插入排序算法中每次都需要提取无序区中的关键字,即tmp=R[i];同时还需要把关键字插入到有序区中合适的位置,即R[j].key = temp.key 。那么总的移动次数为:2(n−1)。
因此在最好的情况下,直接插入排序算法的时间复杂度是:O(n)。
2. 最坏的情况
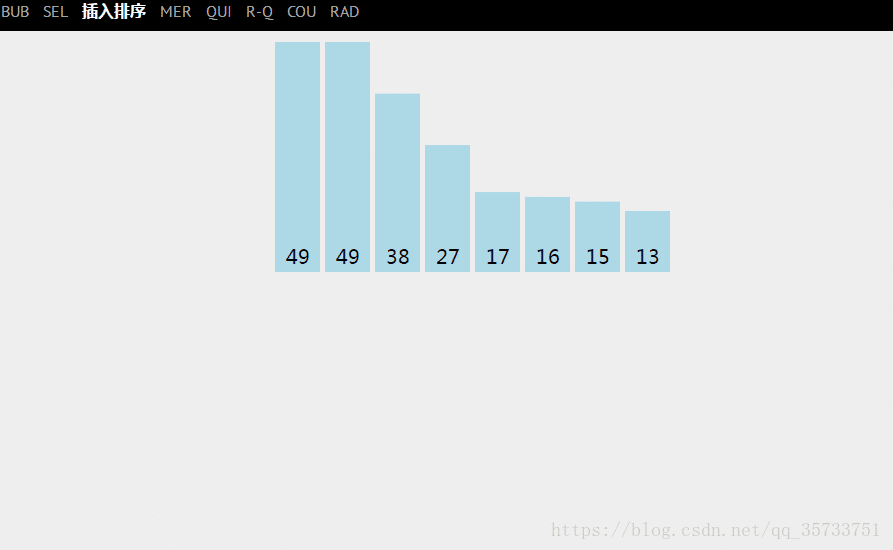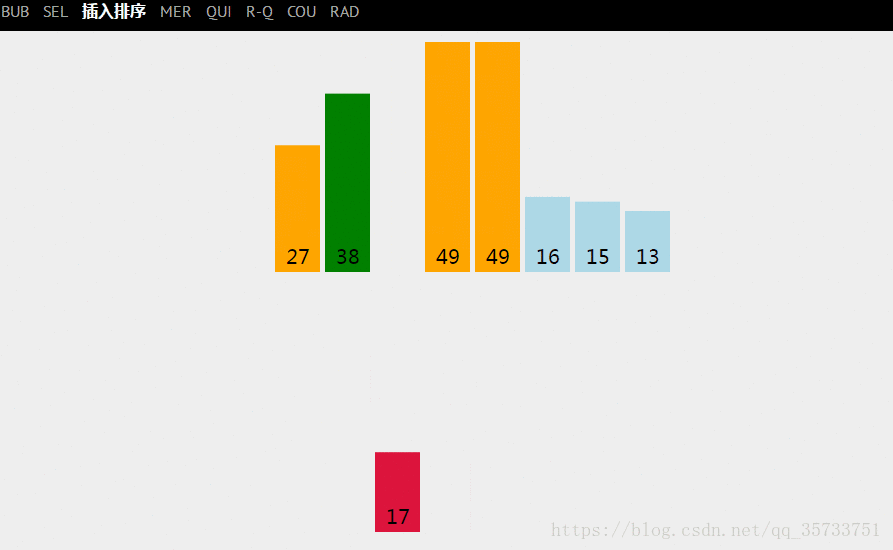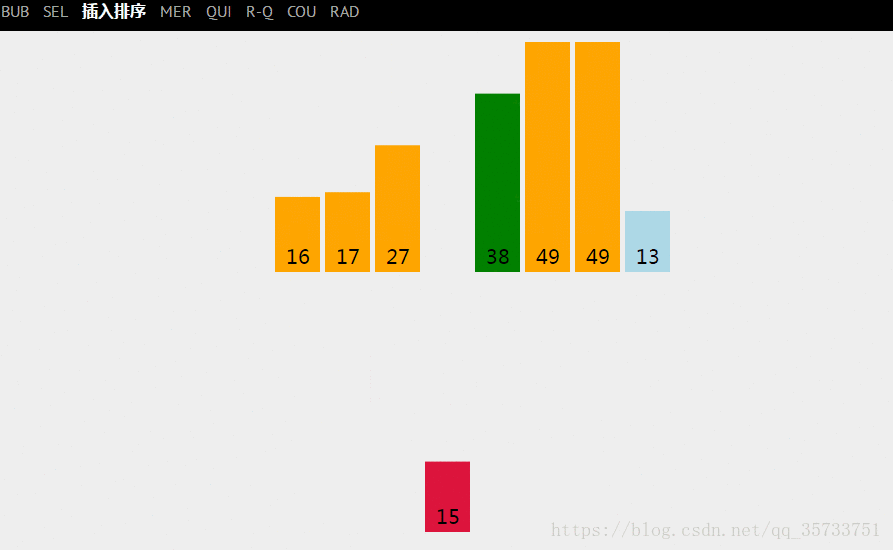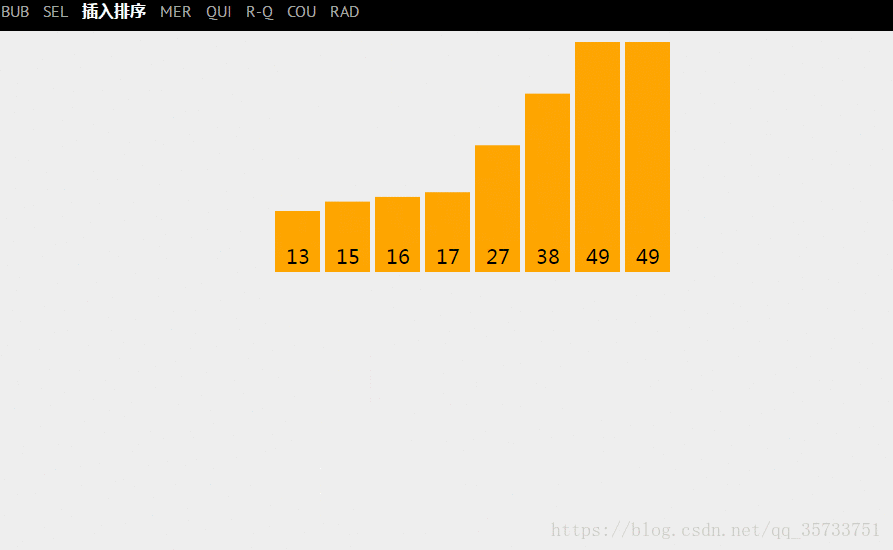
对于最坏的情况就是,我们的需求是按从小到大的方式排序,但是关键字序列中的顺序是逆序的(即从大到小的方式排列),在这种情况下,每次都要把有序区中的所有关键字都比较一次,总的比较次数为: n(n−1)/2。【![]() 】
】
在最坏的情况下,每次都要把关键字插入最前面的位置(即每次都要把有序区中所有关键字往后移动),那么总的移动次数为: (n−1)(n+4)/2。【![]() 】
】
因此在最坏的情况下,直接插入排序算法的时间复杂度是O(n^2)。
3. 普通情况

总的平均比较和移动次数大概是:O(n^2)
也就是说,直接插入排序算法的平均时间复杂度还是O(n^2),从稳定性来说,直接插入排序是一个稳定排序。
4. 性能分析
1. 时间复杂度
(1)顺序排列时,只需比较(n-1)次,插入排序时间复杂度为O(n);
(2)逆序排序时,需比较n(n-1)/2次,插入排序时间复杂度为O(n^2);
(3)当原始序列杂乱无序时,平均时间复杂度为O(n^2)。
2. 空间复杂度
插入排序过程中,需要一个临时变量temp存储待排序元素,因此空间复杂度为O(1)。
3. 算法稳定性
插入排序是一种稳定的排序算法。
4. 初始顺序状态
大部分元素有序时较好
- 比较次数:有关
- 移动次数:有关
- 复杂度: 有关
- 排序趟数:无关
4. 归位
不能归为,比如最后一个数为最小值,那么所有的值都未在最终的位置。
5. 优点
- 稳定。
- 相对于冒泡排序与选择排序更快。
- 大部分元素有序时好。
5. 算法改进
1. 二分插入排序(折半插入排序 OR 拆半插入排序),采用折半查找方法。
直接插入排序算法在查找比较的过程中采用的是顺序查找;折半插入排序算法在查找比较的过程中是采用折半查找的,因此折半插入排序的性能略高一些。
2. 希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率,但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
6. 具体代码
import java.util.Arrays;
public class InsertSort{
// 直接插入排序
public int[] insertSort(int[] sourceArray) {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for (int i = 1; i < arr.length; i++) {
// 记录要插入的数据
int tmp = arr[i];
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
while (j > 0 && tmp < arr[j - 1]) {//等于的时候不再减了,保证了稳定性
arr[j] = arr[j - 1];
j--;
}
// 存在比其小的数,插入
if (j != i) {
arr[j] = tmp;
}
}
return arr;
}
}

