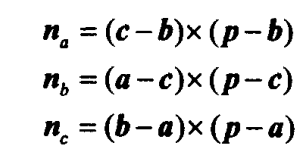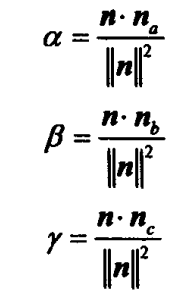重心坐标系

1、图形学把三角形作为基本图形之一(还有点、线)，许多情况下将目标信息存储于顶点结构中由 vertex shader 向下传递到 fragment shader。 vertex shader 每个顶点执行一次，而 fragment shader 每个片元执行一次，并且一个三角形图元的 fragment 多于 vertex (不讨论三角形缩小到片元的情况)，因此需要一个 vertex 目标信息到 fragment 目标信息的映射。为解决问题，插值算法利用重心坐标系来完成工作是众多方法中的一种。

 

2、重心：几何物体的各个部分都受到重力作用，这些重力作用集中于一点，这个点叫几何物体的重心。

 三角形的重心是三条边中线的交点，具有以下性质：

 1)重心到顶点的距离与重心到对边中点的距离为2:1

 2)重心和三角形3个顶点组成的3个三角形面积相等

 3)重心到3个顶点距离的平方和最小

 4)在平面直角坐标系中，重心的坐标是顶点坐标的算术平均

 

3、二维空间笛卡尔坐标系使用向量进行表示的方法：给定一个基点，两个从基点出发的不同向向量。

 1)由二维顶点a、b、c组成的三角形使用向量表示法以a为基点，(b-a) 与 (c-a) 为方向：p = a + β(b -a) + γ(c - a)

 2)化简等式：p = (1 - β - γ)a + βb + γc

 3)添加变量α简化a的系数：α = 1 - β - γ 即有等式：p = αa + βb + γc

 4)对于处于三角形内部的点有α、β、γ的值域为(0.0, 1.0)

 

4、那么在已知p的情况下，要求得重心坐标一般方法

 1)使用β、γ两个位置量得到线性方程进行求解

  2)几何求解，利用长度比的思想，点p从基点a从(c-a)方向上的距离比上(c-a)的距离就是γ，β可以使用相同的方法求得

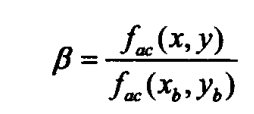
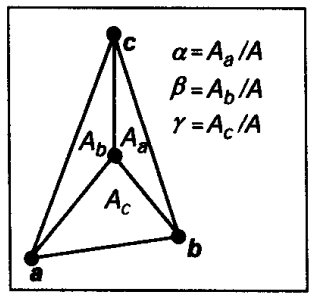
 3)重心坐标与由重心和顶点分割成三个子三角形的面积成正比，所以将每个子三角形的面积比上面积的和即可

  

4、三角形的重心坐标可以扩展到3维后仍然能够使用p = αa + βb + γc，只是等式中的所有顶点都是三维坐标而已，同时这个等式也能够表示一个平面。叉乘能够得到一个平面的法向量，同时叉乘结果的模长的一半能够表示三角  形的面积|AxB| = 0.5*|A||B|sinθ。但是能够看出来，这个面积与二维的不同在于它不带方向的，因此不能直接用于重心坐标系的计算，需要配合点积来判断方向。