先来了解一些基本概念:
1)什么是二叉平衡树?
之前我们了解过二叉查找树,我们说通常来讲, 对于一棵有n个节点的二叉查找树,查询一个节点的时间复杂度为log以2为底的N的对数。
通常来讲是这样的, 但是。。。有例外
比如,我们向一棵树中输入预先排好序的数据, 如1,2,3,4,5,。。。10000, 可以想象到,将形成一棵斜树那么查找10000就要经过9999次比较才能得到,这显然不是我们期望看到的
所以,我们希望引入一个约束条件----任何节点的深度不得过深。
这就是二叉平衡树
二叉平衡树是二叉查找树(排序树)的一种,其每一个节点的左子树和右子树的高度差最多为1
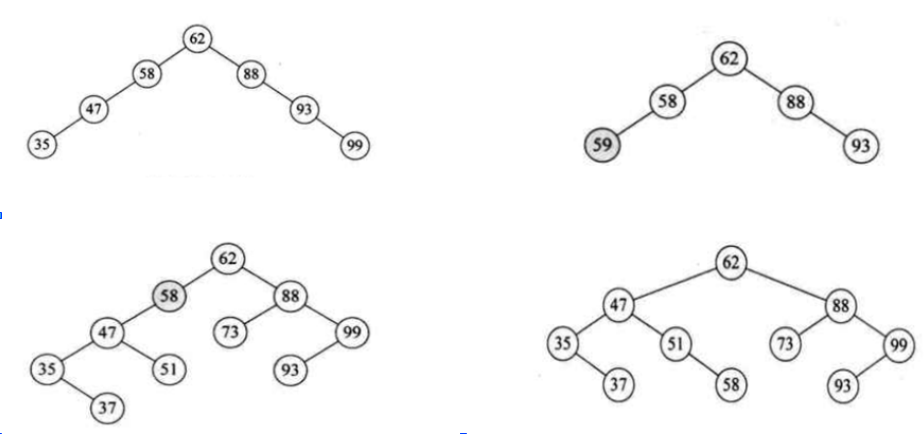
如上图, 左边两棵树并不是二叉平衡树, 因为节点58的左子树和右子树高度差>1。 (分别为2和3)
2)平衡因子?
二叉树上节点的左子树高度 减去 右子树高度, 得到的结果称为该节点的平衡因子
3)最小不平衡树?
当我们给一个二叉平衡树增加新的节点时,会产生最小不平衡树
以 距离插入节点最近的,平衡因子大于1的节点 为根的树, 我们称为最小不平衡树
如
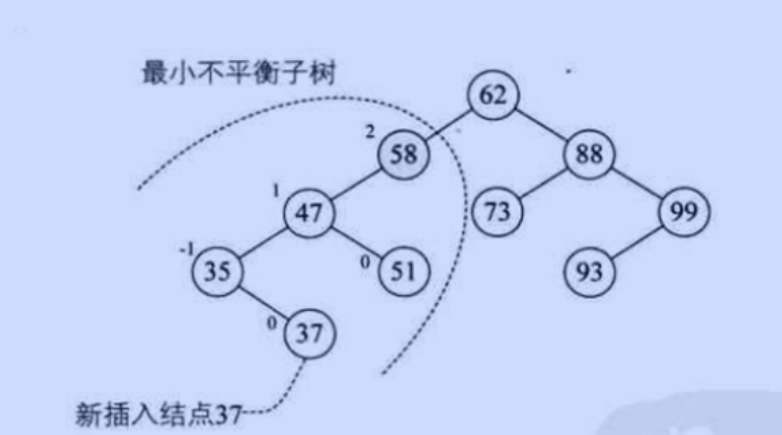
了解了基本概念之后,我们来看看如何构建一棵二叉平衡树
来看一个例子,我们从初始的空AVL树开始插入3,2,1, 当插入1时, AVL的性质在根(3)处被破坏,此时,我们需要在根与其左儿子间实施单旋转以解决这个问题

我们继续插入节点4, 这没什么问题, 但当我们插入节点5时, AVL的性质在节点3处被破坏, 因此, 我们需要在节点3与其右儿子之间实施一次左旋来解决这个问题
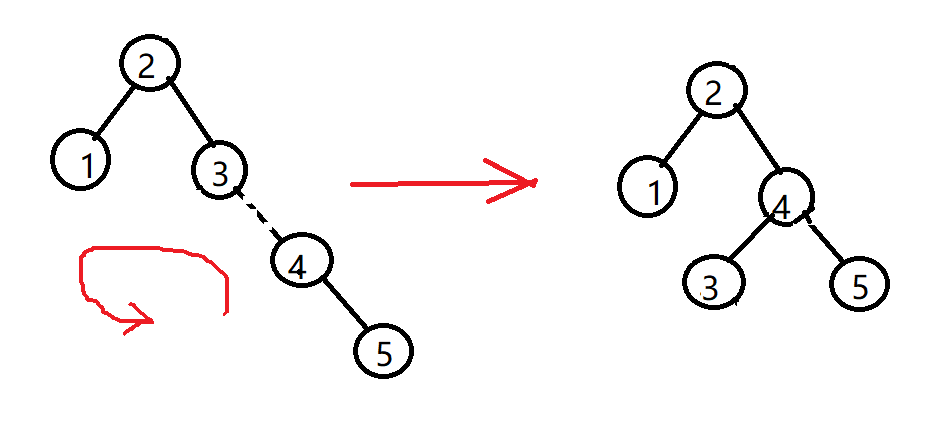
现在我们再插入节点6,此时AVL的性质在根节点(2)处被破坏, 因此我们在根节点和其右节点4之间实施一次左旋
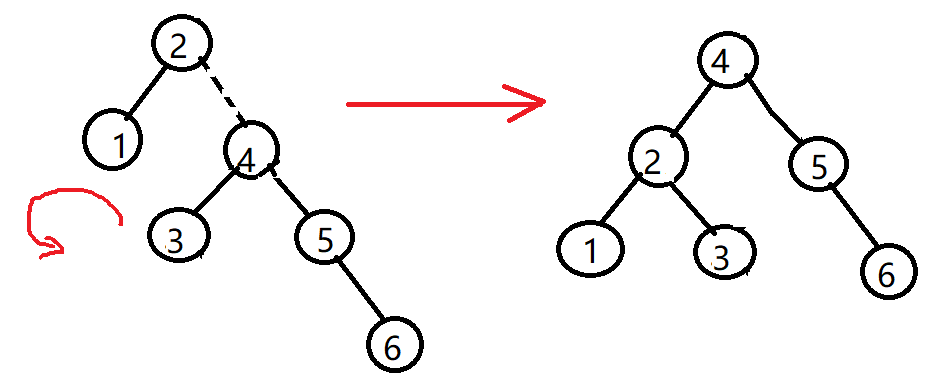
左旋的结果是 4成为根节点,2成为4的左儿子, 4 原本的左儿子3成为2的右儿子
现在再插入节点7, 此时AVL的性质在节点5处被破坏, 因此我们在5节点和其右节点6之间实施一次左旋

根据上面的操作,我们现总结处两条规律:(太绕口,不用记,看图能理解就可以)
假设当我们插入新节点时,导致了原AVL树在节点 p 处不平衡,那么
1)如果添加的新节点是p的左儿子的左儿子, 则在p和其左儿子之间实施一次右旋转, p变成其左儿子的右儿子(如果其左儿子原本已经有右儿子, 则原本的右儿子成为p的左儿子)
2)如果新加的节点是p的右儿子的右儿子, 则在p和其右儿子之间实施一次左旋转,p变成其右儿子的左儿子(如果其右儿子原本已经有左儿子, 则原本的左儿子成为p的右儿子)
感觉头都转晕了😄
but...真正复杂的还在后面。。。。。。。。
现在我们给上面的二叉树插入节点16,这没什么问题, 再插入15, 此时二叉树在节点7处不再平衡,这时我们发现单旋转已经不能解决问题了, 如果只是在7和16之间左旋的话,15将成为16的右节点,这显然不符合二叉排序树的性质。
因此这里我们需要两次旋转,先在15和16之间进行一次右旋,右旋之后就满足了上文规律2)的条件,此时再进行一次左旋
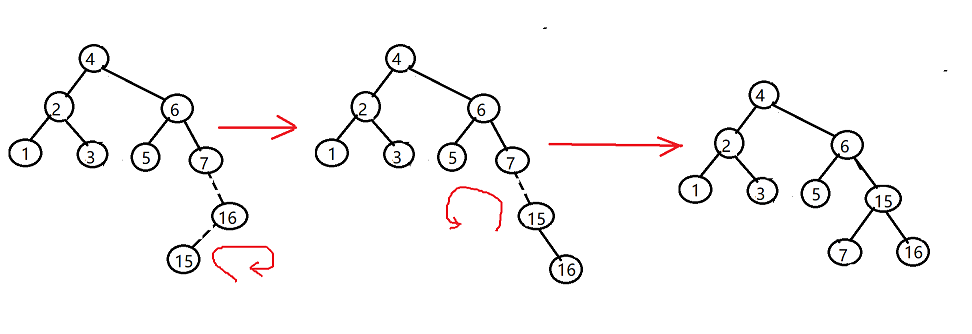
现在我们再插入14, 跟上面情况类似,插入之后需要执行先右旋再左旋的操作
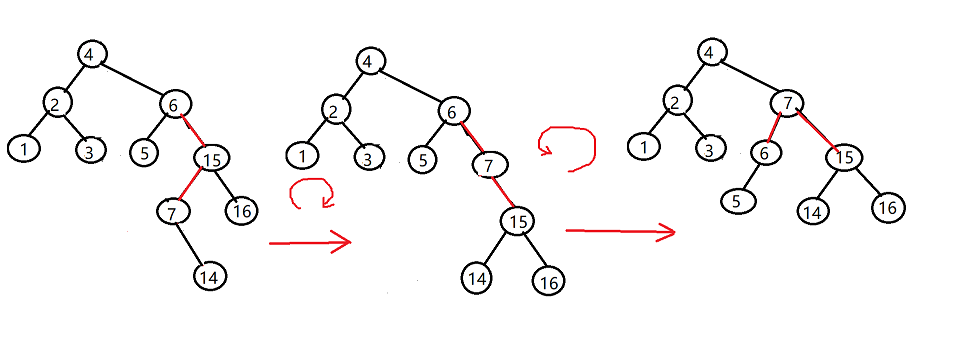
现在让我们再做个小结,
当我们插入新节点时,导致了原AVL树在节点 p 处不平衡,那么
3)如果添加的新节点是p的右儿子的左儿子, 则先在其右儿子和右儿子的左儿子之间实施一次右旋转, 再在p和其右儿子之间实施一次左旋转
3)如果添加的新节点是p的左儿子的右儿子, 则先在其左儿子和左儿子的右儿子之间实施一次左旋转, 再在p和其左儿子之间实施一次右旋转
再高度总结下: 同向时单旋转,异向时双旋转
原理就到这里了, 代码实现比较复杂,这里就不再写了,个人觉得没有必要,因为AVL树是最古老的平衡树, 我们了解其原理是为了下一步----更好的理解红黑树。




