哈夫曼树通常用于压缩, 先看下哈夫曼树的由来


看上面这段代码, 结合右图中各个分数段的比例。 现在假设一共有100个学生, 那么一共要执行多少次判断的逻辑呢?
显然 5 + 15*2 + 40*3 + 30*4 +10*5 = 325次
那么是否可以优化呢?----当然也是可以的, 我们如果把分数占比大的判断往前放, 总的判断次数就可以减小
如 if (a<80){
}else if(a<90){
}else if (a<70){
}else if (a<100){
}else{
}
那么总的判断执行次数就变成了 40 + 30*2 + 15*3 + 10*4 + 5*5 = 210次, 当然,这是一段伪代码, 只是体现性能上的提升
现在我们把上面两段代码分别转换成树
这里引入一个概念叫做树的路径
哈夫曼大叔说,从树中一个节点到另一个节点之间的分支,构成两个节点之间的路径,路径上的分支数目称为路径长度。
树的路径长度就是树根到每一个节点的路径长度之和
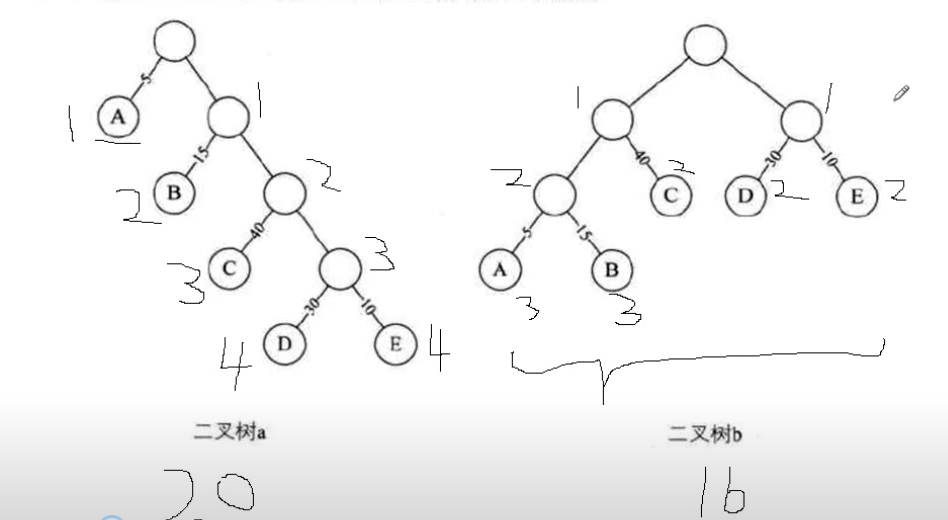
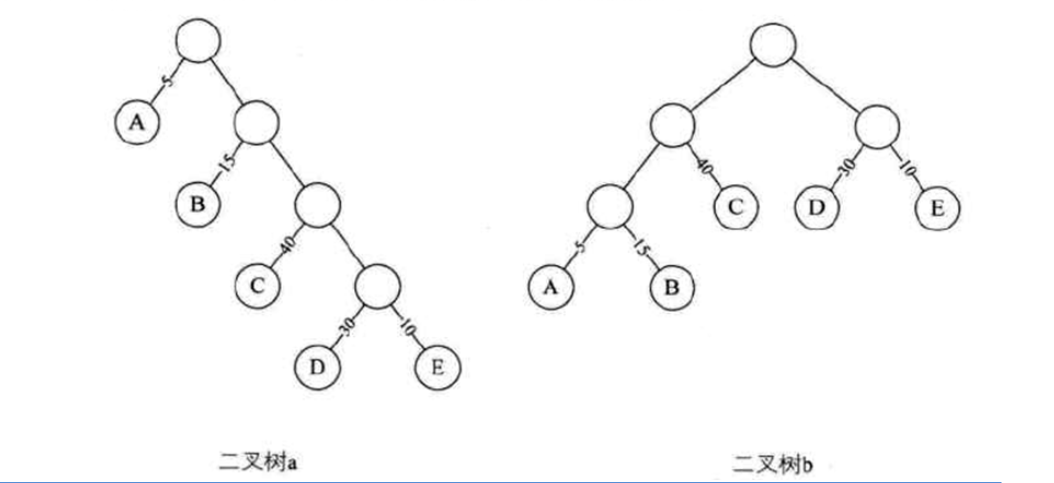
如图, 二叉树a的路径长度为20, 二叉树b的路径长度为16
上图中5,15,40...这些称为节点的权值
节点的带权路径长度 为节点的路径长度与该节点权值的乘积, 如二叉树a中, 节点D的带权路径长度为4*30 = 120
树的带权路径长度 为树中所有叶子节点的带权路径之和, 如二叉树a的带权路径长度为: 1*5 + 2*15 + 3*40 +4*30 +4*10 = 315
二叉树b的带权路径长度为:3*5+3*15+2*40+2*30+2*10 = 220
对于一棵有n个叶子节点的二叉树, 我们可以随意组合出很多种, 其中带权路径长度最小的二叉树称为哈夫曼树
那么下一步,如何构造一棵哈夫曼树呢?
1)先把有权值的叶子节点按照权值从小到大的顺序排成一个有序序列
A5 E10 B15 D30 C40
2)取最小的两个叶子作为节点N1的子节点, 注意较小的为左儿子,新节点的权值为两个子节点的权值之和
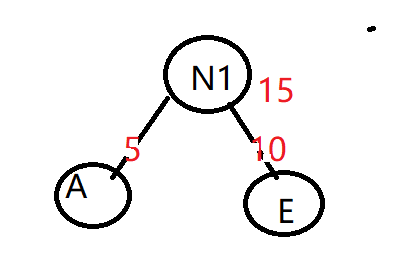
3)用N1替换A和E,插入有序序列中, 保持从小到大排序,即N15 B15 D30 C40
4) 重复步骤2), 将N1和B作为新节点N2的子节点,较小的为左儿子,新节点的权值为两个子节点的权值之和
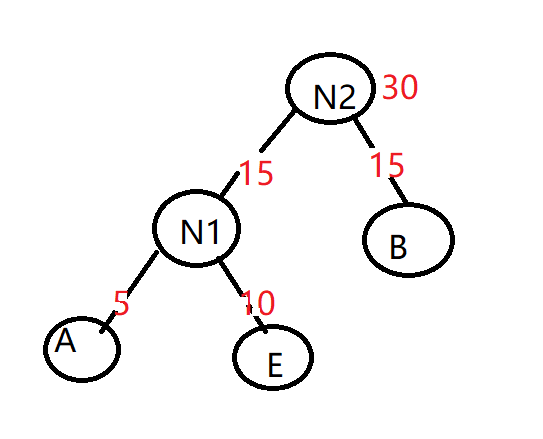
5)用N2替换N1和B,插入有序序列中, 保持从小到大排序,即N30 D30 C40
6)重复步骤2),将N2和D作为新节点N3的子节点
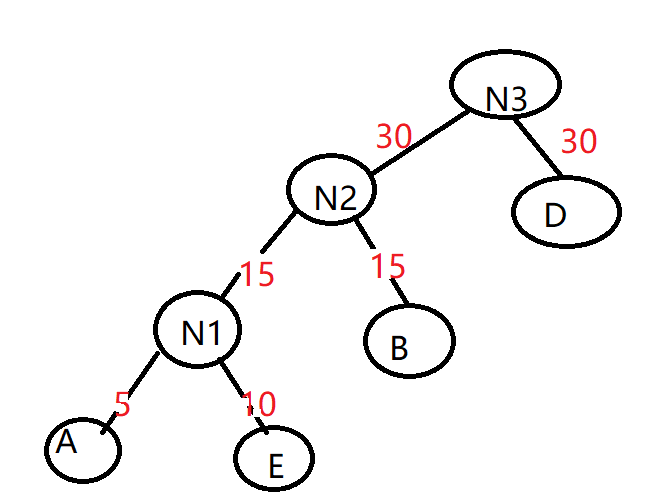
7)用N3替换N2和D, 插入有序序列中, 保持从小到大排序,即C40 N60
8)因为只剩最后两个元素, 因此C40和N60成为新节点T的子节点,T即为根节点
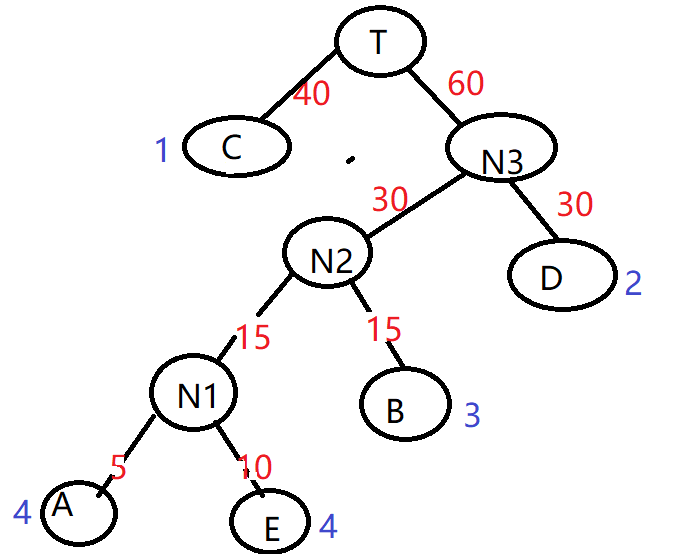
上图即构造了一棵哈夫曼树,
它的带权路径长度为 1*40 + 2*30 + 3*15 +4*5 +4*10 = 205
小结: 构建哈夫曼树的一般过程:
首先把叶子节点排成排成有序序列,
然后取最小的两个构建树叶, 用他们的和值构建他们的父节点,
把父节点放到序列中,再重复上面的步骤
接下来我们看看代码实现:
首先定义节点内部类:
1 /** 2 * 定义节点 3 */ 4 public static class TreeNode implements Comparable<TreeNode>{ 5 //数据域 6 String data; 7 //权值 8 int balance; 9 //父节点 10 TreeNode parent; 11 //左儿子 12 TreeNode leftChild; 13 //右儿子 14 TreeNode rightChild; 15 16 //比较权值 17 @Override 18 public int compareTo(TreeNode treeNode) { 19 if(balance < treeNode.balance){ 20 return 1; 21 }else { 22 return -1; 23 } 24 } 25 26 public TreeNode(String data, int balance){ 27 this.data = data; 28 this.balance = balance; 29 this.parent = null; 30 this.leftChild = null; 31 this.rightChild = null; 32 } 33 }
然后构造方法:
1 //根节点 2 private TreeNode root; 3 4 public HuffmanTree(TreeNode root){ 5 this.root = root; 6 }
创建树:
1 /** 2 * 构建哈夫曼树 3 * @param list 4 * @return 5 */ 6 public static HuffmanTree createHuffmanTree(ArrayList<TreeNode> list){ 7 while(list.size() > 1){ 8 //首先对list进行排序 9 //因为我们给TreeNode实现了compareTo, 所以会按照权值来排序 10 Collections.sort(list); 11 //取出最小的两个节点 12 TreeNode firstNode = list.get(list.size()-1); 13 TreeNode secondNode = list.get(list.size()-2); 14 //创建一个新节点, 权值为前两个节点的权值之和 15 TreeNode newNode = new TreeNode("N", firstNode.balance + secondNode.balance); 16 newNode.leftChild = firstNode; 17 newNode.rightChild = secondNode; 18 firstNode.parent = newNode; 19 secondNode.parent = newNode; 20 //用新节点替换刚取出的最小节点 21 list.remove(firstNode); 22 list.remove(secondNode); 23 list.add(newNode); 24 } 25 //while循环执行完之后, list中只剩下最后一个节点, 这个节点就是根节点 26 return new HuffmanTree(list.get(0)); 27 }
树的遍历
1 /** 2 * 哈夫曼树的遍历 3 */ 4 public void showHuffmanTree(){ 5 //这里利用了队列 先进先出 的特点 6 LinkedList<TreeNode> list = new LinkedList<>(); 7 //根节点入队 8 list.offer(root); 9 while(list.size()>0){ 10 //取出来一个 11 TreeNode node = list.pop(); 12 //打印出来 13 System.out.println(node.data+"("+node.balance+")"); 14 //子节点入队 15 if (node.leftChild != null){ 16 list.offer(node.leftChild); 17 } 18 if (node.rightChild != null){ 19 list.offer(node.rightChild); 20 } 21 } 22 }
测试代码:
1 @Test 2 fun testHuffmanTree(){ 3 val list = arrayListOf( 4 HuffmanTree.TreeNode("A", 5), 5 HuffmanTree.TreeNode("B", 15), 6 HuffmanTree.TreeNode("C", 40), 7 HuffmanTree.TreeNode("D", 30), 8 HuffmanTree.TreeNode("E", 10) 9 ) 10 11 val tree = HuffmanTree.createHuffmanTree(list) 12 tree.showHuffmanTree() 13 }
测试结果
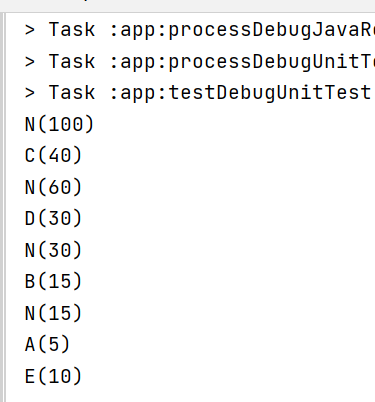
哈夫曼编码:
哈夫曼编码的目的是数据压缩
比如ABCDEF的二进制表示如下

此时假设我们要存储ABCDE, 则计算机存储的是000001010011100 共15个字符
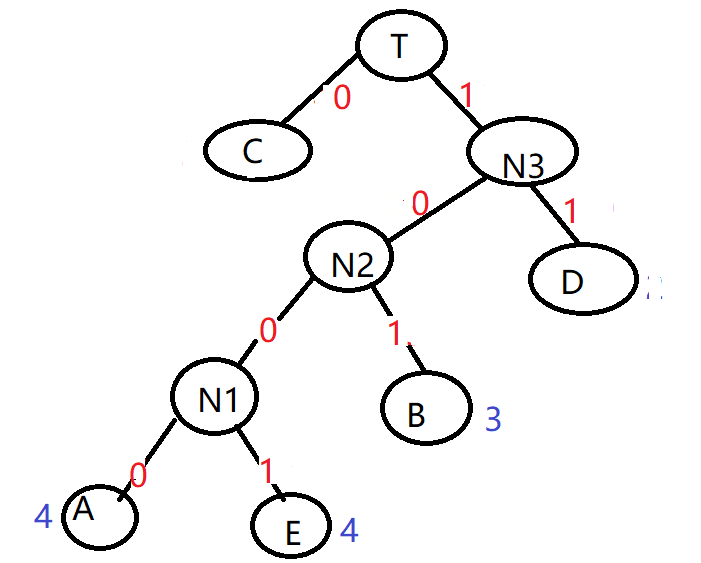
那么我们在哈夫曼树中,将节点的左路径权值用0替换,右路径用1替换,则得到下图
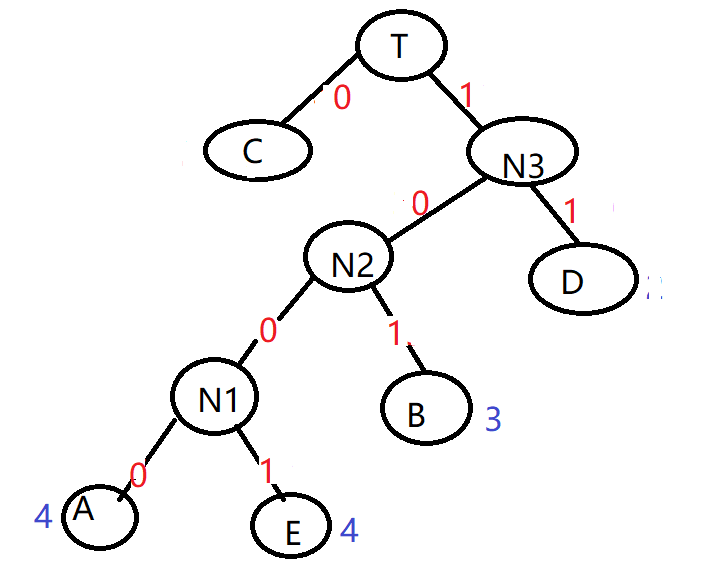
那么A=1000 B=101 C=0 D=11 E=1001
此时存储ABCDE,则计算机存储10001010111001共14个字符
好像没什么大变化是吧?😄
这是因为我们没有引入权值,我们知道哈夫曼树是基于权值来构建的, 回到本文最开始的例子
假设一共100个数字, A出现5次,B出现15次,C出现40次,D出现30次, E出现10次, 那么按照正常编码, 计算机存储这100个ABCDE共计需要100*3 = 300个字符
但是如果用哈夫曼编码, 则只需要存储 4*5 + 3*15 +1*40 + 2*30 + 4*10 = 205 个字符
节约了31.6%的存储空间




