从零开始学算法---归并排序（后序遍历）

如果有这样一个数组，整体是无序的， 但是前半部分和后半部分分别是有序的

 

 

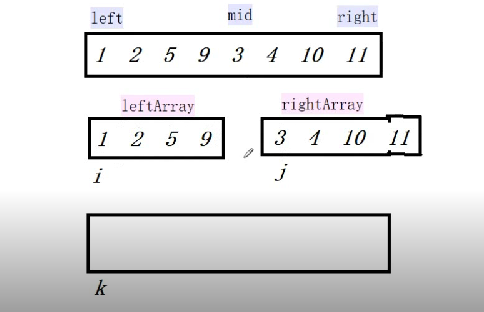
 现在我们定义一个方法对它进行排序：

/**
     * array 如： intArrayOf(1,2,5,9,3,4,10,11)
     * left = 0,
     * middle = 4,
     * right = 7
     */
    fun merge(array: IntArray, left: Int, middle: Int, right: Int){
        //我们先把数组按照Middle分割成两个数组
        val leftArraySize = middle-left
        val rightArraySize = right-middle+1
        //定义两个数组 (这就是归并排序消耗空间的地方)
        val leftArray = IntArray(leftArraySize)
        val rightArray = IntArray(rightArraySize)
        //把原数组的元素copy到新数组
        for (i in left until middle) {
            leftArray[i - left] = array[i]
        }
        for (i in middle..right) {
            rightArray[i - middle] = array[i]
        }

        //合并
        var i=0
        var j=0
        var k=left
       while (i < leftArraySize && j < rightArraySize){
           //如果左边第一个数比右边第一个数小
           if (leftArray[i] < rightArray[j]){
               array[k] = leftArray[i]
               k++
               i++
           } else {
               array[k] = rightArray[j]
               k++
               j++
           }
       }
        //上面while会在某个数组元素取完之后执行完毕
        //如果 i 小于 leftArray.size, 说明左边数组中有元素没取完
        while (i<leftArraySize){
            //那么就把左边数组中的元素放到array中
            array[k++] = leftArray[i++]
        }
        //如果  j小于 rightArray.size, 说明右边数组中有元素没取完
        while (j<rightArraySize){
            //那么就把右边数组中的元素放到array中
            array[k++] = rightArray[j++]
        }
    }

定义归并排序的方法

fun mergeSort(array: IntArray, start: Int, end: Int){
        if (start==end){
            return
        }else{
            //取中间值
            val middle = (start+end)/2
            //对左边归并排序
            mergeSort(array, start, middle)
            //右边归并排序
            mergeSort(array, middle+1, end)
            //左右合并
            merge(array, start, middle+1, end)

        }
    }

这里不是很好理解

 

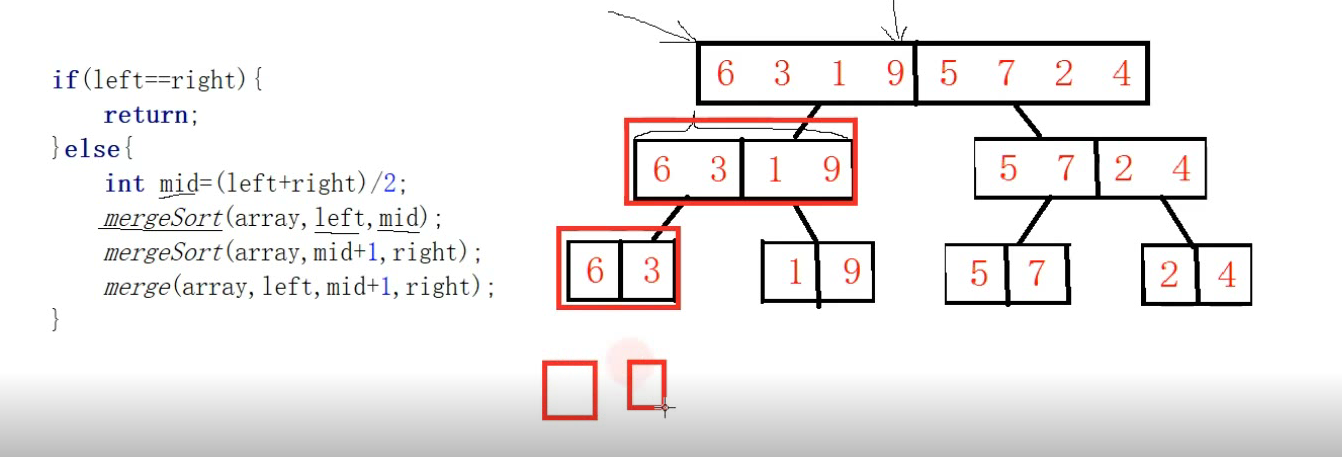
 要理解这段代码需要先理解递归进栈出栈的顺序

结合上图， 代码执行到mergeSort(array, left, mid)的时候，递归调用自身，同时后面的两行代码进栈

递归调用又得到Mid为之前的一半， 再递归调用自身， 同时后面两行进栈

直到left==right，第一层递归调用完毕。代码按照先进后出的原则出栈，可以想象最先被执行到的是6和3的merge, 然后才是3,6 和1,9的合并， 最后执行1,3,6,9,和2,4,5,7的合并。

所以不难理解，归并排序的时间复杂度也是n*log2N

 

其实就是使用递归将数组拆分成一个一个的元素， 然后从下往上两两合并