从零开始学算法---二叉树

什么是树？ 

树是n(n>=0)个结点的有限集。n=0时称为空树，在任意一棵非空树中，有且仅有一个特定的称为根(root)的结点， 当n>1时，其余结点可分为m个互不相交的有限集。 下图中第一张图就不是树， 因为d和e相交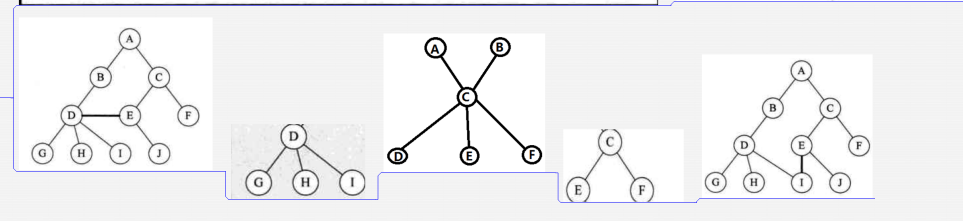

 

 

树的存储结构？

树的存储结构一般有4种，

1）双亲表示法，就是在每个节点中标示出它的父节点

 

 

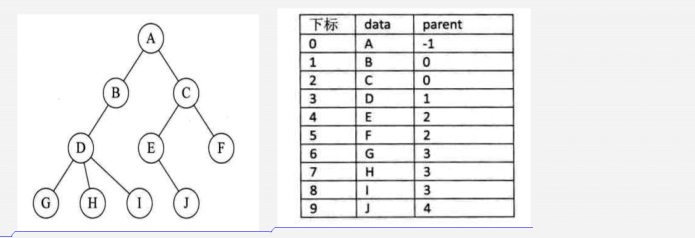
 2）孩子表示法，每个节点携带指针位指向自己的孩子

 

 

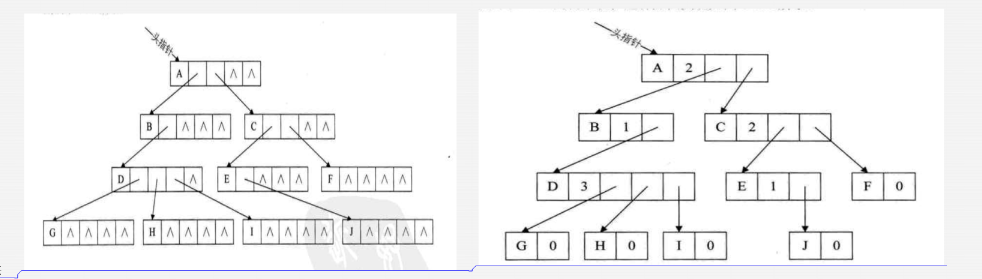
 这种方法中，每个节点除了数据域外，还要额外携带m个指针位（m为树的度）

3）双亲孩子表示法

 

 

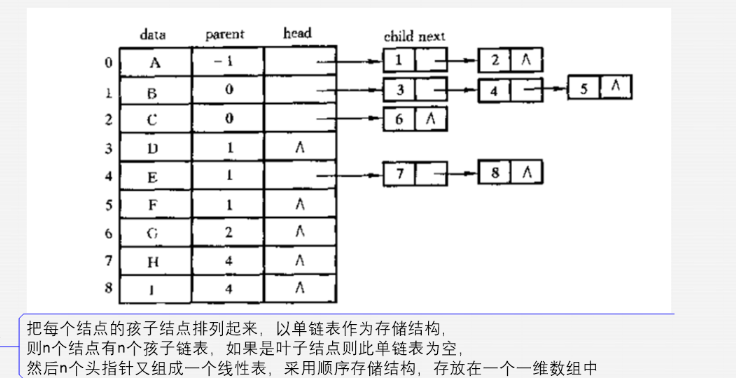
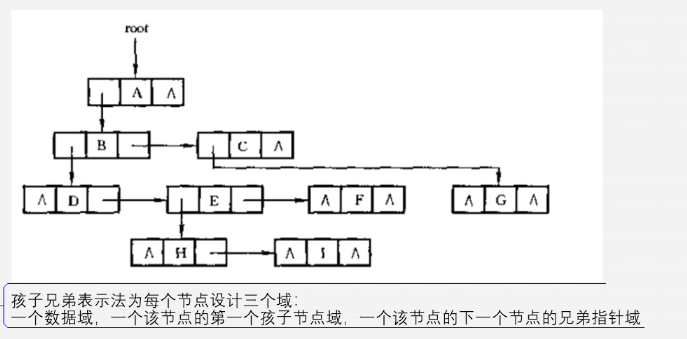
 4），孩子兄弟表示法

 

 

 二叉树？

度<=2的树称为二叉树

二叉树的存储结构？

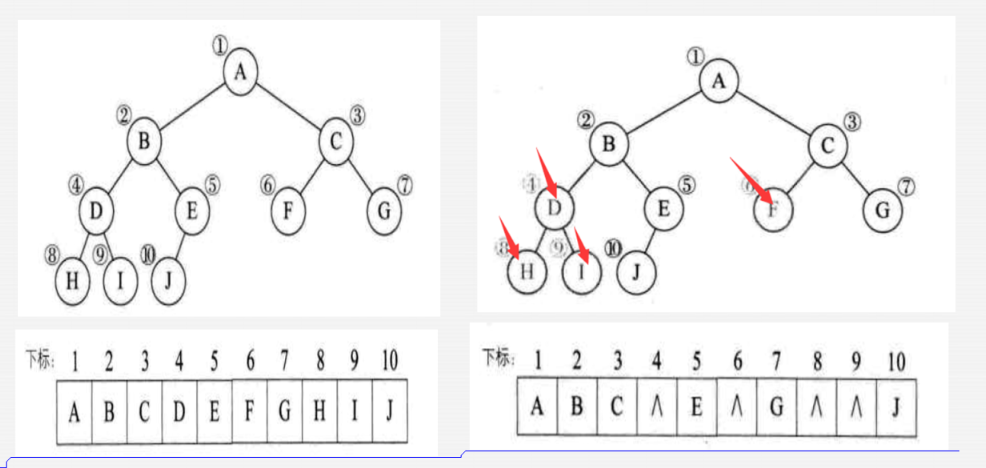
1）顺序存储

 

 

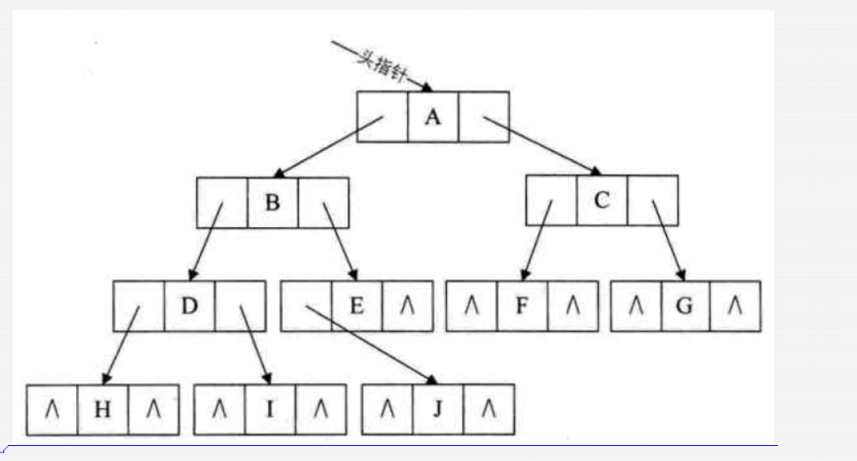
 2， 链式存储（使用孩子表示法）

 

 

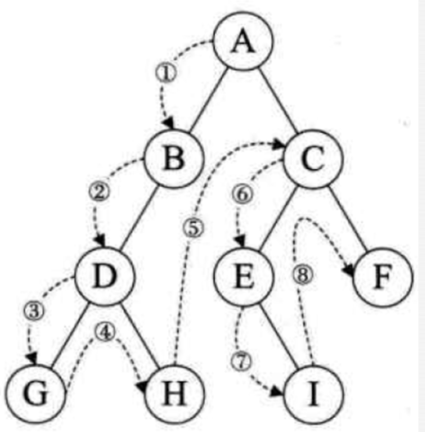
 二叉树的遍历？

1）前序遍历（DLR）， 规则是：若二叉树为空，则空操作返回，否则先访问根节点，然后前序遍历左子树，再前序遍历右子树

 

 

 代码实现：

public class BinaryTree<E>{
    /**
     * 节点内部类
     * 这里我们用孩子表示法
     * 因此需要定义一个数据域和两个指针域
     */
    class Node<E>{
        private E data;
        private Node<E> leftChild;
        private Node<E> rightChild;
        
        public Node(E data, Node<E> leftChild, Node<E> rightChild) {
            this.data = data;
            this.leftChild = leftChild;
            this.rightChild = rightChild;
        }
    }
    
    //root节点
    Node<E> root;

    /**
     * 为了便于测试，我们在构造方法里生成一颗二叉树
     * @param root
     */
    public BinaryTree(E root) {
        this.root = new Node(root, null, null);
        createBinaryTree();
    }
    
    /**
     * 创建一颗二叉树
     */
    private void createBinaryTree() {
        //创建节点
        Node<E> nodeB = new Node("B",null, null );
        Node<E> nodeC = new Node("C",null, null );
        Node<E> nodeD = new Node("D",null, null );
        Node<E> nodeE = new Node("E",null, null );
        Node<E> nodeF = new Node("F",null, null );
        Node<E> nodeG = new Node("G",null, null );
        Node<E> nodeH = new Node("H",null, null );
        Node<E> nodeI = new Node("I",null, null );
        //声明节点间的关系，来构建树
        root.leftChild = nodeB;
        root.rightChild = nodeC;
        nodeB.leftChild = nodeD;
        nodeD.leftChild = nodeG;
        nodeD.rightChild = nodeH;
        nodeC.leftChild = nodeE;
        nodeC.rightChild = nodeF;
        nodeE.rightChild = nodeI;
    }
    
    /**
     * 二叉树的前序遍历
     * @param tree
     */
    public void preErgodic(Node<E> root) {
        //如果二叉树为空，则空操作返回
        if(root == null) {
            return;
        }else {
            //否则先访问根节点
            System.out.println(root.data.toString());
            //再前序访问左子树
            preErgodic(root.leftChild);
            //再前序访问右子树
            preErgodic(root.rightChild);
        }
    }
}

测试代码 

public static void main(String[] args) {
        BinaryTree tree = new BinaryTree("A");
        tree.preErgodic(tree.root);
    }

输出结果：

 

 

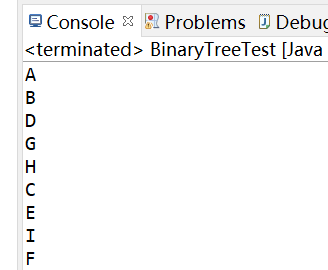
 2）相对于前序遍历(DLR)来说， 中序遍历(LDR)就是先访问左子树，再访问中间节点，再访问右子树

public void middleErgodic(Node<E> root) {
        //如果二叉树为空，则空操作返回
        if(root == null) {
            return;
        }else {
            //否则从根节点开始，先访问左子树
            middleErgodic(root.leftChild);
            //再访问根节点
            System.out.print(root.data.toString() + " ");
            //再访问右子树
            middleErgodic(root.rightChild);
        }
    }

输出结果：

 

 

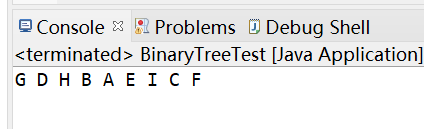
 3）后续遍历（LRD）

public void endErgodic(Node<E> root) {
        //如果二叉树为空，则空操作返回
        if(root == null) {
            return;
        }else {
            //否则从根节点开始，先访问左子树
            endErgodic(root.leftChild);
            //再访问右子树
            endErgodic(root.rightChild);
            //再访问根节点
            System.out.print(root.data.toString() + " ");
        }
    }

输出结果

 

 小结： 所谓前序后序中序其实就是 访问根节点是在访问左右节点的前面、后面还是中间