数据结构与算法(Ⅵ):分治、回溯
分治(divide and conquer)
分治的核心思想是分而治之,即将原问题分解成 n 个规模较小,并且结构与原问题相似的子问题,递归的解决这些子问题,然后合并结果就得到原问题的解。
从定义看,分治有些类似递归,但区别在于,分治算法是一种处理问题的思想,而递归是一种编程技巧。实际上,分治算法一般都适合用递归实现,分治算法中的递归实现中,每一层递归都会涉及以下三个操作:
- 分解:将原问题分解成一系列子问题
- 解决:递归的求解各个子问题,若问题足够小则直接求解
- 合并:将子问题的结果合并成原问题的结果
分治算法能解决的问题一般需要满足以下几个条件:
- 原问题与分解成的小问题具有相同的模式
- 原问题分解成的子问题可以独立求解,子问题之间没有相关性
- 具有分解终止条件,也就是说,当问题足够小时,可以直接求解
- 可以将子问题合并成原问题,而这个合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果
分治代码模板
- terminator
- process(split your big problem)
- drill down (subproblmes)
- merge(subresult)
- reverse states
public void divide_conquer(Problem problem, String... params) {
// 终止条件 recursion terminator
if (problem == null) {
// process_result
return;
}
// 准备数据、问题拆分 prepare data
data = prepare_data(problem) ;
subproblems = split_problem(problem, data);
// 下探下一层,分别处理子问题 conquer subproblems
subresult1 = divide_conquer(subproblem[0], p1);
subresult2 = divide_conquer(subproblem[1], p1);
subresult3 = divide_conquer(subproblem[2], p1);
// 结果合并 process and generate the final result
result = process_result(subresult1, subresult2, subresult3, …);
// 清理当前层 revert the current level status
}
回溯(backtracking)
回溯的处理思想,有点类似枚举搜索。枚举所有的解,找到满足期望的解。为了有规律地枚举所有可能的解,避免遗漏和重复,我们把问题求解的过程分为多个阶段。每个阶段,都会面对一个岔路口,我们先随意选一条路走,当发现这条路走不通的时候(不符合期望的解),就回退到上一个岔路口,另选一种走法继续走。
回溯法通常采用最简单的递归方法实现,在反复重复以上步骤枚举解后可能出现两种情况:
- 找到一个可能存在的正确答案
- 在尝试了所有可能的分步方法后宣告该问题没有解
在最坏情况下,回溯法会导致一次复杂度为指数时间的计算。
典型应用:
- 八皇后问题
- 0-1 背包
- 正则表达式
LeetCode实战
50. Pow(x, n)
实现 pow(x, n) ,即计算 x 的 n 次幂函数。
示例 1:
输入: 2.00000, 10
输出: 1024.00000
示例 2:
输入: 2.10000, 3
输出: 9.26100
示例 3:
输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25
说明:
- -100.0 < x < 100.0
- n 是 32 位有符号整数,其数值范围是 [−2^31, 2^31 − 1] 。
题解:
「快速幂算法」的本质是分治算法。举个例子,要计算 x^64,我们可以按照以下顺序:
x -> x^2 -> x^4 -> x^8 -> x^16 -> x^32 -> x^64
// 1. 快速幂 + 递归
// 时间复杂度:O(log n),即为递归的层数;
// 空间复杂度:O(logn)
class Solution {
public double quickMul(double x, long N) {
if (N == 0) {
return 1.0;
}
double y = quickMul(x, N / 2);
return N % 2 == 0 ? y * y : y * y * x;
}
public double myPow(double x, int n) {
long N = n;
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}
}
// 2. 快速幂 + 迭代
// 时间复杂度:O(logn),即为对 n 进行二进制拆分的时间复杂度。
// 空间复杂度:O(1)。
class Solution {
double quickMul(double x, long N) {
double ans = 1.0;
// 贡献的初始值为 x
double x_contribute = x;
// 在对 N 进行二进制拆分的同时计算答案
while (N > 0) {
if (N % 2 == 1) {
// 如果 N 二进制表示的最低位为 1,那么需要计入贡献
ans *= x_contribute;
}
// 将贡献不断地平方
x_contribute *= x_contribute;
// 舍弃 N 二进制表示的最低位,这样我们每次只要判断最低位即可
N /= 2;
}
return ans;
}
public double myPow(double x, int n) {
long N = n;
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}
}
78. 子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
递归:
开始假设输出子集为空,每一步都向子集添加新的整数,并生成新的子集。
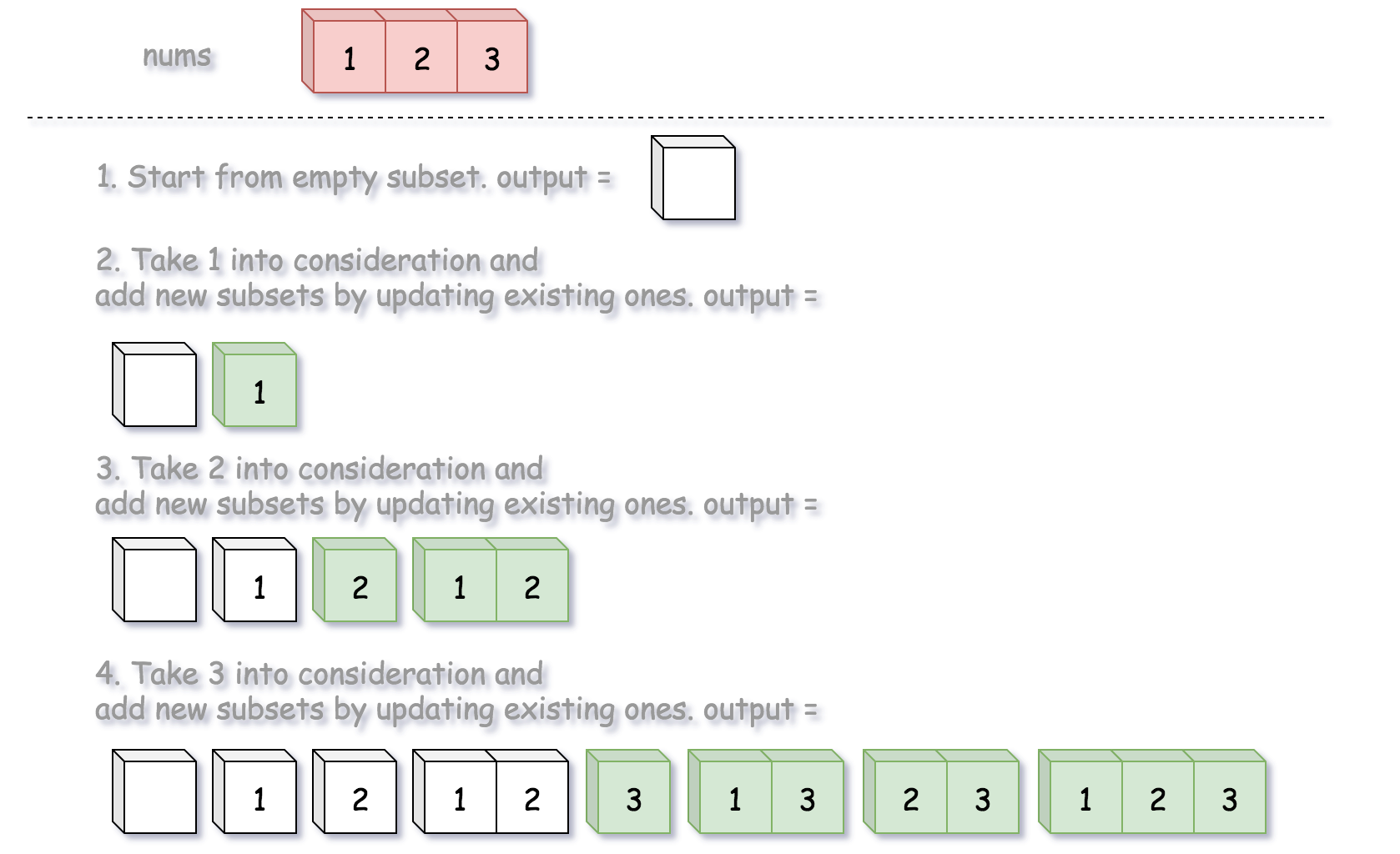
回溯:
根据定义,该问题可以看作是从序列中生成幂集。遍历 子集长度,通过 回溯 生成所有给定长度的子集。
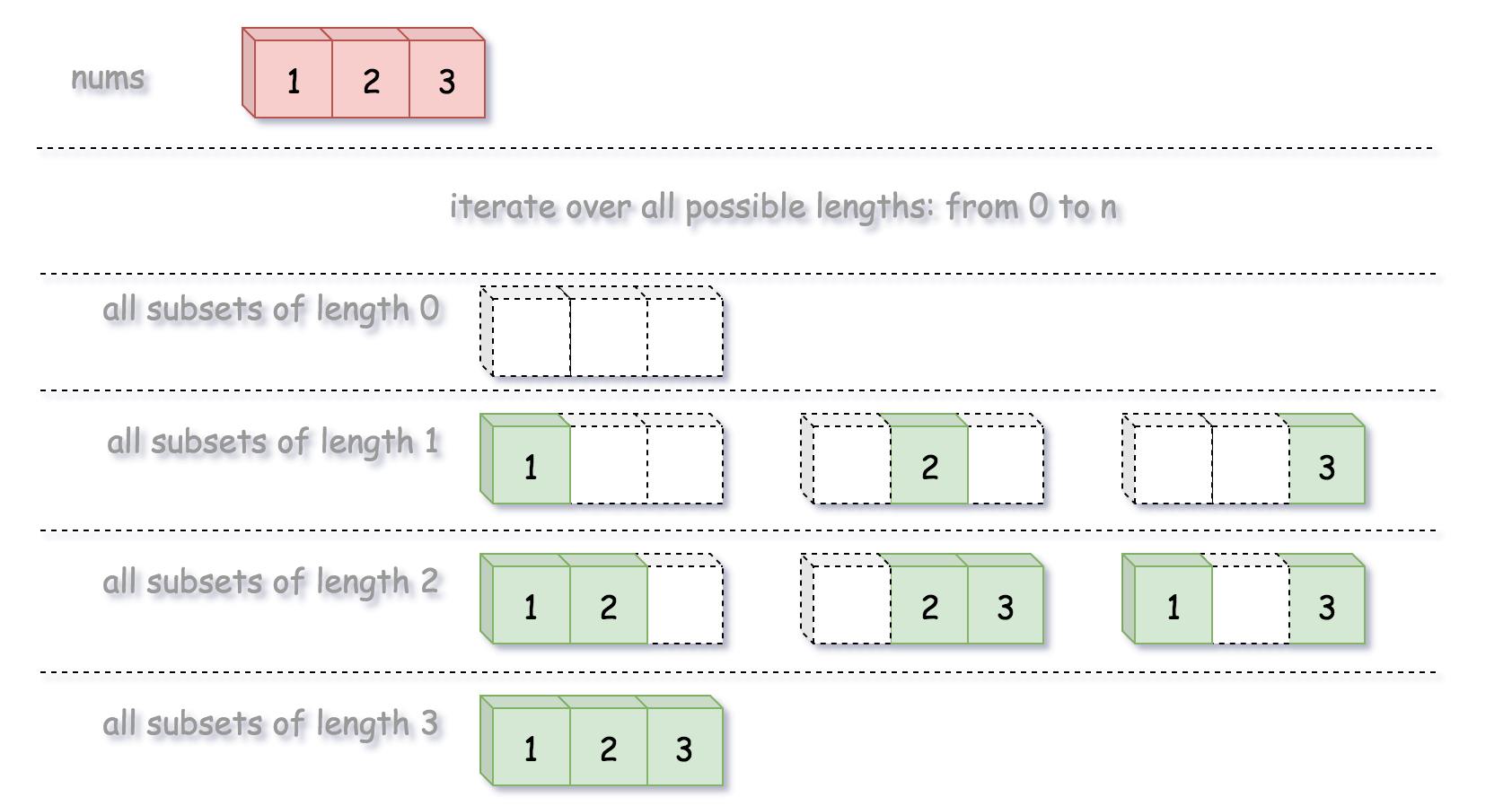
![]()
// 1. 递归
// 时间复杂度:O(N * 2^N)
// 空间复杂度:O(N * 2^N)
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> output = new ArrayList();
output.add(new ArrayList<Integer>());
for (int num : nums) {
List<List<Integer>> newSubsets = new ArrayList();
for (List<Integer> curr : output) {
newSubsets.add(new ArrayList<Integer>(curr){{add(num);}});
}
for (List<Integer> curr : newSubsets) {
output.add(curr);
}
}
return output;
}
}
// 2. 回溯
// 时间复杂度:O(N * 2^N)
// 空间复杂度:O(N * 2^N)
class Solution {
List<List<Integer>> output = new ArrayList();
int n, k;
public void backtrack(int first, ArrayList<Integer> curr, int[] nums) {
// if the combination is done
if (curr.size() == k)
output.add(new ArrayList(curr));
for (int i = first; i < n; ++i) {
// add i into the current combination
curr.add(nums[i]);
// use next integers to complete the combination
backtrack(i + 1, curr, nums);
// backtrack
curr.remove(curr.size() - 1);
}
}
public List<List<Integer>> subsets(int[] nums) {
n = nums.length;
for (k = 0; k < n + 1; ++k) {
backtrack(0, new ArrayList<Integer>(), nums);
}
return output;
}
}
参考文献:
- 数据结构与算法之美-王争
- 算法训练营-覃超
- LeetCode


 浙公网安备 33010602011771号
浙公网安备 33010602011771号