数据结构与算法（Ⅰ）： 复杂度分析&数组、链表、跳表

衡量不同算法之间的优劣主要是从算法所占用的「时间」和「空间」两个维度考量，即：

• 时间维度：指执行当前算法所消耗的时间，通常用「时间复杂度」描述。
• 空间维度：指执行当前算法需要占用多少内存空间，通常用「空间复杂度」描述。

时间复杂度

时间复杂度通过运行程序验证所消耗时间时，受运行环境、数据规模等因素影响差异很大，因此使用通用表示法描述时间复杂度。例如，大O符号表示法，即T(n) = O(f(n))，表示代码执行时间随数据规模增长的变化趋势，也叫作渐进时间复杂度（asymptotic time complexity）。

常见时间复杂度量级（按量级递增）

1. 常数阶O(1)
2. 线性阶O(n)
3. 对数阶O(logn)、线性对数阶O(nlogn)
4. 平方阶O(n^{2)、立方阶O(n}3)、k次方阶O(n^k)
5. 指数阶O(2^n)
6. 阶乘阶O(n!)

• O(1)

int i = 2; 
int j = 4; 
int sum = i + j;

• O(logn)、O(nlogn)

i=1; 
while (i <= n) { 
    i = i * 2; 
    // i = i * 3;
}

• O(m+n)、O(m*n)

int cal(int m, int n) { 
    int sum_1 = 0; 
    for (int i = 1; i < m; ++i) { 
        sum_1 = sum_1 + i; 
    } 
    
    int sum_2 = 0; 
    for (int j = 1; j < n; ++j) { 
        sum_2 = sum_2 + j; 
    } 
    
    return sum_1 + sum_2;
}

从代码中可以看出，m 和 n 是表示两个数据规模。我们无法事先评估 m 和 n 谁的量级大，所以我们在表示复杂度的时候，就不能简单地利用加法法则，省略掉其中一个。
所以，上面代码的时间复杂度就是 O(m+n)。针对这种情况，原来的加法法则就不正确了，我们需要将加法规则改为：T1(m) + T2(n) = O(f(m) + g(n))。
但是乘法法则继续有效：T1(m)*T2(n) = O(f(m) * f(n))。

空间复杂度

空间复杂度全称是渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系。
空间复杂度是对算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。常用的有：O(1)、O(n)、O(n²)。

数组

数组(Array)是由相同类型的元素集合(element)所组成的数据结构，由一块连续内存存储。利用元素的索引(index)可以计算出该元素对应的存储地址。

一维（或单维）数组是一种线性数组，内存连续, 其中元素的访问是以行或列索引的单一下标表示。查询复杂度O(1), 添加/删除时，向索引为index的地方添加/删除元素，index之后的元素都需要向后移动，所以需要进行n次操作即O(n)，向末尾只需进行一次操作即O(1)。

二维数组，多维数组，都属于非线性结构。

链表

链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而顺序表相应的时间复杂度分别是O(logn)和O(1)。

单向链表

一个单向链表的节点被分成两个部分。第一个部分保存或者显示关于节点的信息，第二个部分存储下一个节点的地址。单向链表只可向一个方向遍历。

双向链表

“双向链表”或“双面链表”是一种更复杂的链表。每个节点有两个连接：一个指向前一个节点，（当此“连接”为第一个“连接”时，指向空值或者空列表）；而另一个指向下一个节点，（当此“连接”为最后一个“连接”时，指向空值或者空列表）

双向链表也叫双链表。双向链表中不仅有指向后一个节点的指针，还有指向前一个节点的指针。这样可以从任何一个节点访问前一个节点，当然也可以访问后一个节点，以至整个链表。一般是在需要大批量的另外储存数据在链表中的位置的时候用。

循环链表

循环链表中, 首节点和末节点被连接在一起。这种方式在单向和双向链表中皆可实现。

块状链表

块状链表本身是一个链表，但是链表储存的并不是一般的数据，而是由这些数据组成的顺序表。每一个块状链表的节点，也就是顺序表，可以被叫做一个块。

块状链表通过使用可变的顺序表的长度和特殊的插入、删除方式，可以在达到O(√n)的复杂度。块状链表另一个特点是相对于普通链表来说节省内存，因为不用保存指向每一个数据节点的指针。

跳表

跳跃列表使得包含n个元素的有序序列的查找和插入操作的平均时间复杂度都是O(logn)，优于数组的O(n)复杂度。

跳跃列表通过维护一个多层次的链表实现，且与前一层（下面一层）链表元素的数量相比，每一层链表中的元素的数量更少（如下图）。开始时，算法在最稀疏的层次进行搜索，直至需要查找的元素在该层两个相邻的元素中间。这时，算法将跳转到下一个层次，重复刚才的搜索，直到找到需要查找的元素为止。跳过的元素的方法可以是随机性选择或确定性选择，其中前者更为常见。

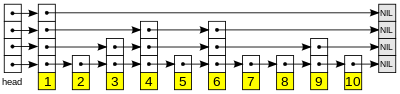
（跳跃列表的示意图。每个带有箭头的框表示一个指针, 而每行是一个稀疏子序列的链表；底部的编号框（黄色）表示有序的数据序列。查找从顶部最稀疏的子序列向下进行, 直至需要查找的元素在该层两个相邻的元素中间。）

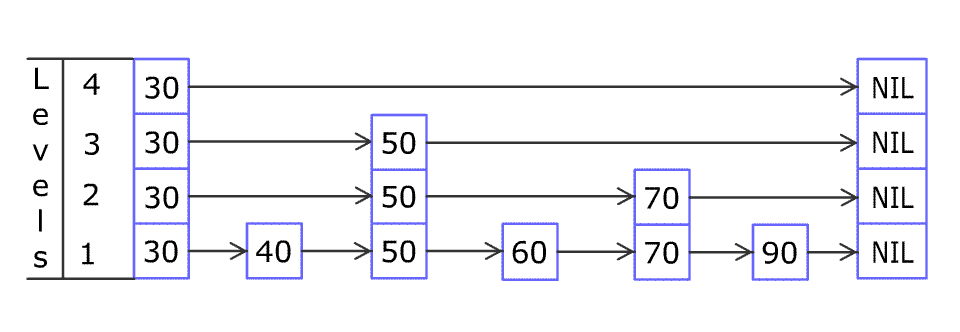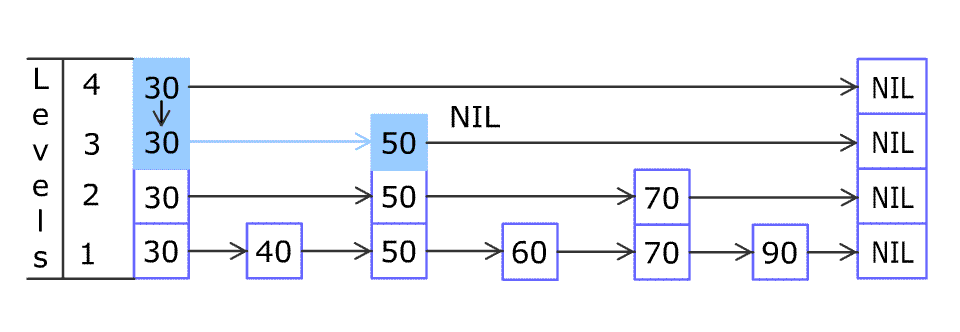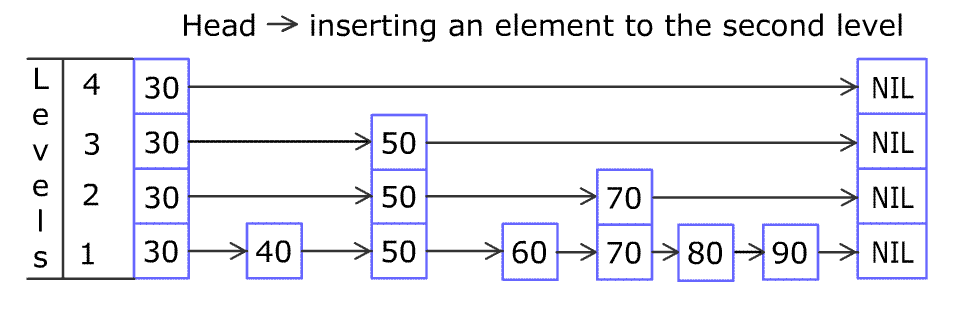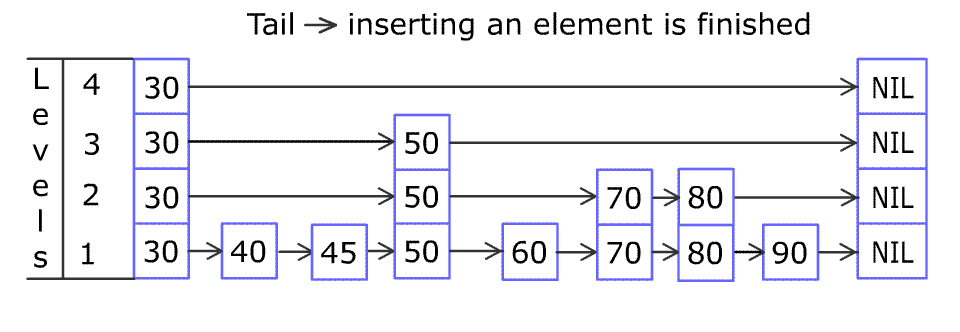
（向跳跃列表中插入一个元素）

LeetCode实战

283. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

输入: [0,1,0,3,12]

输出: [1,3,12,0,0]

说明:

必须在原数组上操作，不能拷贝额外的数组。
尽量减少操作次数。

// 思路：设置一个index，表示非0数的个数，循环遍历数组，
// 如果不是0，将非0值移动到第index位置,然后index + 1
// 遍历结束之后，index值表示为非0的个数，再次遍历，从index位置后的位置此时都应该为0

public void moveZeroes(int[] nums) {
	if (nums == null || nums.length <= 1) {
		return;
	}
	
	int index = 0;
	for (int i = 0; i < nums.length; i++) {
		if (nums[i] != 0) {
			nums[index] = nums[i];
			index++;
		}
	}

	for (int i = index; i < nums.length; i++) {
		nums[i] = 0;
	}
}

11. 盛最多水的容器

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点(i,ai) 。在坐标内画 n 条垂直线，垂直线 i的两个端点分别为(i,ai) 和 (i, 0)。找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且n的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为49。

示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

// 1. 暴力法 枚举 O(n^2)
public int maxArea(int[] height) {
		
	int max = 0;
	for (int i = 0; i < height.length; i++) {
		for (int j = i + 1; j < height.length; j++) {
			int area = (j - i) * Math.min(height[i], height[j]);
			max = Math.max(max, area);
		}
	}

	return max;
}
	
// 2. 双指针法 左右边界收敛 O(n)
public int maxArea(int[] height) {

	int max = 0;
	for (int i = 0, j = height.length -1; i < j; ) {
		int minHeight = height[i] < height[j] ? height[i++] : height[j--];
		int area = (j - i + 1) * minHeight;
		max = Math.max(max, area);
	}

	return max;
}

70. 爬楼梯

假设你正在爬楼梯。需要 n阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶
   示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

// 用f(n)表示爬到第n级台阶的方案数，考虑最后一步可能跨了一级台阶，也可能跨了两级台阶，爬到第n级台阶的方案数是爬到第n-1级台阶的方案数和爬到第n-2级台阶的方案数的和。
// f(n) = f(n-1) + f(n-2) 
// O(n)
	
public int climbStairs(int n) {

	if (n <= 2) {
		return n;
	}

	int one_step_before = 2;
	int two_steps_before = 1;
	int all_ways = 0;

	for(int i = 2; i < n; i++){
		all_ways = one_step_before + two_steps_before;
		two_steps_before = one_step_before;
		one_step_before = all_ways;
	}

	return all_ways;
}

1. 两数之和

给定一个整数数组 nums和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

// 1. 暴力解 O(n^2)
public int[] twoSum(int[] nums, int target) {

    for(int i = 0; i < nums.length - 1; i++) {
        for(int j = i + 1; j < nums.length; j++) {
            if(nums[i] + nums[j] == target) {
                return new int[] { i, j };
            }
        }
    }
    
    return new int[2];
}

// 2. 两遍哈希表 O(n)
public int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        map.put(nums[i], i);
    }
    
    for (int i = 0; i < nums.length; i++) {
        int complement = target - nums[i];
        if (map.containsKey(complement) && map.get(complement) != i) {
            return new int[] { i, map.get(complement) };
        }
    }
    
    return new int[2];
}

// 3. 一遍哈希表 O(n)
public int[] twoSum(int[] nums, int target) {

    Map<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        int complement = target - nums[i];
        if (map.containsKey(complement)) {
            return new int[] { map.get(complement), i };
        }
        map.put(nums[i], i);
    }
    
     return new int[2];
}

15. 三数之和（高频老题）

给你一个包含 n 个整数的数组nums，判断nums中是否存在三个元素 a，b，c ，使得a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例：

给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：

[
  [-1, 0, 1],
  [-1, -1, 2]
]

解题思路：

• 暴力法搜索为 O(N^3) 时间复杂度，可通过双指针动态消去无效解来优化效率。
• 双指针法铺垫： 先将给定 nums 排序，复杂度为 O(NlogN)。
• 双指针法思路： 固定 3 个指针中最左（最小）数字的指针 k，双指针 i，j 分设在数组索引 (k, len(nums))(k,len(nums)) 两端，通过双指针交替向中间移动，记录对于每个固定指针 k 的所有满足 nums[k] + nums[i] + nums[j] == 0 的 i,j 组合：
  1. 当 nums[k] > 0 时直接break跳出：因为 nums[j] >= nums[i] >= nums[k] > 0，即 33 个数字都大于 00 ，在此固定指针 k 之后不可能再找到结果了。
  2. 当 k > 0且nums[k] == nums[k - 1]时即跳过此元素nums[k]：因为已经将 nums[k - 1] 的所有组合加入到结果中，本次双指针搜索只会得到重复组合。
  3. i，j 分设在数组索引 (k, len(nums))(k,len(nums)) 两端，当i < j时循环计算s = nums[k] + nums[i] + nums[j]，并按照以下规则执行双指针移动：
     • 当s < 0时，i += 1并跳过所有重复的nums[i]；
     • 当s > 0时，j -= 1并跳过所有重复的nums[j]；
     • 当s == 0时，记录组合[k, i, j]至res，执行i += 1和j -= 1并跳过所有重复的nums[i]和nums[j]，防止记录到重复组合。

复杂度分析：

• 时间复杂度 O(N^2)：其中固定指针k循环复杂度 O(N)，双指针 i，j 复杂度 O(N)。
• 空间复杂度 O(1)：指针使用常数大小的额外空间。

// 1. 暴力解 O(n^3)
private List<List<Integer>> directlySolution(int[] nums) {
    if (nums == null || nums.length <= 2) {
        return Collections.emptyList();
    }
    
    Arrays.sort(nums);
    Set<List<Integer>> result = new LinkedHashSet<>();
    
    for (int i = 0; i < nums.length; i++) {
        for (int j = i + 1; j < nums.length; j++) {
            for (int k = j + 1; k < nums.length; k++) {
                if (nums[i] + nums[j] + nums[k] == 0) {
                    List<Integer> value = Arrays.asList(nums[i], nums[j], nums[k]);
                    result.add(value);
                }
            }
        }
    }

    return new ArrayList<>(result);
}

// 2. 哈希表 O(n^2)
private List<List<Integer>> hashSolution(int[] nums) {
    if (nums == null || nums.length <= 2) {
        return Collections.emptyList();
    }
    
    Set<List<Integer>> result = new LinkedHashSet<>();

    for (int i = 0; i < nums.length - 2; i++) {
        int target = -nums[i];
        Map<Integer, Integer> hashMap = new HashMap<>(nums.length - i);
        for (int j = i + 1; j < nums.length; j++) {
            int v = target - nums[j];
            Integer exist = hashMap.get(v);
            if (exist != null) {
                List<Integer> list = Arrays.asList(nums[i], exist, nums[j]);
                list.sort(Comparator.naturalOrder());
                result.add(list);
            } else {
                hashMap.put(nums[j], nums[j]);
            }
        }
    }

    return new ArrayList<>(result);
}

// 3. 排序+双指针 O(n^2)
public List<List<Integer>> threeSum(int[] nums) {
    Arrays.sort(nums);
    List<List<Integer>> res = new ArrayList<>();
    
    for(int k = 0; k < nums.length - 2; k++){
    
        if(nums[k] > 0) break;
        if(k > 0 && nums[k] == nums[k - 1]) continue;
        
        int i = k + 1, j = nums.length - 1;
        
        while(i < j){
            int sum = nums[k] + nums[i] + nums[j];
            
            if(sum < 0){
                while(i < j && nums[i] == nums[++i]);
            } else if (sum > 0) {
                while(i < j && nums[j] == nums[--j]);
            } else {
                res.add(new ArrayList<Integer>(Arrays.asList(nums[k], nums[i], nums[j])));
                while(i < j && nums[i] == nums[++i]);
                while(i < j && nums[j] == nums[--j]);
            }
        }
    }
    
    return res;
}

Linked List

206. 反转链表

24. 两两交换链表中的节点

141. 环形链表*

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
 
// 1. 暴力解 O(n)
public boolean hasCycle(ListNode head) {
    Set<ListNode> nodesSeen = new HashSet<>();
    while (head != null) {
        if (nodesSeen.contains(head)) {
            return true;
        } else {
            nodesSeen.add(head);
        }
        head = head.next;
    }
    return false;
}

// 2. 快慢指针 O(n)
// 慢指针每次移动一步，而快指针每次移动两步。如果列表中不存在环，最终快指针将会最先到达尾部，此时我们可以返回 false。
public boolean hasCycle(ListNode head) {
    if (head == null || head.next == null) {
        return false;
    }
    ListNode slow = head;
    ListNode fast = head.next;
    while (slow != fast) {
        if (fast == null || fast.next == null) {
            return false;
        }
        slow = slow.next;
        fast = fast.next.next;
    }
    return true;
}
        

142. 环形链表 II

25. K 个一组翻转链表

参考文献：

• 算法训练营-覃超
• 算法图解
• 维基百科
• LeetCode