数字逻辑课本习题一
一、单选题
- 以下代码中为位权码的是( )。
A)余3循环码 B) 5211码 C)余3码 D)右移码
【知识点】
二——十进制编码有多种不同的编码方法，也就是说有多种不同的BCD码，常用的有 8421BCD码、2421BCD码、5211BCD码、余3码、余3格雷码等。
其中8421码、2421码、5211码都属于位权码，即编码中每1位对应一个位权值，如8421BCD码中，各位的位权依次是8、4、2、1，编码1001对应的十进制数符是8+0+0+1=9。
余3码是由二进制码加3(0011)后形成的，即余3码从二进制码的3开始编码。余3格雷码是由格雷码加3后形成的，即余3格雷码从格雷码的3(0010)开始编码。
- 一位八进制数可以用( )位二进制数来表示。
A) 1 B) 2 C) 3 D) 4
- 十进制数43用8421BCD码表示为( )。
A) 10011 B) 0100 0011 C) 1000011 D) 101011
【注】
用4位二进制数对十进制数中的10个数符进行编码，简称二——十进制编码，又称BCD码(Binary Coded Decimal) 。
- A+BC= ( )。
A) AB+AC B) ABC C) (A+B)(A+C) D) BC
【注】
该题为定理中的分配律。
- -7的4位二进制补码数为( )。
A) 0111 B) 1111 C) 1000 D) 1001
- 在函数F(A, B, C, D) = AB + CD的真值表中，F=1的状态有( )。
A) 2个 B) 4个 C) 6个 D) 7个
- 已知2输入逻辑变量AB和输出结果Y的真值表如表1-30所示，则AB的逻辑关系为 ( )。
A)同或 B)异或 C)与非 D)或非
- 利用约束项化简逻辑函数时，约束项应看成( )。
A) 1 B) 2 C)能使圈组大的看成1，其他看成0 D)无所谓
- 当逻辑函数有$n$个变量时，共有( )组变量取值组合。
A) $n$ B) $2n$ C)${n^2}$ D) ${2^n}$
- 利用卡诺图化简逻辑函数时，8个相邻的最小项可消去( )个变量。
A) 1 B) 2 C) 3 D) 4
- 将图1-48所示的卡诺图化简，应画( )个包围圈。
A) 2 B) 3 C)4 D) 5
【画包围圈原则】
（1）包围圈中只能包围那些值为1的最小项，每个包围圈中只能包含 ${2^n}$ 个最小项。
（2）包围圈应尽可能大，这样才能消去更多变量，使对应的乘积项表达式简单。
（3）包围圈的数量应尽可能少，这样才能使最终的表达式中或运算最少。
（4）最小项可重复被圈，但应保证每一个圈中至少有一个新的、未被包围的最小项。
（5）画完包围圈后，应反复检查，去掉多余的包围圈。为避免重复画圈，画包围圈时，应尽可能从只有较少合并方式的最小项圈起。
（2）包围圈应尽可能大，这样才能消去更多变量，使对应的乘积项表达式简单。
（3）包围圈的数量应尽可能少，这样才能使最终的表达式中或运算最少。
（4）最小项可重复被圈，但应保证每一个圈中至少有一个新的、未被包围的最小项。
（5）画完包围圈后，应反复检查，去掉多余的包围圈。为避免重复画圈，画包围圈时，应尽可能从只有较少合并方式的最小项圈起。
- 卡诺图中，变量的取值按( )规律排列。
A) ASCII码 B) 8421BCD 码 C)余3码 D)格雷码
- 4变量逻辑函数的真值表，表中的输入变量的取值应有( )种。
A) 2 B) 4 C) 8 D) 16
- *TTL逻辑电路是以( )为基础的集成电路。
A)三极管 B)二极管 C)场效应管 D)晶闸管
- *CMOS逻辑电路是以( )为基础的集成电路。
A)三极管 B) NMOS管 C) PMOS管 D) NMOS管和PMOS管
二、判断题
- 十进制数 ${(64.5)_{10}}$。与十六进制数 ${(40.8)_{16}}$ 等值。
- 在任一输入为1的情况下，“或非”运算的结果是逻辑0。
- 逻辑变量的取值，1比0大。×
- 4位二进制数补码，1101比1100大。
- 4位二进制数原码，1101比1100大。×
- 如果 $A+B=A+C$，则 $B=C$。×
- 十进制数 ${(5)_{10}}$比十六进制数 ${(5)_{16}}$ 小。×
- 若两个逻辑函数具有不同的表达式，则两个逻辑函数必然不相等。×
- 若两个逻辑函数具有不同的真值表，则两个逻辑函数必然不相等。
- 函数 $F(A,B,C,D)$ 中，最小项 $A\overline B CD$ 对应的最小项编号是 ${m_{13}}$。×
【注】
重点理解记忆1~4个变量逻辑函数的卡诺图。
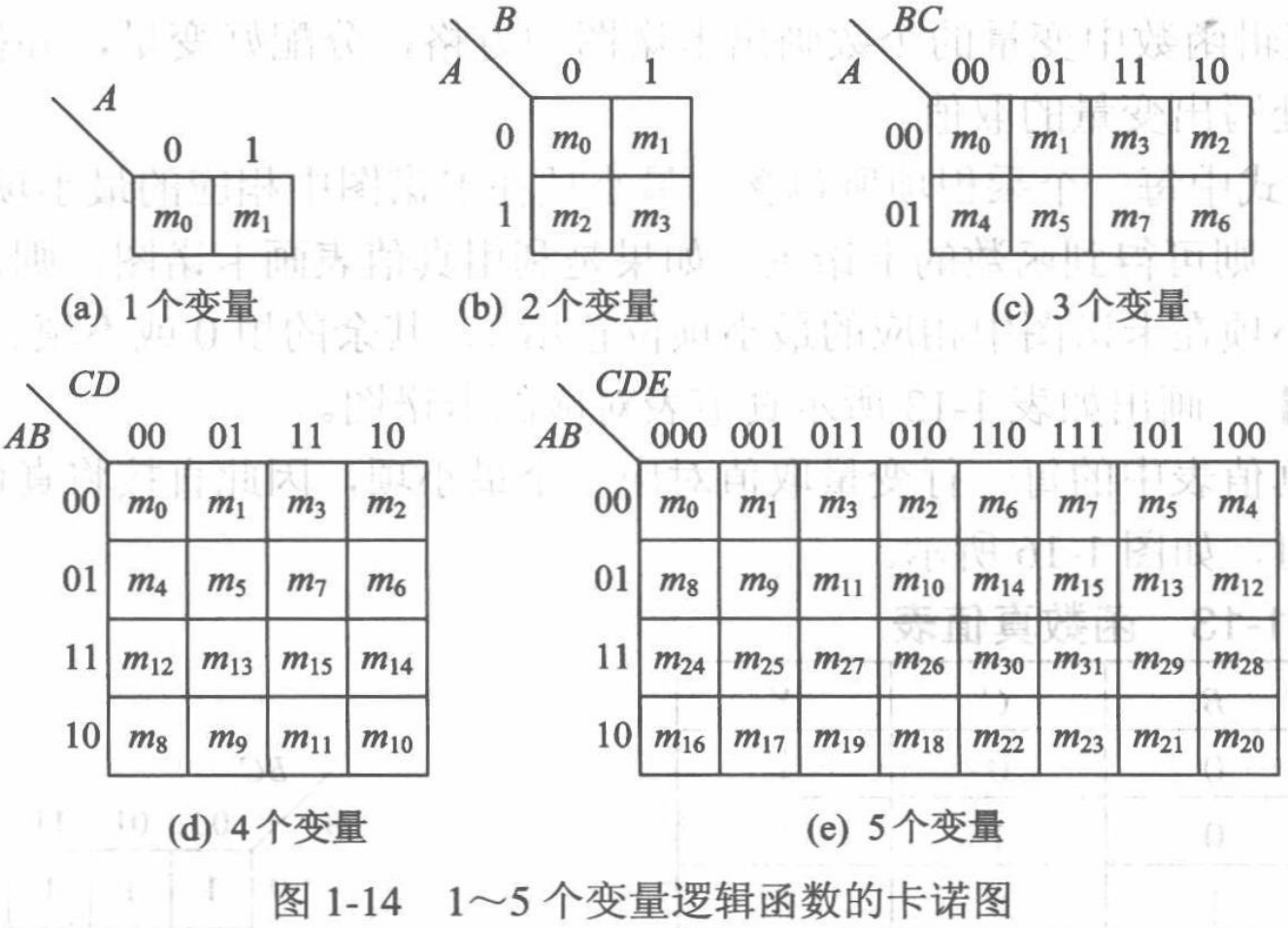
三、填空题
- $135.625 = 10000111.101{_2} = 207.5{_8} = 87.A{_{16}}$
- $10111001.11{_2} = 185.75{_{10}}$
- $94 = 10010100{_{8421BCD}}$
- 德・摩根定理是：
- $\overline {A + B} = \overline A \cdot \overline B $
- $\overline {A \cdot B} = \overline A + \overline B $
- 异或的定义为：$A \oplus B = A\overline B + \overline A B$
- 同或的定义为：$A \odot B = \overline A \overline B + AB$
- 逻辑表达式 $AB + A\overline C$ 对应的标准与或表达式是 $ ABC + AB\overline C + A\overline B \overline C $。
- 最简与或式 $AD + A\overline C$ 对应的最简与非——与非式是 $\overline {\overline {AD} \cdot \overline {A\overline C } } $ 。
- 函数 $Y = AB + \overline A \cdot \overline B $ 的反函数是 $A\overline B + \overline A B$。
- 某函数有 $n$ 个变量，则共有 ${2^n}$ 个最小项。
- 当 $ABCD$ 的值分别为 $1100$ 时，表达式 $AD + A\overline C + BC$ 的运算值为 $1$。
- 当 $ABCD$ 的值分别为 $1100$ 时，表达式 $A \oplus B \oplus C \oplus D \oplus 1$ 的运算值为 $1$。
