八、哈希表

常用术语

（1）同义词（Synonym）：哈希函数值相同的关键字称为同义词。

（2）冲突（Collision）：对不同的关键字可能得到同一哈希地址，即 $ke{y_1} \ne ke{y_2}$，而 $H(ke{y_1}) = H(ke{y_2})$。

（3）哈希函数和哈希地址（Hash function）：在记录的存储位置 $p$ 和其关键字 $key$ 之间建立一个确定的对应关系 $H$，使 $p=H(key)$，称这个对应关系 $H$ 为哈希函数，$p$ 为哈希地址。

（4）哈希表：一个有限连续的地址空间，用以存储按哈希函数计算得到相应散列地址的数据记录。通常哈希表的存储空间是一个一维数组，哈希地址是数组的下标。

 

哈希函数的构造方法

一、直接定址法

最简单的直接定址法（Direct addressing）直接用关键字 $key$ 作为哈希地址，即 $H(key)=key$。

虽然这种哈希函数简单，且不会产生冲突，但在实际应用中，关键字很少是连续的，采用这种特殊哈希函数会造成哈希表空间浪费。一般情况下，直接定址法可通过对关键字缩放和平移，获得合适的地址区间，即 $H(key) = a \times key + b$。其中，$a$ 为缩放系数，$b$ 为平移系数。

int hash_d(int key)
{
    return a*key+b;
}

二、除留余数法

假设哈希表表长为 $m$ ，除留余数法（Divided and get the remainder）选择一个不大于 $m$ 的数 $p$ 为模 ，用 $p$ 去除关键字，除后所得余数为哈希地址，即 $H(key)=key%p$。

这个方法的关键是选取适当的 $p$ ，一般情况下，可以选 $p$ 为小于表长的最大质数（素数）。例如，表长 $m=100$ ，可取 $p=97$ 。

int hash_m(int key)
{
    return key%p;
}

 

处理冲突的方法

一、链地址法

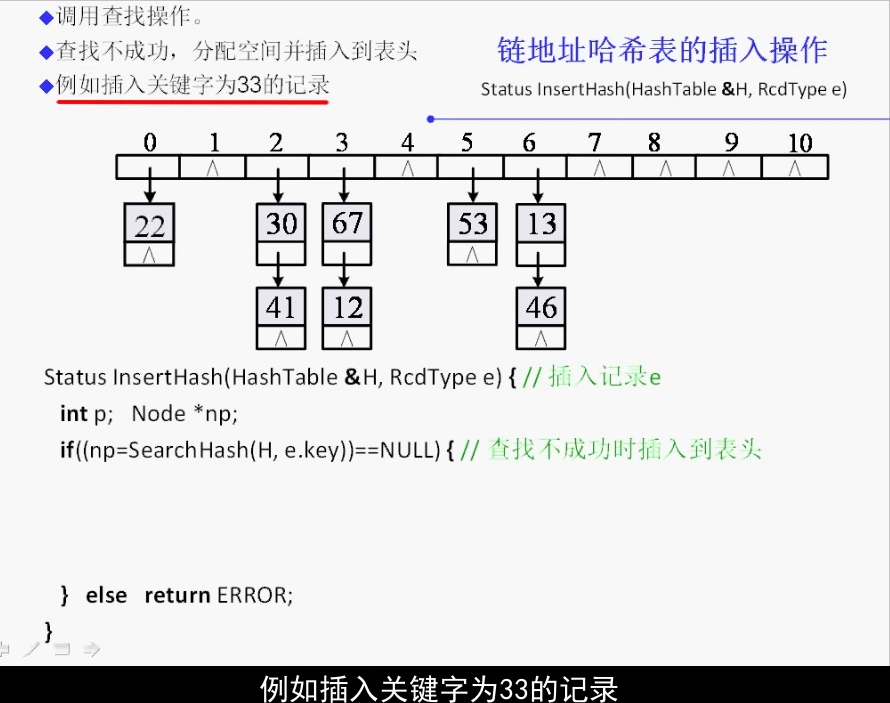
链地址法（Separate chaining）的基本思想是：把具有相同哈希地址的记录放在同一个单链表中，称为同义词链表。有 $m$ 个哈希地址就有 $m$ 个单链表，同时用数组 $HT[0...m - 1]$ 存放各个链表的头指针，凡是哈希地址为的记录都以结点方式插入到以 $HT[i]$ 为头结点的单链表中。

 

二、开放地址法

开放地址法（Open addressing）的基本思想是：把记录都存储在散列表数组中，当某一记录关键字 $key$ 的初始哈希地址为 ${H_0} = H(key)$ 发生冲突时，以 ${H_0}$ 为基础，采取合适方法计算得到另一个地址 ${H_1}$ ，如果 ${H_1}$ 仍然发生冲突，以 ${H_1}$ 为基础再求下一个地址 ${H_2}$ ，若 ${H_2}$ 仍然冲突，再求得 ${H_3}$ 。依次类推，直至 ${H_k}$ 不发生冲突为止，则以为该记录在表中的哈希地址。

这种方法在寻找“下一个”空的哈希地址时，原来的数组空间对所有的元素都是开放的，所以称为开放地址法。通常把寻找“下一个”空位的过程称为探测，上述方法可用如下公式表示：

${H_i} = (H(key) + {d_i})\% m$

其中，$H(key)$ 为哈希函数，$m$ 为哈希表表长，${d_i}$ 为增量序列。根据${d_i}$ 取值的不同，可以分为以下2种探测方法。

1. 线性探测法

当 ${d_i} = 0,1,2,...,m - 1$ 时，称为线性探测法（Linear Probing）。这种方法的特点是：冲突发生时，顺序查看表中下一个单元（探测到表尾地址 $m-1$ 时，下一个探测地址是表首地址0）, 直到找出一个空闲单元（当表未填满时一定能找到一个空闲单元）或查遍全表。

例如插入 $22,41,53,46,30,13,12,67$ ，哈希表表长为 $11$，哈希函数为 ${H_i} = H(key)\% 11$，如下图演示

线性探测法可能使第个哈希地址的同义词存入第个散列地址，这样本应存入第个散列地址的元素就争夺第个哈希地址的元素的地址，也就是说同义词冲突的探查序列和非同义词之间不同的探查序列交织在一起，从而造成大量元素在相邻的哈希地址上“聚集”（或堆积）起来，大大降低了查找效率。

 

2.平方探测法

平方探测法（Quadratic Probing）是消除线性探测中一次聚集问题的冲突解决方法。当 ${d_i} = {0^2},{1^2}, - {1^2},{2^2}, - {2^2},...,{k^2}, - {k^2}$ 时，称为平方探测法，其中 $k \le m/2$，哈希表长度 $m$ 必须是一个可以表示成 $4k+3$ 的素数，又称二次探测法。

平方探测法是一种处理冲突的较好方法，可以避免出现“堆积”问题，它的缺点是不能探测到哈希表上的所有单元，但至少能探测到一半单元。

 

哈希表的查找性能

查找过程中需和给定值进行比较的关键字的个数取决于三个因素：散列函数、处理冲突的方法和散列表的装填因子（Load Factor）。

哈希表的装填因子 $\alpha $ 定义为 $\alpha  = \frac{表中填入的记录数}{哈希表的长度}$

几种不同方法处理冲突时哈希表的平均查找长度