十六、二叉树（二叉链表）遍历算法

二叉树的遍历

遍历二叉树( Traversing binary tree )是指按某条搜索路径巡访树中每个结点，使得每个结点均被访问一次，而且仅被访问一次。

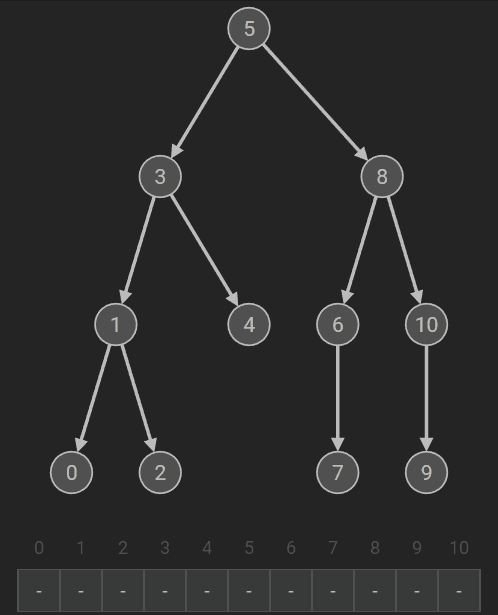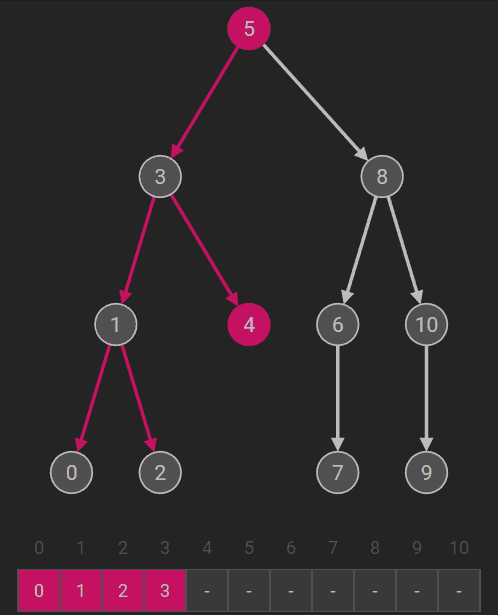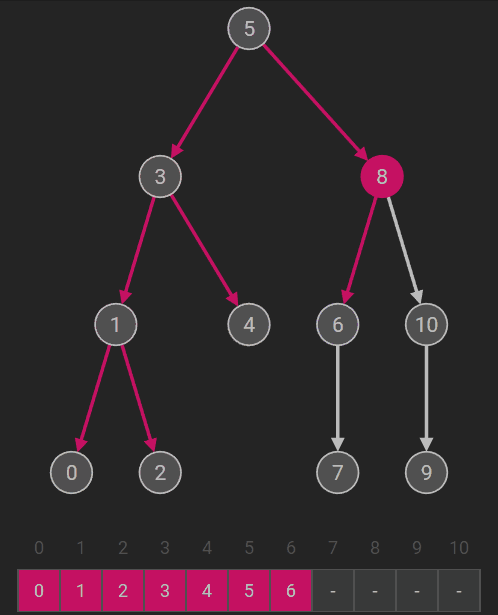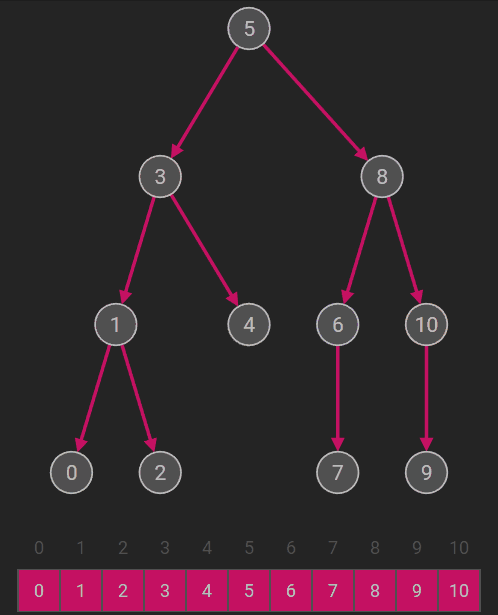
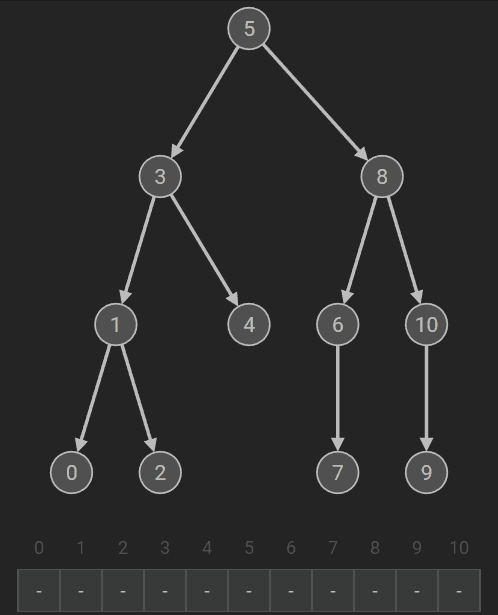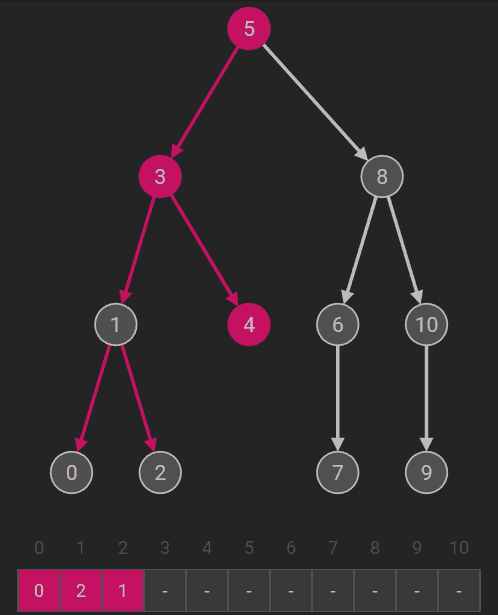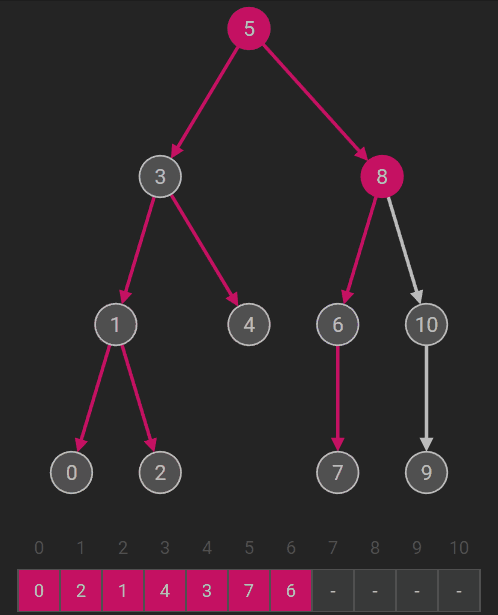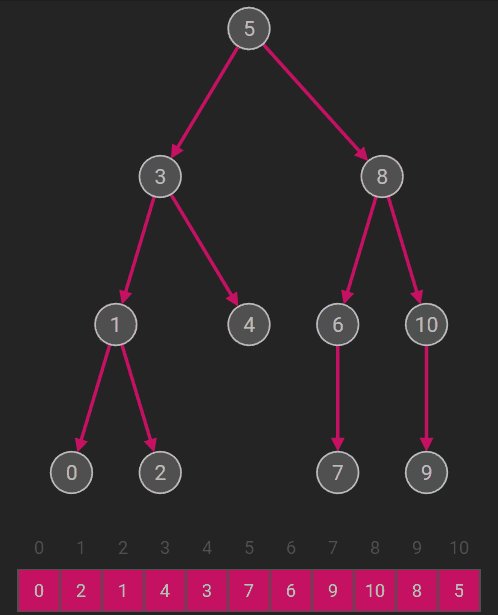
先序遍历（根左右）	中序遍历（左根右）	后序遍历（左右根）	层次遍历
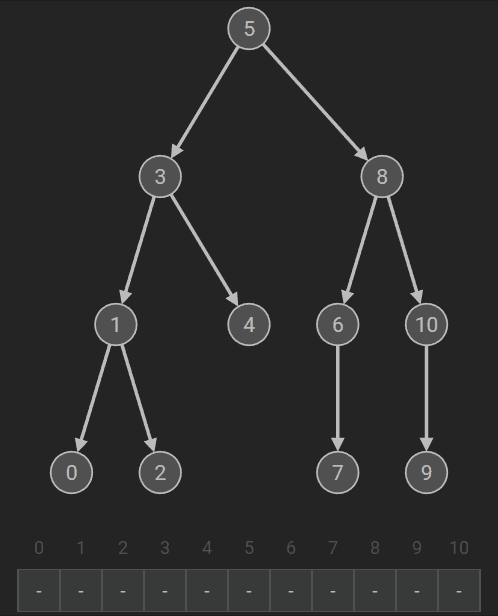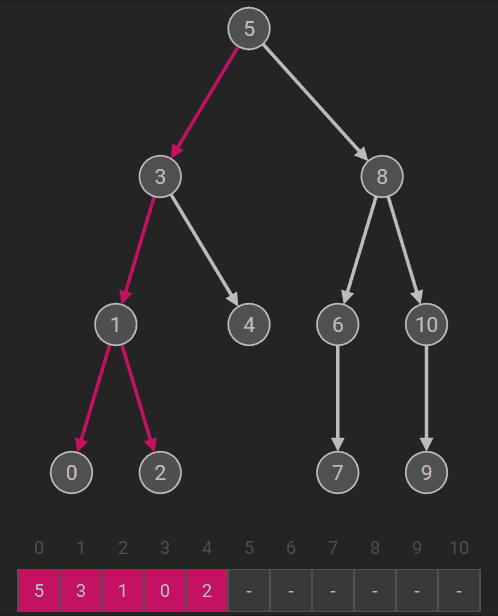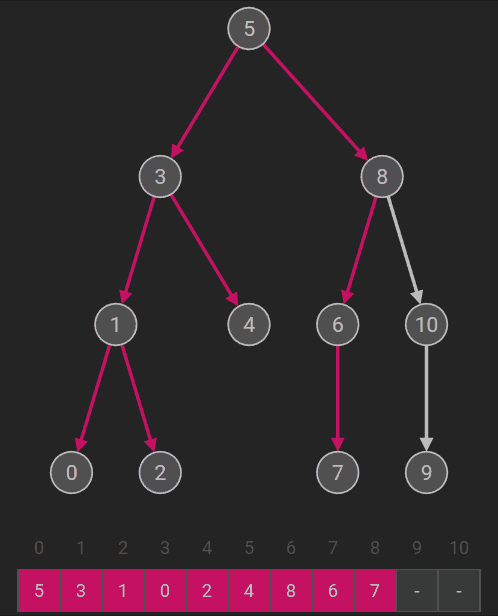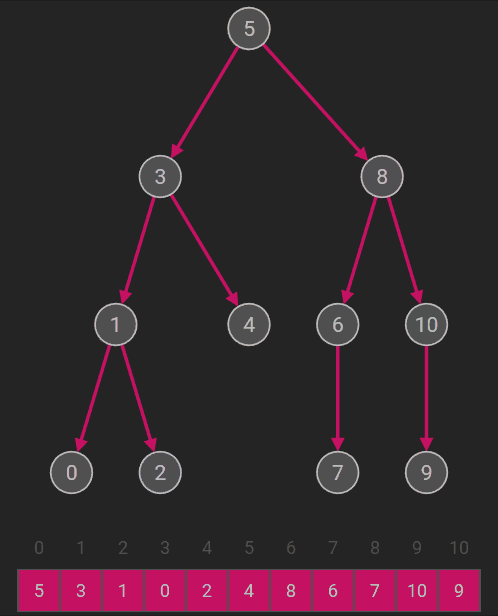
若二叉树为空，则空操作；否则 (1)访问根结点； (2)先序遍历左子树； (3)先序遍历右子树。	若二叉树为空，则空操作；否则 (1)中序遍历左子树； (2)访问根结点； (3)中序遍历右子树。	若二叉树为空，则空操作；否则 (1)后序遍历左子树； (2)后序遍历右子树； (3)访问根结点。	若二叉树为空，则空操作；否则 （1）访问根节点，将根节点入队; （2）当队列不为空是，重复以下操作。 1. 队头结点出队; 2. 若其有左孩子，则访问左孩子并入队; 3. 若其有右孩子，则访问右孩子并入队;

先序遍历递归算法

Status PreOrderTraverse(BiTree T, Status(*visit)(TElemType e))
{		//先序遍历二叉树T, visit是对数据元素操作的应用函数
	if (T == NULL) return OK;
    if (visit(T->data) == ERROR)
		return ERROR;							//(1)访问结点的数据域
	if (PreOrderTraverse(T->lchild, visit) == ERROR)
		return ERROR;							//(2)递归遍历T的左子树
	return PreOrderTraverse(T->rchild, visit);	//(3)递归遍历T的右子树
}

中序遍历递归算法

Status InOrderTraverse(BiTree T, Status(*visit)(TElemType e))
{		//中序遍历二叉树T, visit是对数据元素操作的应用函数
	if (T == NULL) return OK;
	if (InOrderTraverse(T->lchild, visit) == ERROR)
		return ERROR;							//(1)递归遍历T的左子树
	if (visit(T->data) == ERROR)
		return ERROR;							//(2)访问结点的数据域
	return InOrderTraverse(T->rchild, visit);	//(3)递归遍历T的右子树
}

后序遍历递归算法

Status PostOrderTraverse(BiTree T, Status(*visit)(TElemType e))
{		//中序遍历二叉树T, visit是对数据元素操作的应用函数
	if (T == NULL) return OK;
	if (PostOrderTraverse(T->lchild, visit) == ERROR)
		return ERROR;							//(1)递归遍历T的左子树
	if (PostOrderTraverse(T->rchild, visit) == ERROR)
		return ERROR;							//(2)递归遍历T的右子树
	return visit(T->data);	                    //(3)访问结点的数据域
}

例题

1. 设二叉树的先序遍历序列和后序遍历序列正好相反，则该二叉树满足的条件是（  B  ）。
A. 空或只有一个结点      B. 高度等于其结点数
C. 任一结点无左孩子      D. 任一结点无右孩子

【解析】只要二叉树中只有一个叶子结点（换句话说，就是高度等于其结点），即可满足先序遍历序列和后序遍历序列刚好相反。