三、排序基本概念和方法概述
一、排序的稳定性
当排序记录中的关键字 ${K_i}(i = 1,2,...,n)$ 都不相同时,则任何一个记录的无序序列经排序后得到的结果唯一;反之,当待排序的序列中存在两个或两个以上关键字相等的记录时,则排序所得的结果不唯一。
假设 ${K_i} = {K_j}(1 \le i \le n,1 \le j \le n,i \ne j)$ ,也就是说其对应的关键字相同,且在排序前的序列中 ${R_i}$ 领先于 ${R_j}$(即 $i<j$ )。若在排序后的序列中仍领先于,则称所用的排序方法是稳定的;反之,若可能使排序后的序列中领先于,则称所用的排序方法是不稳定的。注意,排序算法的稳定性是针对所有 记录而言的。也就是说,在所有的待排序记录中,只要有一组关键字的实例不满足稳定性要求,则该排序方法就是不稳定的。虽然稳定的排序方法和不稳定的排序方法排序结果不同,但不能说不稳定的排序方法就不好,各有各的适用场合。
例题
1. 排序算法的稳定性是指( A )。
A.经过排序后,能使关键字相同的元素保持原顺序中的相对位置不变
B.经过排序后,能使关键字相同的元素保持原顺序中的绝对位置不变
C.排序算法的性能与被排序元素个数关系不大
D.排序算法的性能与被排序元素的个数关系密切
二、排序算法的分类和基本原理
- 插入排序的原理:向有序序列中依次插入无序序列中待排序的记录,直到无序序列为空,对应的有序序列即为排序的结果,其主旨是“插入”。
- 交换排序的原理:先比较大小,如果逆序就进行交换,直到有序。其主旨是“若逆序就交换”。
- 选择排序的原理:从无序序列找关键字最小的记录,再放到已排好序的序列后面, 直到所有关键字全部有序,其主旨是“选择”。
- 归并排序的原理:依次对两个有序子序列进行“合并”,直到合并为一个有序序列为止,其主旨是“合并”。
- 基数排序的原理:接待排序记录的关键字的组成成分进行排序的一种方法,即依次比较各个记录关键字相应“位”的值进行排序,直到比较完所有的“位”,即得到一个有序的序列。
1. 直接插入排序
直接插入排序(Straight Insertion Sort)是一种最简单的排序方法,其基本操作是将一条记录插入到已排好序的有序表中,从而得到一个新的、记录数量增1的有序表。
算法步骤
- 设待排序的记录存放在数组 $r[1...n]$ 中,$r[1]$ 是一个有序序列。
- 循环 $n-1$ 次,每次使用顺序查找法,查找 $r[i] (i=2,...,n)$ 在已排好序的序列 $r[1...i-1]$ 中的插入位置,然后将 $r[i]$ 插入表长为 $i-1$ 的有序序列 $r[1...i-1]$,直到将$r[n]$ 插入表长为 $n-1$ 的有序序列 $r[1…n-1]$,最后得到一个表长为 $n$ 的有序序列。


算法
void Insertsort(RcdSqList& L) //对顺序表L作直接插入排序
{
int i, j;
for (i = 1; i < L.length; ++i)
{
if (L.rcd[i + 1].key < L.rcd[i].key) //需将 L.rcd[i+1]插入有序序列
{
L.rcd[0] = L.rcd[i + 1]; //先将记录L.rcd[ i+1]保存在空闲的0号单元
j = i + 1;
do{
j--;
L.rcd[j + 1] = L.rcd[j]; //记录后移
} while (L.rcd[0].key < L.rcd[j - 1].key); //判断是否需要继续移动
L.rcd[j] = L.rcd[0]; //插入(哨兵移动)
}
}
}
2. 希尔排序
希尔排序(Shell's Sort)又称“缩小增量排序”(Diminishing Increment Sort),是插入排序的一种。
算法步骤
希尔排序实质上是采用分组插入的方法。先将整个待排序记录序列分割成几组,从而减少参与直接插入排序的数据量,对每组分别进行直接插入排序,然后增加每组的数据量,重新分组。这样当经过几次分组排序后,整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
希尔对记录的分组,不是简单地“逐段分割”,而是将相隔某个“增量”的记录分成一组。
① 第一趟取增量 ${d_1}({d_1} < n)$ 把全部记录分成 ${d_1}$ 个组,所有间隔为 ${d_1}$ 的记录分在同一组,在各个组中进行直接插入排序。
② 第二趟取增量 ${d_2}({d_2} < {d_1})$ ,重复上述的分组和排序。
③ 依次类推,直到所取的增量 ${d_t} = 1({d_t} < {d_{t - 1}} < ... < {d_2} < {d_1})$,所有记录在同一组中进行直接插入排序为止。
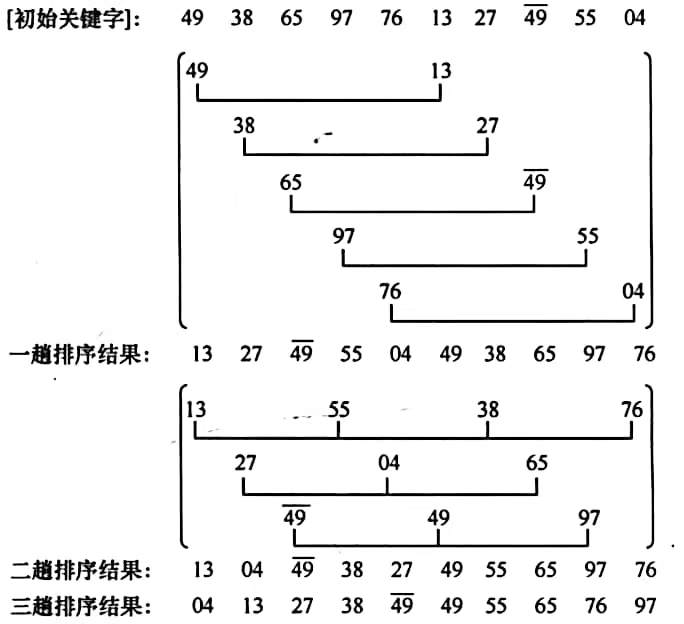
动图演示

3. 快速排序
快速排序(Quick Sort)是由冒泡排序改进而得的。
算法步骤
- 选择待排序表中的第一个记录作为枢轴,将枢轴记录暂存在r[0]的位置上。附设两个指针low和high,初始时分别指向表的下界和上界(第一趟时,low= 1; high = L.length;)。
- 从表的最右侧位置依次向左搜索,找到第一个关键字小于枢轴关键字pivotkey的记录,将其移到low处。具体操作是:当low<high时,若high所指记录的关键字大于等于pivotkey,则向左移动指针high (执行操作--high );否则将high所指记录移到low所指记录。
- 然后再从表的最左侧位置依次向右搜索,找到第一个关键字大于pivotkey的记录和枢轴记录交换。具体操作是:当low<high时,若low所指记录的关键字小于等于pivotkey,则向右移动指针low (执行操作++low );否则将low所指记录与枢轴记录交换。
- 重复步骤2和3,直至low与high相遇为止。此时low或high的位置即为枢轴在此趟排序中的最终位置,原表被分成两个子表。
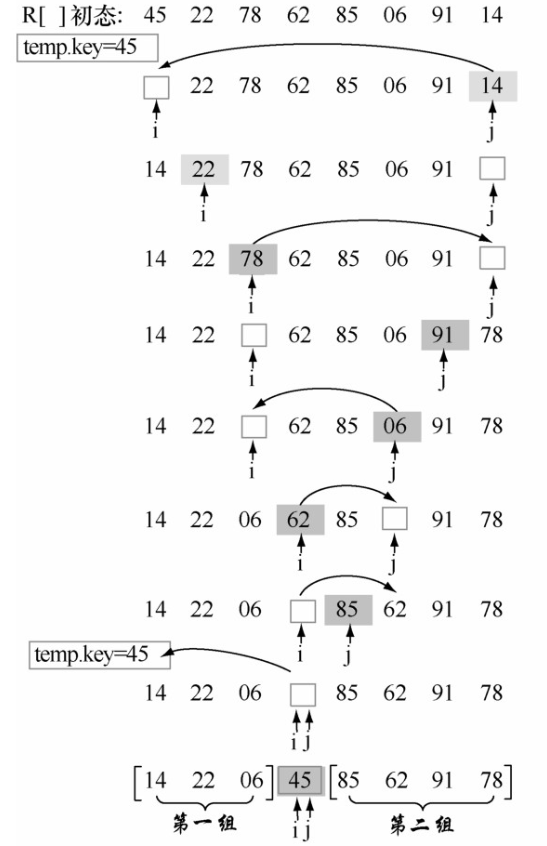
动图演示

算法
int Partition(RcdType rcd[], int low, int high)
{ //对子序列rcd[low ... high]进行一次划分,并返回枢轴应当所处的位置
//使得在枢轴之前的关键字均不大于它的关键字,枢轴之后的关键字均不小于它的关键字
rcd[0] = rcd[low]; //将枢轴移至数组的闲置单元
while (low < high) //只要low和high不相遇
{
while ( low < high && rcd[high].key >= rcd[0].key)
{
--high; //反复左移high
}
rcd[low] = rcd[high]; //将比枢轴关键字小的关键字移到低端
while (low < high && rcd[low].key <= rcd[0].key)
{
++low; //反复右移low
}
rcd[high] = rcd[low]; //将比枢轴关键字大的记录移到高端
}
rcd[low] = rcd[0]; //把rcd[0]放到low和high相遇的地方
return low; //返回相遇的下标
}
4. 基数排序
假设记录的逻辑关键字由 $d$ 个“关键字”组成,每个关键字可能取 $rd$ 个值。只要从最低数位关键字起,按关键字的不同值将序列中记录“分配”到 $rd$ 个队列中后再“收集”之,如此重复次完成排序。按这种方法实现排序称之为基数排序,其中“基”指的是 $rd$ 的取值范围。
具体实现时,一般采用链式基数排序。

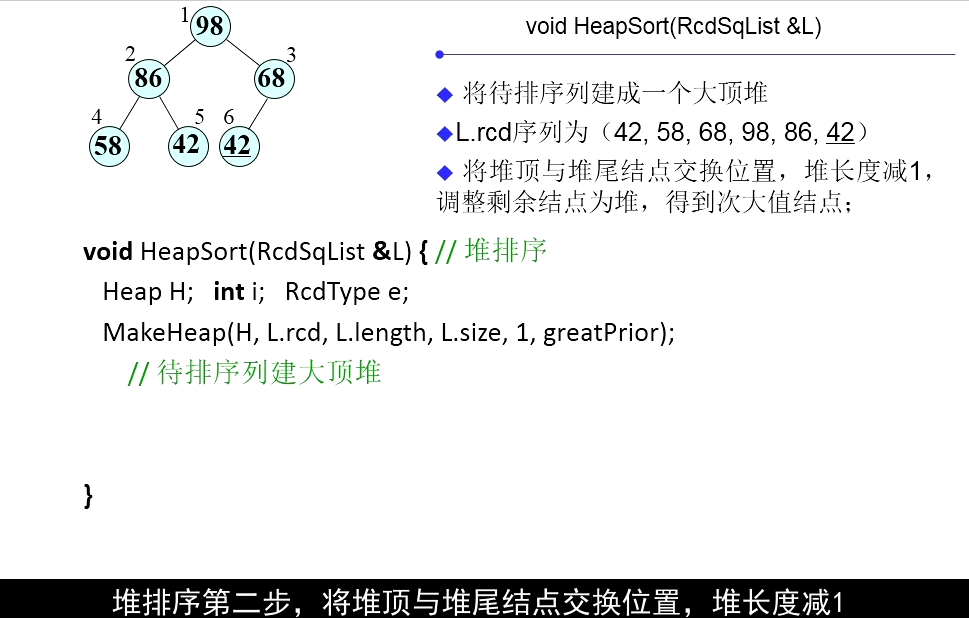
5. 堆排序