二、栈和队列
一、栈的定义和特点
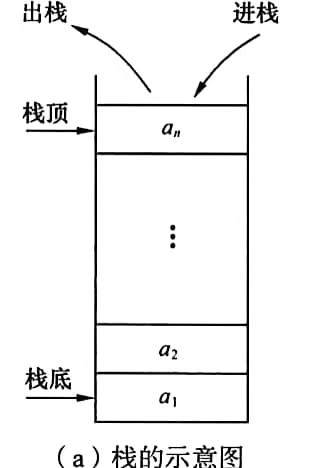
定义:栈(Stack)是(一种操作位置受限的线性结构)限定仅在表尾进行插入或删除操作的线性表。因此,对栈来说,表尾端有其特殊含义,称为栈顶(Top),相应地,表头端称为栈底(Bottom/Base)。不含元素的空表称为空栈。
特点:栈的操作是按后进先出(或称先进后出)的原则进行的,因此,栈又称为后进先出(Last In First Out, LIFO)的线性结构,或称先进后出(First In Last Out, FILO)的线性结构。
栈的常用操作(接口)包括:
Push (入栈 / 压入): insert new elem into stack
Pop (出栈 / 弹出): delete a elem from stackStatus InitStack_Sq(SqStack& S, int size, int inc); //初始化顺序栈 S
Status DestroyStack_Sq(SqStack& S); //销毁顺序栈 S
Status StackEmpty_Sq(SqStack S); //判断栈 S 是否空,若空则返回TRUE,否则返回FALSE
void ClearStack_Sq(SqStack& S); //清空栈S
Status Push_Sq(SqStack& S, ElemType e); //元素e压入栈S
Status Pop_Sq(SqStack& S, ElemType& e); //栈S的栈顶元素出栈,并用e返回
Status GetTop_Sq(SqStack S, ElemType& e); //取栈S的栈顶元素,并用e返回例题
1. 栈是( C )
| A. 顺序存储的线性结构 | B. 链式存储的非线性结构 |
| C. 限制存取点的线性结构 | D. 限制存储点的非线性结构 |
【解析】首先栈是一种线性表,所以B、D错。按存储结构的不同可分为顺序栈和链栈,但不可以把栈局限在某种存储结构上,所以A错。栈和队列都是限制存取点的线性结构。
2. 3个不同元素依次进栈,能得到( B )种不同的出栈序列。
| A. 4 | B. 5 | C. 6 | D. 7 |
【解析】
栈的数学性质: $n$ 个不同元素进栈,出栈元素不同排列的个数为 $\frac{1}{{n + 1}}C_{2n}^n$(卡特兰数)。
所以该题为$\frac{1}{{n + 1}}C_{2n}^n = \frac{1}{{n + 1}}\frac{{(2n)!}}{{n! \times n!}} = \frac{{6 \times 5 \times 4}}{{4 \times 3 \times 2 \times 1}} = 5$
3. 设 $a, b, c, d, e, f$ 以所给的次序进栈,若在进栈操作时,允许出栈操作,则下面得不到的序列为( D )。
| A. $fedcbd$ | B. $bcafed$ | C. $dcefba$ | D. $cabdef$ |
【解析】根据栈“先进后出”的特点,且在进栈操作的同时允许出栈操作,显然答案D中 $c$ 最先出栈,则此时栈内必定为 $a$ 和 $b$ ,但由于 $a$ 先于 $b$ 进栈,故要晚出栈。对于某个出栈的元素,在它之前进栈却晚出栈的元素必定是按逆序出栈的,其余答案均是可能出现的情况。此题也可采用将各序列逐个代入的方法来确定是否有对应的进出栈序。
二、队列的定义和特点
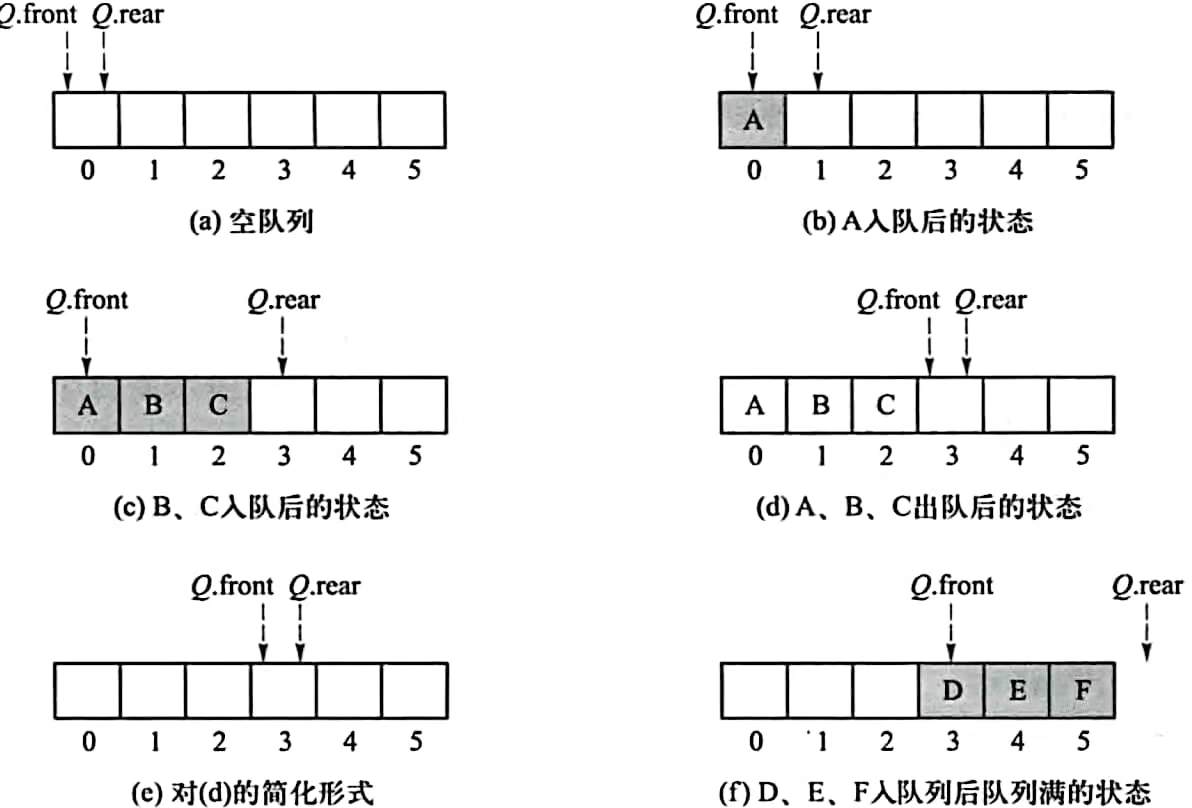
定义:队列(Queue)是一种先进先出(First In First Out, FIFO )的线性表。它只允许在表的一端进行插入,而在另一端删除元素。向队列中插入元素称为入队或进队;删除元素称为出队或离队。这和日常生活中的排队是一致的,最早进入队列的元素最早离开。在队列中,允许插入的一端称为队尾(Rear),允许删除的一端则称为队头(Front)。
栈的常用操作(接口)包括:
Status InitQueue_Sq(SqQueue& Q, int size); //构造一个空队列Q, 最大队列长度为size
Status DestroyQueue_Sq(SqQueue& Q); //销毁队列 Q, Q 不再存在
void ClearQueue_Sq(SqQueue& Q); //将 Q 置为空队列
Status QueueEmpty_Sq(SqQueue Q); //若队列 Q 为空队列则返回 TRUE,否则返回 FALSE
int QueueLength_Sq( SqQueue Q); //返回队列 Q 中元素个数,即队列的长度
Status GetHead_Sq(SqQueue Q, ElemType ae); //若队列不空,则用e返回Q的队列头元素,并返回0K;否则返回ERROR
Status EnQueue_Sq(SqQueue& Q, ElemType e); //在当前队列的尾元素之后插入元素e为新的队列尾元素
Status DeQueue_Sq(SqQueue& Q, ElemType& e); //若队列不空则删除当前队列Q中的头元素,用e返回其值,并返回0K;否则返回ERROR
循环队列
将顺序队列认为是一个环状的空间,即把存储队列元素的表从逻辑上视为一个环,称为循环队列(Circular Queue)。
假设少用一个元素空间,则有:
队空的条件(初始时):Q.front == Q.rear
队首指针进1:Q.front=(Q.front+1)%MaxSize
队尾指针进1:Q.rear=(Q.rear+1)%MaxSize
队满的条件:(Q.rear + 1)%MAXQSIZE == Q.front
队列的长度:(Q.rear-Q.front+MAXQSIZE)%MAXQSIZE
例题
1. 在循环队列中,若front与rear分别表示队头元素和队尾元素的位置,则判断循环队列空的条件是( C )。
| A. front == rear+1 | B. rear == front + 1 |
| C. front == rear | D. front == 0 |
【解析】
本题考查以顺序结构存储的循环队列的判空条件。注意题目的要求,front和rear指针分别指向队头和队尾元素,也就是说rear并没有我们说的指向队尾的下一个元素。真正做题的时候,我们要按照具体情况来分析。
front和rear指针分别指向队头和队尾元素时,循环队列为空,front=rear,故而选择C答案。
2. 若用一个大小为6的数组来实现循环队列,且当前rear和front的值分别为0和3,当从队列中删除一个元素,再加入两个元素后,rear和front的值分别为( B )。
| A. 1 和 5 | B. 2 和 4 | C. 4 和 2 | D. 5 和 1 |
3. 设数组Data[0, …, m]作为循环队列SQ的存储空间,front为队头指针,rear为队尾指针。其中,front指针指向队头元素,rear指针指向队尾元素的下一个位置。则执行出队操作 的语句为( A )。
| A. front = ( front + 1 ) % (m + 1) | B. front = ( front + 1 ) % m |
| C. rear = ( rear + 1 ) % m | D. front = front + 1 |
4. 循环队列存储在数组A[0...n]中,入队时的操作为( D )。
| A. rear = rear + 1 | B. rear = ( rear + 1 ) mod ( n - 1 ) |
| C. rear = ( rear + 1 ) mod n | D. rear = ( rear + 1 ) mod ( n + 1 ) |



