二十、树、森林和二叉树(二叉链表)转换
一、孩子兄弟表示法
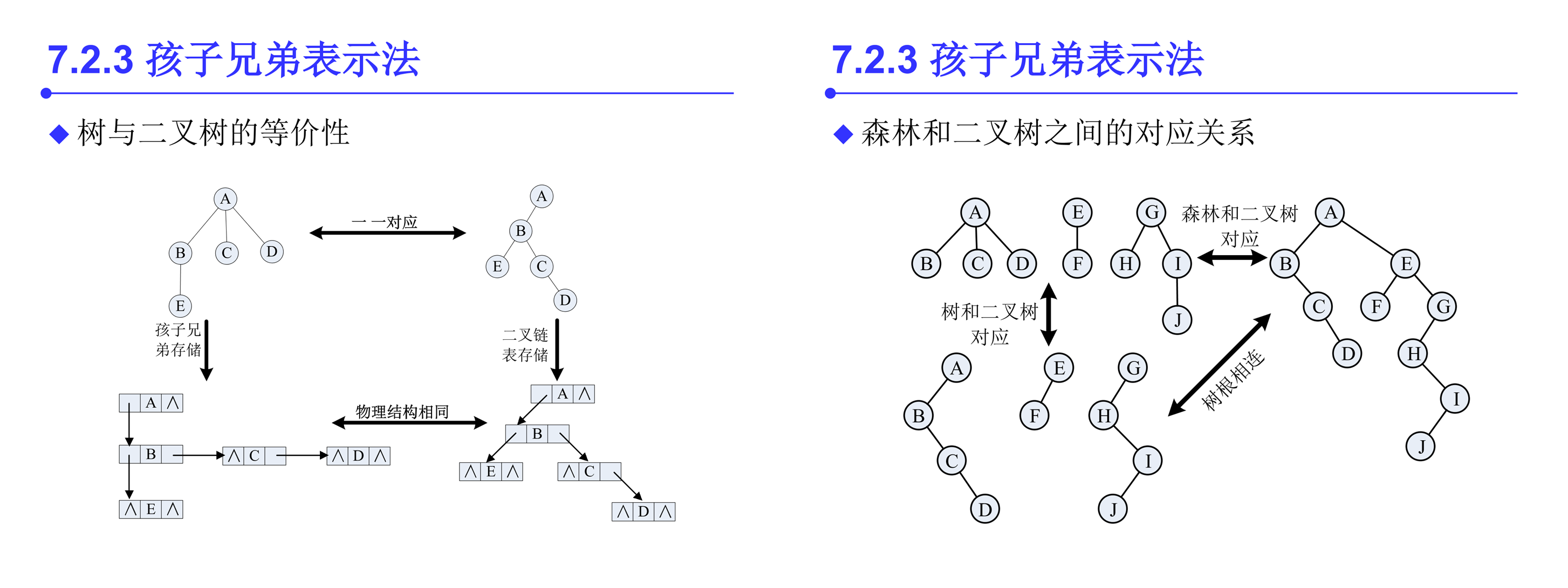
孩子兄弟表示法又称二叉树表示法,或二叉链表表示法,即以二叉链表做树的存储结构。链表中结点的两个链域分别指向该结点的第一个孩子结点和下一个兄弟结点,分别命名为firstchild域和nextsibling域。
// 树的二叉链表(孩子——兄弟)存储表示
typedef struct CSNode
{
ElemType data;
struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;二、树、森林和二叉树(二叉链表)转换
孩子兄弟表示法又称二叉树表示法,或二叉链表表示法,即以二叉链表做树的存储结构。链表中结点的两个链域分别指向该结点的第一个孩子结点和下一个兄弟结点,分别命名为firstchild域和nextsibling域。
从树的二叉链表表示的定义可知,任何一棵和树对应的二叉树,其根结点的右子树必空。若把森林中第二棵树的根结点看成是第一棵树的根结点的兄弟,则同样可导出森林和二叉树的对应关系。
树转换为二叉树的规则:每个结点左指针指向它的第一个孩子,右指针指向它在树中的相邻右兄弟,这个规则又称“左孩子右兄弟”。
将森林转换为二叉树的规则与树类似。先将森林中的每棵树转换为二叉树,由于任何一棵和对应的二叉树的右子树必空,若把森林中第二棵树根视为第一棵树根的右兄弟,即将第二棵树对应的二叉树当作第一棵二叉树根的右子树,将第三棵树对应的二叉树当作第二棵二叉树根的右子树……以此类推,就可以将森林转换为二叉树。
二叉树转换为森林的规则:若二叉树非空,则二叉树的根及其左子树为第一棵树含二叉树形式,故将根的右链断开。二叉树根的右子树又可视为一个由除第一棵树外的森林转换后的二叉树,应用同样的方法,直到最后只剩一棵没有右子树的二叉树为止,最后再将每棵二叉树依次转换成树,就得到了原森林,二叉树转换为树或森林是唯一的。
三、例题
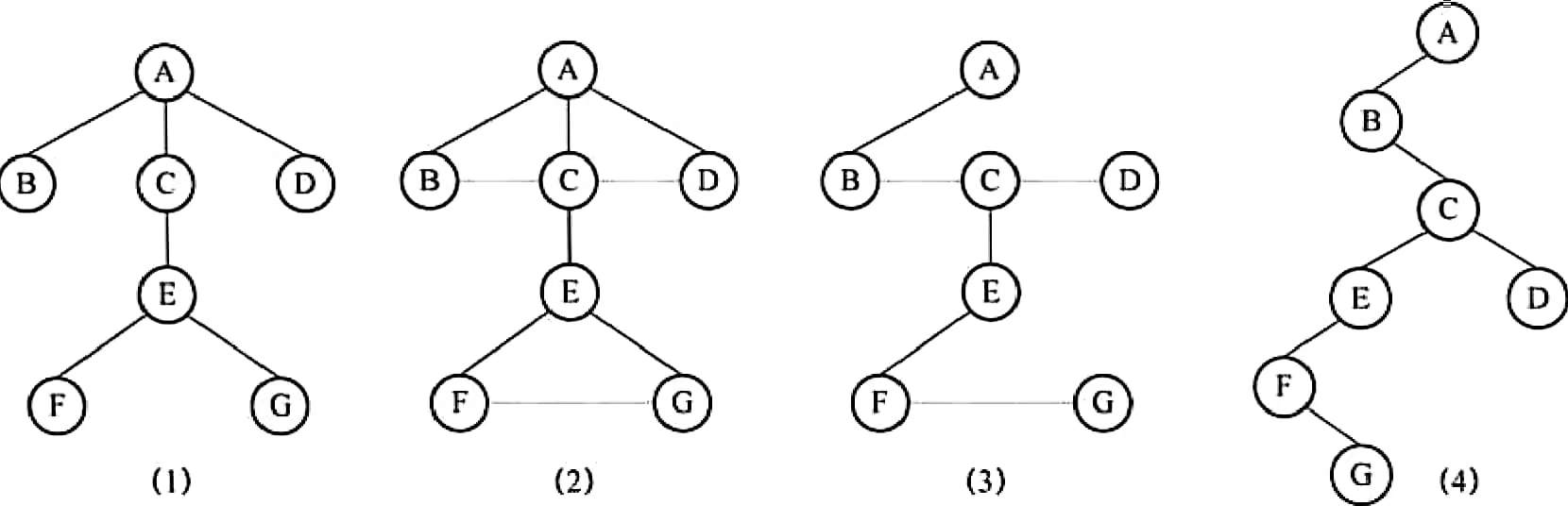
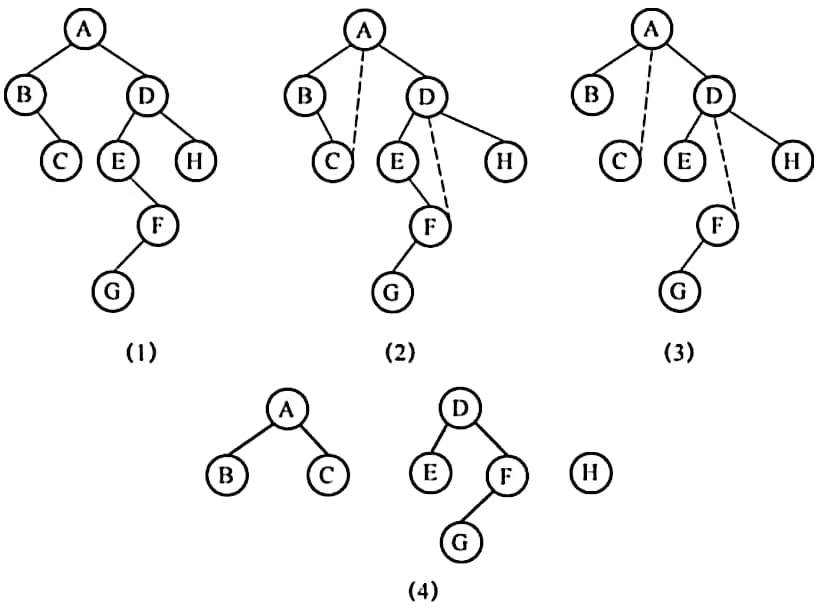
1.将图所示的树转换为二叉树,并写出该二叉树的先序遍历序列。

【解析】将一般树转化为二叉树的思路,主要根据树的孩子——兄弟存储方式而来,步骤如下。
(1)加线:即在各兄弟结点之间用虚线相连,可理解为每个结点的兄弟指针指向它的一个兄弟。
(2)抹线:对每个结点仅保留它与其最左一个孩子的连线,抹去该结点与其他孩子之间的连线(可理解为每个结点仅有一个孩子指针,让它指向自己的长子)。
(3)旋转:把虚线改为实线从水平方向向下旋转成右斜下方向,原树中实线成左斜下方向。这样,树就转换成二叉树了。
以图(2)~图(4)分别对应以上步骤。树转换得到了如图所示的二叉树。
该二叉树的先序遍历顺序为${A,B,C,E,F,G,D}$
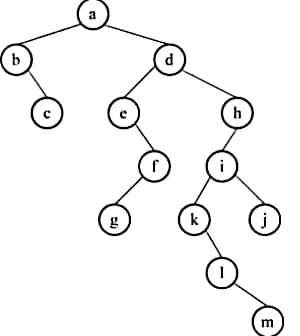
2.已知某森林的二叉树如图所示,试画出他所表示的森林。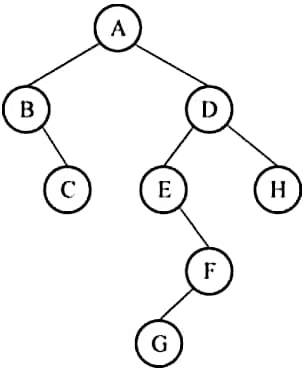
【解析】将二叉树还原成一般树,其还原过程也分为如下三步。
- 加线:若某结点 $i$ 是双亲结点的左孩子,则将该结点 $i$ 的右孩子以及当且仅当连续地沿着右孩子的右链不断搜索到所有右孩子,都分别与结点 $i$ 的双亲结点用虚线连接。
- 抹线:把原二叉树中所有双亲结点与其右孩子的连线抹去。这里的右孩子实质上是原一般树中结点的兄弟,抹去的连线是兄弟间的关系。
- 进行整理:把虚线改为实线,把结点按层次排列。
上面三个过程分别对应图(2)、(3)和(4),最后得到的二叉树如图(4)所示。
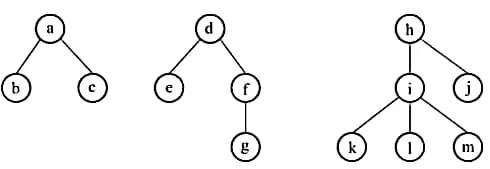
3. 将图所示的森林转换为二叉树
【解析】首先,将三棵树转换成二叉树,如下图所示
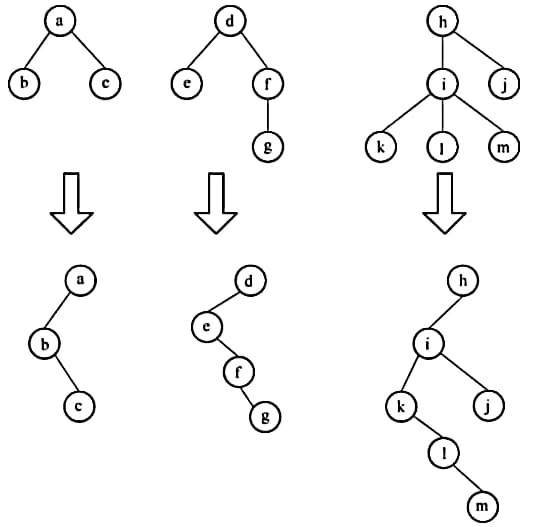
将这三棵二叉树合并成一棵二叉树,如下图所示