1.方法递归
1.1 简介
- 定义:方法自身调用方法自身就是递归。例如:
a(){
a();
}
- 举例:看如下代码即实现的是递归调用:
/* 方法递归 */ public class MethodDG { public static void main(String[] args) { System.out.println("main begin"); doSome(); System.out.println("main over"); } /*以下的代码片段虽然只有一份,但是可以被重复调用,并且只要调用doSome方法就会在栈内存中分配一块所属的内存空间 * */ public static void doSome() { System.out.println("begin"); doSome();//这行代码不结束,下一行程序是不能被执行的 System.out.println("over"); } }
以上的程序运行的时候肯定会发生如下错误:java.lang.StackOverflowError(这是错误不是异常),栈内存溢出错误,错误发生无法挽回,只有一个结果,就是 JVM 会停止工作。结论:
- 递归是很耗费栈内存的,递归算法可以不用的时候最好不用。
- 因此递归一定要有结束条件,如果没有结束条件,会发生栈内存溢出错误,但是即使结束条件是正确的,也可能会发生栈内存溢出错误,因为递归的太深了。
1.2 不使用递归,计算 1 ~ N 的和
- 第一种实现方式:
public class SumT1 { public static void main(String[] args) { int n = 5; int sum = 0; for (int i = 0; i <= n; i++) { sum = sum + i; } System.out.println(sum); } }
- 第二种:单独定义一个方法,作为独立功能,可以完成 1~ N 的求和:
public class SumT1 { public static void main(String[] args) { System.out.println(sum(5)); } public static int sum(int n){ int result = 0; for (int i=1;i<=n;i++){ result +=i; } return result; } }
1.3 使用递归计算 1~N 的求和
public class SumT2 { public static void main(String[] args) { System.out.println(sum(4)); } public static int sum(int n) { if (n==1){ return 1; } return n+sum(n-1); } }
我们分析下问什么按照以上代码即可以实现递归:
- 目标:求取 1 、2、3、4 这四个数字的和;
- 此时实现方式有如下两种方式:
- 第一种方式:1+2+3+4 正向进行相加
- 第二种方式:4+3+2+1 逆向进行相加
很明显我们应该采取第二种方式进行加和。还要注意递归的时候需要有结束条件,不然会发生栈内存溢出错误。所以我们第一步确认递归结束条件:如果 n==1,此时结束递归,将此时的值进行返回。
如果没有满足递归条件则此时按照如下计算逻辑进行计算:
-
- 4+sum(4-1)等价于 4+sum(3)
- sum(3) = 3+sum(2)
- sum(2) = 2+sum(1)
- sum(1) = 1
因此此时的递归逻辑应该是:4+3+2+1=10,即将我们需要的计算结果进行了返回。
1.4 计算 N 的阶乘
例如:5 的阶乘:5*4*3*2*1
- 通过非递归的方式实现
public class Factorial01 { public static void main(String[] args) { int n = 5; int retValue = method(n); System.out.println(retValue); } public static int method(int n) { int result = 1;//初始值为1 for (int i = n; i > 0; i--) {//此时的 i 的值依次为:5 4 3 2 1 result *= i; } return result; } }
执行结果为:120
- 通过递归的方式实现 N 的阶乘,本例中 N 取 5;
public class Factorial02 { public static void main(String[] args) { int n = 5; int retValue = method(n); System.out.println(retValue); } public static int method(int n){ int result = 1; if (n==1){ return 1; } return n*method(n-1); } }
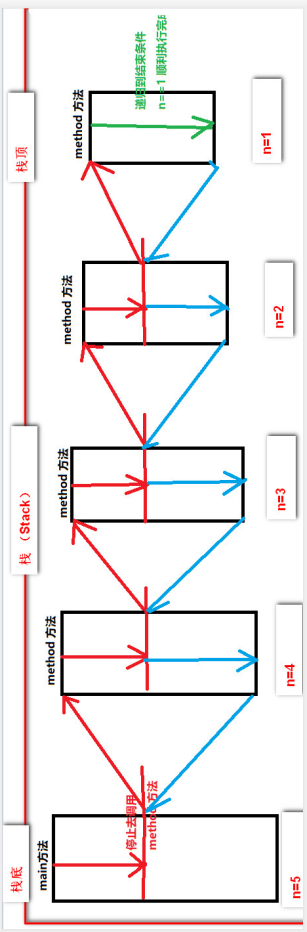
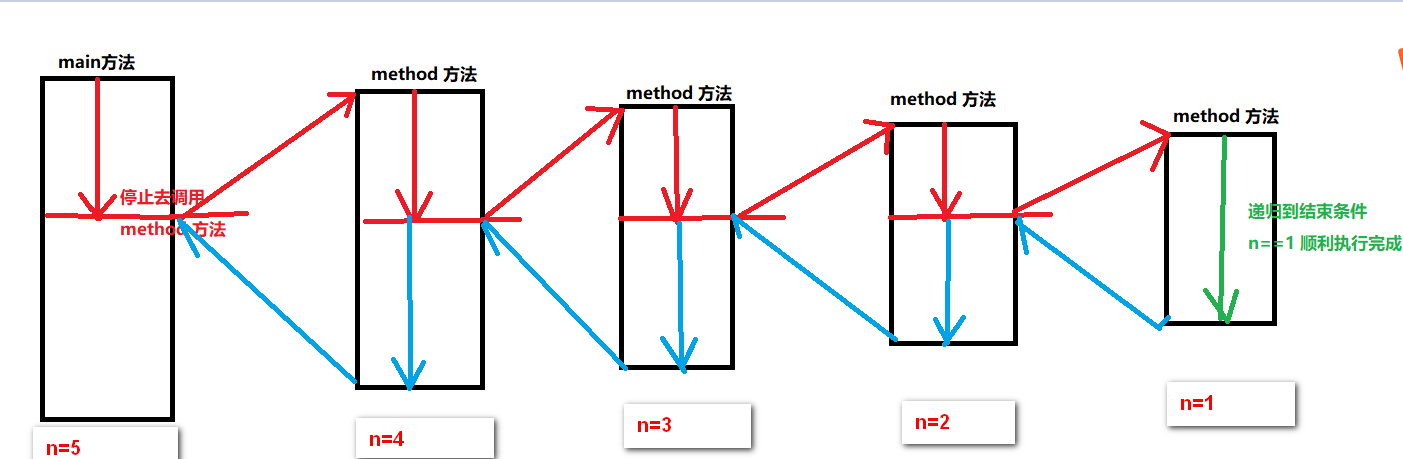
此时计算结果为:120如果我们用一个图来描述上述递归过程类似如下的调用过程:
我们将上述图逆时针旋转 90 度会发现,这其实就是一个栈,main 方法最先调用,但是处于栈底的位置,因此最后出结果,递归结束条件处于栈顶,因而最先出计算结果。